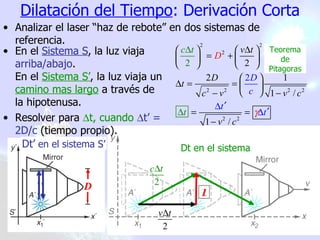
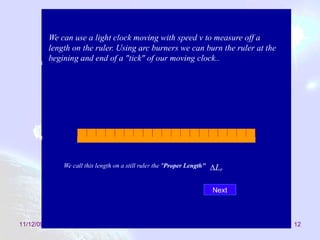
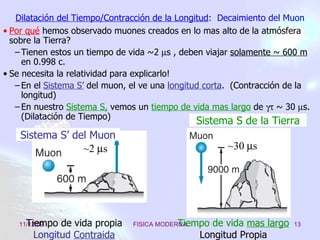
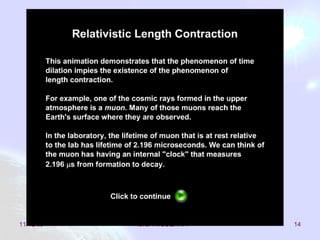
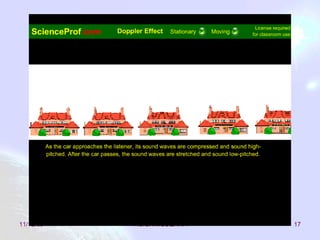
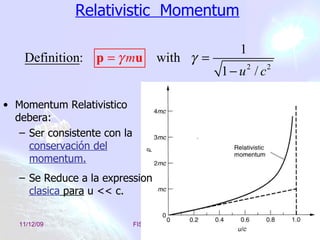
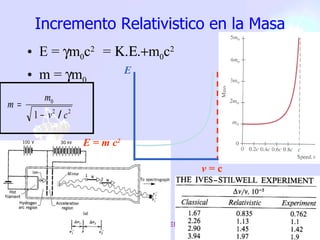
Este documento trata sobre la relatividad especial, incluyendo efectos como la dilatación del tiempo, la contracción de la longitud, la transformación de energía y momento, y las consecuencias de las transformaciones de Lorentz. El objetivo es estudiar estas consecuencias y comprender conceptos como la masa y el momento relativista.

1. RELATIVIDAD II

15. Dilatación del Tiempo/Contracción de la Longitud : Problema Domiciliario Una nave espacial parte desde la Tierra (v = 0.995c) hacia una estrella la cual esta a 100 años-luz .Encontrar cuanto le toma llegar respecto a alguien en la Tierra ( t 1 ) y a alguien en la nave espacial ( t 2 ) . Para t 2 , recordar que la nave espacial ve una distancia “contraria”  x’. Notar que alguien sobre la nave piensa que le toma solamente el 10% del tiempo en llegar a la estrellar como alquien en la Tierra cree tomarlo. Esto es porque vemos que el reloj en la nave “ corre mas lento ” comparado al reloj en la Tierra.

16. Efecto Doppler

19. Desplazamiento Doppler : Problema Domiciliario La luz desde una estrella cercana es observada para ser desplazada junto al rojo por 5% (f = 0.95 f o ). Esta la estrella acercandose o alejandose desde la Tierra? Cual es la rapidez de este movimiento? La estrella esta alejandose de la Tierra porque la frecuencia es desplazada a un valor muy bajo .

22. Warp 0.92 (0.75c) Relativity

29. Relativistic Energy : Definición & Ecuación“Simple” Energia TotalE = Energia cinetica K + Energia en reposo mc 2

31. Ecuación Invariante : Clasica vs. Relativistica Limite Clasico Limite muy Relativistico pc mc 2 E =  mc 2 E >> pc da E  mc 2 (   1)  K  ½ mu 2 or p 2 /2m E >> mc 2 da E  pc pc mc 2 E =  mc 2 Preciso hasta 1% o mejor si E > 8mc 2 Si K/mc 2  1%, entonces K aproximación con precisión hasta  1.5%.

32. 6 Variables dados por 5 Ecuac. (3 def., simple, cuadrado) Requiere mc 2 Requiere mc 2 Requiere mc 2 

33. Problema : Encontrar E, p, and K (dados u, mc 2 ) Encontrar la energ ia total E , momentum p (MeV/c), y energ ia cinetica K para un electron con masa en reposo 0.511 MeV y rapidez u = 0.5c . u da 

34. Problema : Encontrar pc y u (dados E, mc 2 ) Encontrar el momentum pc (MeV) y rapidez u de un electrón con masa en reposo 0.511 MeV y energía total E = 10 MeV . Use Ec.de cuadrados

35. Problema : Encontrar mc 2 y u (dados p, E) Encontrar la masa en reposo y rapidez u de una particula con momentum pc = 300 MeV y energía total E = 3500 MeV . Use Ec. de cuadrados

36. Problema : Encontrar E, pc y u (dados K, mc 2 ) Un proton de 2-GeV choca con otro proton de 2-GeV en una colision frontal. Encontrar la energia total E, momentum pc , y velocidad u de cada proton. Use Ecs. Simple y cuadrada

37. Problema : Encontrar mc 2 y K EG , Baski Una particula S decae en un neutron (pc = 4702 MeV) y un pion (pc = 169 MeV). Encontrar la energia de la masa en reposo total y la energia cinetica de la particula S.

40. Masa en Reposo : Problema Ejemplo Por lo tanto, el Sol pierde 4.3x10 9 kg de masa cada segundo! A esta razón, el Sol debería agotarse de combustible después de ~ 10 11 años. Calcule la razón en el cual el Sol pierde masa, dado que el radio promedio R de la orbita terrestre es = 1.50×10 8 km, y la intensidad de radiación solar en la Tierra (constante solar) is 1.36×10 3 W/m 2 Asumimos que el Sol radia uniformemente sobre una esfera de radio R, la Potencia Total P radiada por el Sol es dado por: /s per second

41. Masa en Reposo : Problema Domiciliario Dos particulas identicas con masa en reposo de 12 kg se aproximan cada uno al otro con igual pero velocidades opuestas u 1 = –u 2 = 0.6c . Encontrar la masa total en reposo de este sistema.

42. Masa en reposo : Problema Domiciliario Un electron esta moviendose hacia la izquierda con velocidad 0.995c y un positron esta moviendose hacia la derecha con velocidad 0.9798c . Dibujar un diagrama y encontrar la Energía de la masa total en reposo de este sistema.

43. Transformación de Lorentz de E,p Derivación de:

44. Energia & Momentum 3-D Case 4-D Momentum Energia y Momentum estan separados en 3-D y Tienen separadas leyes de conservación. En 4-D son parte del mismo vector y las rotaciones preservan la longitud (norm).

46. Transformaciones de Lorentz : Problema Domiciliario Dos electrones cada uno con energia total E = 30 GeV se aproximan uno al otro con igual pero opuesta velocidad. Encontrar el momentum p de cada electron antes de la colisión en el sistema lab . Tambien, encontra r la energia E’ y momentum p’ del el e ctron de la izquierda en el sistema de referencia del electron de la derecha . Note : Porque u~c, use la aproxima c ion E ~ pc.