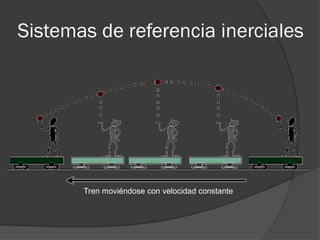
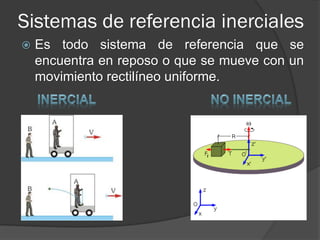
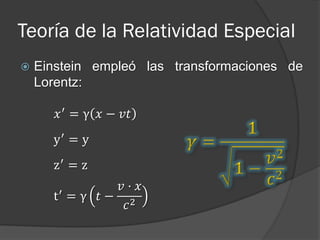
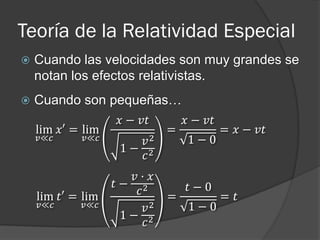
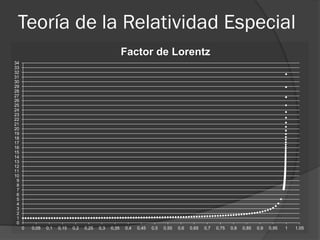
Las leyes de Newton y Maxwell explicaban los fenómenos hasta el siglo XX, pero no sistemas que se mueven a velocidades cercanas a la luz o sistemas atómicos. La mecánica cuántica y la teoría de la relatividad especial de Einstein resolvieron estas limitaciones al establecer que la velocidad de la luz es la misma para todos los observadores y que el tiempo y la longitud se ven afectados a velocidades altas.

1. TEMA 10

2. Limitaciones de la mecánica clásica

3. Limitaciones de la mecánica clásica
Hasta el s.XX las leyes de Newton y de
Maxwell pueden explicar cualquier fenómeno.
 Sistemas que se desplazan a velocidades
próximas a las de la luz.
 Sistemas atómicos.

4. Limitaciones de la mecánica clásica
Aceleración de electrones a grandes
velocidades:
 No cumplen el principio de conservación de
la energía mecánica.
 No eran capaces de sobrepasar la velocidad
de la luz.

5. Sistemas de referencia inerciales
Tren moviéndose con velocidad constante

6. Sistemas de referencia inerciales
 Es todo sistema de referencia que se
encuentra en reposo o que se mueve con un
movimiento rectilíneo uniforme.

7. Transformaciones de Galileo
Observador en O:
𝑥 𝑣𝑥 𝑎𝑥
𝑦 𝑣𝑦 𝑎𝑦
𝑧 𝑣𝑧 𝑎𝑧
𝑡
𝑂𝑏𝑠𝑒𝑟𝑣𝑎𝑑𝑜𝑟 𝑒𝑛 𝑂′ :
𝑥 ′ = 𝑥 − 𝑥0 𝑣 ′ 𝑥 = 𝑣 𝑥 − 𝑣0 𝑎′ 𝑥 = 𝑎 𝑥
𝑦′ = 𝑦 𝑣′ 𝑦 = 𝑣 𝑦 𝑎′ 𝑦 = 𝑎 𝑦
𝑧′ = 𝑧 𝑣′ 𝑧 = 𝑣 𝑧 𝑎′ 𝑧 = 𝑎 𝑧
𝑡′ = 𝑡

8. Transformaciones de Galileo
 La aceleración observada es la misma para
todos los observadores.
 Galileo concluyó que si las aceleraciones son
idénticas en cualquier sistema de referencia
inercial, las causas que las provocan han de
ser las mismas.
 Principio de relatividad de Galileo: las leyes
de la física son invariantes respecto a dos
observadores que se mueven con
movimiento uniforme, uno respecto al otro.

9. Teoría de la Relatividad Especial

10. Teoría de la Relatividad Especial
 En el siglo XIX se pensaba que la luz se
desplazaba como una onda mecánica.
 El medio por el que se desplazaba se
conocía como éter.
 Michelson y Morley intentaron detectar el
éter a través de su interferómetro pero se
llevaron una sorpresa.

11. Teoría de la Relatividad Especial
 Las leyes de Maxwell no eran invariantes
para dos sistemas inerciales.
 Lorentz descubrió una transformación de
velocidades para el electromagnetismo.
 Mostró que estas transformaciones dejaban
invariantes las ecuaciones de Maxwell.

12. Teoría de la Relatividad Especial
1. Las leyes de la Física tienen la misma
expresión en todos los sistemas de
referencia inerciales.
2. La velocidad de la luz es la misma en todos
los sistemas de referencia inerciales.
 Estos postulados de Einstein no son
compatibles con las transformaciones de
Galileo debido a que 𝑐 = 𝑐 𝑡𝑒 .

13. Teoría de la Relatividad Especial
 Einstein empleó las transformaciones de
Lorentz:
𝑥 ′ = γ 𝑥 − 𝑣𝑡
y′ = y
z′ = z
′
𝑣· 𝑥
t =γ 𝑡− 2
𝑐

14. Teoría de la Relatividad Especial
 Cuando las velocidades son muy grandes se
notan los efectos relativistas.
 Cuando son pequeñas…
𝑥 − 𝑣𝑡 𝑥 − 𝑣𝑡
lim 𝑥′ = lim = = 𝑥 − 𝑣𝑡
𝑣≪𝑐 𝑣≪𝑐 𝑣2 1−0
1− 2
𝑐
𝑣· 𝑥
𝑡− 2 𝑡−0
lim 𝑡′ = lim 𝑐 = = 𝑡
𝑣≪𝑐 𝑣≪𝑐 𝑣2 1−0
1− 2
𝑐

15. Teoría de la Relatividad Especial
Factor de Lorentz
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 0,4 0,45 0,5 0,55 0,6 0,65 0,7 0,75 0,8 0,85 0,9 0,95 1 1,05

16. Teoría de la Relatividad Especial
 Si dos objetos se mueven con velocidad 𝑣1 y
𝑣2 , cercanas a la velocidad de la luz:
𝑣2 − 𝑣1
𝑣′2 = 𝑣1 · 𝑣2
1−
𝑐2
Donde 𝑣′2 es la velocidad del segundo objeto
visto por el primero.

17. Consecuencias de la Relatividad

18. Dilatación del tiempo
 El intervalo de tiempo es mayor si lo mide el
observador en reposo.
 El tiempo se dilata si se mide desde un
sistema de referencia que viaja a la misma
velocidad.

19. La paradoja de los dos gemelos
 Dos gemelos de 25 años se separan porque
uno de ellos viaja a un planeta de otro
Sistema Solar situado a 20 años luz de la
Tierra.
 La nave lleva una velocidad constante de
0′ 8 𝑐.
 ¿Qué edad tienen cuando se reencuentran?

20.  Tiempo que mide el que se queda en la
Tierra:
𝑑 2 · 20𝑐
∆𝑡 = = ′ = 50 𝑎ñ𝑜𝑠
𝑣 0 8𝑐
 Edad actual: 25 𝑎ñ𝑜𝑠 + 50 𝑎ñ𝑜𝑠 = 𝟕𝟓 𝒂ñ𝒐𝒔

21.  Tiempo que mide el reloj del viajero:
∆𝑡 0′ 8𝑐 2
∆𝑡 ′ = = 50 𝑎ñ𝑜𝑠 · 1 −
𝛾 𝑐2
∆𝑡 ′ = 50 𝑎ñ𝑜𝑠 · 0′ 6 = 30 𝑎ñ𝑜𝑠
 Edad actual: 25 𝑎ñ𝑜𝑠 + 30𝑎ñ𝑜𝑠 = 55 𝑎ñ𝑜𝑠

22. Contracción de la longitud
 Las dimensiones de los objetos se contraen
en la dirección del movimiento:
𝑙 = 𝑥 𝐵 − 𝑥𝐴
𝑙 ′ = 𝑥′ 𝐵 − 𝑥′ 𝐴
 Aplicamos las transformaciones de Lorentz
𝑥′ 𝐴 = γ 𝑥 𝐴 − 𝑣𝑡 𝑦 𝑥′ 𝐵 = γ 𝑥 𝐵 − 𝑣𝑡

23. Contracción de la longitud
 Restamos:
𝑙 ′ = 𝑥′ 𝐵 − 𝑥 ′ 𝐴 = γ 𝑥 𝐵 − 𝑣𝑡 − γ 𝑥 𝐴 − 𝑣𝑡
𝑙 ′ = 𝛾 𝑥 𝐵 − 𝑣𝑡 − 𝑥 𝐴 + 𝑣𝑡
𝑙 ′ = 𝑥′ 𝐵 − 𝑥 ′ 𝐴 = 𝛾 𝑥 𝐵 − 𝑥 𝐴

24.  La longitud de una nave espacial es de 30 m,
medida desde la Tierra.
 Cuando fue lanzada medía 50 m.
 Calcula la velocidad de la nave.

25.  Aplicamos la expresión de contracción relativista
de la longitud:
′
𝑙′
𝑙 = 𝛾· 𝑙 → 𝛾=
𝑙
𝑣2 𝑙′ 𝑙′2 30 𝑚 2
1− 2 = → 𝑣 = 𝑐 1− 2 = 𝑐 1− 2
𝑐 𝑙 𝑙 50 𝑚
𝑣 = 0′ 8𝑐

26. Masa relativista
 A medida que aumenta la velocidad se
produce un incremento del valor de la masa
respecto de la situación de esta en reposo:

27. Equivalencia Masa – Energía
 La energía necesaria para que un cuerpo
pase del reposo a tener una velocidad v es:
 Donde 𝐸0 = 𝑚0 𝑐 2 es la energía de la masa
en reposo.

28. Equivalencia Masa – Energía
 Para valores de la velocidad mucho menores
que c:
1
𝐸 𝑐 = 𝑚0 𝑣 2
2

29.  La masa en reposo de un neutrón es
𝑚 𝑛 = 1′ 674927 · 10−27 𝑘𝑔. Calcula:
a) Su energía en reposo.
b) Su energía cinética cuando se mueve a una
velocidad 𝑣 = 0′ 5 𝑐.

30. a) La energía en reposo:
𝐸0 = 𝑚0 𝑐 2
𝐸0 = 1′ 674927 · 10−27 𝑘𝑔 · 3 · 108 𝑚/𝑠 2
𝐸0 = 1′ 5074 · 10−10 𝐽 ≈ 9′ 4 · 108 𝑒𝑉

31. b) Energía cinética:
𝑚0 2
1
𝐸𝑐 = − 𝑚0 𝑐 = −1 𝑚0 𝑐 2
𝑣2 𝑣2
1− 2 1− 2
𝑐 𝑐
1
𝐸𝑐 = −1 𝐸0 = 0′ 1547 · 𝐸0
0′ 5𝑐 2
1−
𝑐2
𝐸 𝑐 = 2′ 33 · 10−11 𝐽 ≈ 1′ 5 · 108 𝑒𝑉