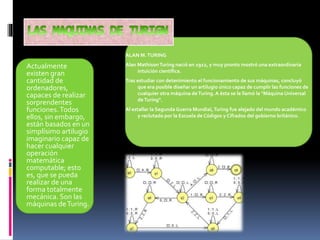
Este documento presenta una introducción a las máquinas de Turing y los modelos abstractos de máquinas (MAM). Explica que un MAM es un modelo matemático que puede representar el funcionamiento de sistemas reales como computadoras. Luego describe que Alan Turing propuso la máquina universal de Turing, capaz de simular cualquier otra máquina de Turing. Finalmente, introduce los conceptos de isomorfismo entre máquinas y su relación con la equivalencia de lenguajes generados.

1. YOSEL EVIEZ 25147147

3. Esta revista va
dirigida a aquellas
personas que
busca expandir sus
cocimientos sobre
u poco de
ingeniería.
De la mejor manera,
la digitalización
permite llegar a
muchas mas
personas y de
manera mas
sencilla.
Con el objetivo
de la
recreación
metal y el
entretenimie
nto.
YOSEL EVIEZ 25147147

4. No, no te estamos hablando
de una constructora.
Quizá hayas visto alguna
vez en la calle algún
dispensador de refresco o
u cajero automático …
pues felicidades ya viste
M.E.F.
Es un Modelo abstracto de
una máquina con memoria
interna primitiva. Se
puede considerar a un
computador como una
máquina de este tipo.
Ahora pues la definición no
formal dice que:
Se trata de un modelo
matemático, representado
con recursos formales (que
se especificarán
posteriormente), y que
puede emplearse para
representar o simular el
funcionamiento de un
sistema real, que puede ser
electrónico o
computacional o de otro
tipo. Esto es muy útil, ya
que posteriormente al
diseño formal, se puede
implementar en forma
sencilla por medio de un
programa escrito en
cualquier lenguaje de
programación.

5. Instituto Superior de Formación
Técnica
YOSEL EVIEZ 25147147

6. Actualmente
existen gran
cantidad de
ordenadores,
capaces de realizar
sorprendentes
funciones.Todos
ellos, sin embargo,
están basados en un
simplísimo artilugio
imaginario capaz de
hacer cualquier
operación
matemática
computable; esto
es, que se pueda
realizar de una
forma totalmente
mecánica. Son las
máquinas deTuring.
ALAN M.TURING
Alan MathisonTuring nació en 1912, y muy pronto mostró una extraordinaria
intuición científica.
Tras estudiar con detenimiento el funcionamiento de sus máquinas, concluyó
que era posible diseñar un artilugio único capaz de cumplir las funciones de
cualquier otra máquina deTuring. A ésta se le llamó la "Máquina Universal
deTuring".
Al estallar la Segunda Guerra Mundial,Turing fue alejado del mundo académico
y reclutado por la Escuela de Códigos y Cifrados del gobierno británico.

7. ISOMORFISMO DE MAQUINAS
Se dice que A1 es isomorfo a A2,
es decir, A1»A2 si $ i :Q1®Q2, (i :
imagen). Por lo tanto :
i(p01) = p02 (la imagen del
estado inicial de A1 es el estado
inicial de A2.
Dados pÎF1, qÎF2 : i(p)ÎF2, y
i(q)ÎF1.(es decir, la imagen de los
estados finales de uno de los
máquinas, es un estado final del
otro máquina).
i(f1(p1,e)) = f2(i(p1),e) =
f2(i(p2),e).La imagen de la
transición es la transición de la
imagen. Por lo tanto A1 y A2
son iguales renombrando
estados.
Entonces si dos máquinas son
isomorfos van a ser
equivalentes, es decir, los
lenguajes que van a generar
ambos máquinas van a ser el
mismo : L(A1) = L(A2). Con esto
comprobamos que la isomorfía
implica la equivalencia.
Teorema : Si dos
máquinas son
equivalentes,
entonces sus
máquinas
mínimos son
isomorfos, es
decir :A1EA2 Þ
Â1»Â2 (siendo  i
º máquina
mínimo deAi).
Máquina para venta de refrescos.
Ya que el estado actual (cantidad de dinero que se ha depositado
en ella) junto con la entrada actual (la moneda que se está depositando
en cada momento) determinan la salida que el aparato entrega (nada,
cambio, refresco, refresco y cambio). La misma moneda produce
diferentes salidas.
Cajero automático.
Ya que la entrada (tarjeta, NIP, botón) debe combinarse
con una correcta serie de transiciones por los estados (espera usuario,
espera NIP, espera requisición de servicio, etc.) para que se pueda
obtener la salida deseada (billetes, impresiones de estado de cuenta,
etc.). La entrada "solicito $100" en el estado "espera NIP" no produce el
efectivo requerido.
Circuitos secuenciales digitales.
Ya que en los circuitos de este tipo, es necesario conocer el
potencial o voltaje que guardan ciertos puntos dentro de los mismos (es
decir, los estados) para que en combinación con los valores de los bits de
entrada, se conozcan los de salida. En un simple flip-flop, se requiere de
conocer el estado del mismo para saber qué salida presenta.

8. ¿Quieres publicidad?
Contáctanos
+58-412-000-0010
YOSEL EVIEZ 25147147