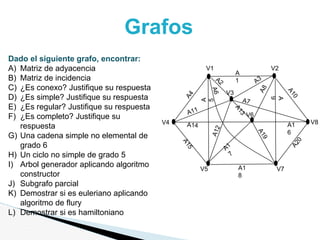
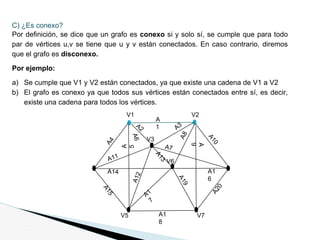
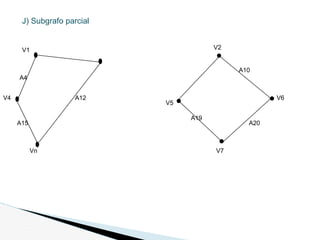
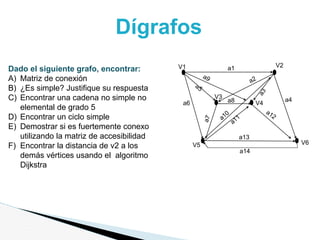
Este documento presenta un problema sobre grafos y dígrafos. Para un grafo no dirigido se pide encontrar la matriz de adyacencia, verificar si es conexo, simple, regular, completo, etc. También se pide encontrar cadenas, ciclos y demostrar si es euleriano o hamiltoniano. Para un dígrafo se pide encontrar la matriz de conexión, verificar si es simple, encontrar cadenas y ciclos, demostrar si es fuertemente conexo y encontrar distancias usando Dijkstra. El documento contiene las definiciones y pasos para resolver cada

1. UNIVERSIDAD FERMÍN TORO
VICERRECTORADO ACADÉMICO
FACULTAD DE INGENIERÍA
YOSEL EVIZ
SAIA
Estructuras
Discretas II

2. Dado el siguiente grafo, encontrar:
A) Matriz de adyacencia
B) Matriz de incidencia
C) ¿Es conexo? Justifique su respuesta
D) ¿Es simple? Justifique su respuesta
E) ¿Es regular? Justifique su respuesta
F) ¿Es completo? Justifique su
respuesta
G) Una cadena simple no elemental de
grado 6
H) Un ciclo no simple de grado 5
I) Arbol generador aplicando algoritmo
constructor
J) Subgrafo parcial
K) Demostrar si es euleriano aplicando
algoritmo de flury
L) Demostrar si es hamiltoniano
Grafos
V1 V2
V8V4
V3
V6
V5 V7
A
1
A
5
A
9
A1
6
A1
8

3. A) Matriz de adyacencia: para
desarrollar esta matriz, se debe
encontrar la multiplicidad entre los
vértices. La multiplicidad es el
número de aristas que existen entre
cada par de vértices.
Ma(G)=
B) Matriz de incidencia: es el número
de veces que la arista incide en el
vértice.
V1 V2 V3 V4 V5 V6 V7 V8
V1
V2
V3
V4
V5
V6
V7
V8
Mi(G)=
V1 V2 V3 V4 V5 V6 V7 V8
A1
A2
A3
A4
A5
A6
A7
A8
A9
A10
A11
A12
A13
A14
A15
A16
A17
A18
A19
A20

4. C) ¿Es conexo?
Por definición, se dice que un grafo es conexo si y solo sí, se cumple que para todo
par de vértices u,v se tiene que u y v están conectados. En caso contrario, diremos
que el grafo es disconexo.
Por ejemplo:
a) Se cumple que V1 y V2 están conectados, ya que existe una cadena de V1 a V2
b) El grafo es conexo ya que todos sus vértices están conectados entre sí, es decir,
existe una cadena para todos los vértices.
V1 V2
V3
V6
V5 V7
A
1A
5
A
9
A1
6
A1
8

5. D) ¿Es simple?
Según la definición, un grafo se denomina simple si y solo sí, no tiene lazos y entre cada par
de vértices distintos no hay más de una arista. Si se observa el grafo planteado, se puede
notar que no existen lazos y tampoco hay más de una arista entre cada par de vértices, por lo
tanto es un grafo simple. Por ejemplo, de V1 a V2 hay una arista, y de V1 a V4 también hay
solo una arista.
E) ¿Es regular?
Un grafo simple en el que todos los vértices tienen grado r es llamado grafo regular de grado
r, en el punto anterior se demostró que el grafo es simple, por ende, el grafo es regular.
F) ¿Es completo?
Un grafo se denomina completo si es un grafo simple y solo existe exactamente una arista
entre cada par de vértices. Observando el grafo dado, se puede ver que entre cada par de
vértices solo hay una arista. Por ejemplo, de V3 a V6 esta A13, y de V3 a V2 solo existe
A3

6. G) Una cadena simple no elemental de grado 6
Una cadena simple es la que no repite aristas, y una cadena elemental es la que
no repite vértices, por lo tanto una cadena NO elemental es la que repite
vértices. A continuación, se presenta dicha cadena:
V2
V3
V6
V5 V7
A
1
A
5
A
9
A1
6
A1
8
V1
V4 V8 C1= [V1, A1, V2, A3, V3, A2, V1,
A5, V5, A15, V4]

7. H) Un ciclo no simple de grado 5
Un ciclo simple es aquel en donde no se repiten aristas, solo la del inicio y final, por lo
tanto, en un ciclo no simple si se pueden repetir las aristas sin importar cuantas veces
pase por el vértice.
V2
V3
V6
V5 V7
A
1
A
5
A
9
A1
6
A1
8
V1
V4 V8
C1= [V5, A17, V6, A19, V7, A18,
V5, A15, V4
I) Demostrar si es hamiltoniano
Un grafo es hamiltoniano si la cadena
contiene todos los vértices sin repetirse.
Este grafo es hamiltoniano ya que:
C1= [V1, A1, V2, A3, V3, A11, V4, A15, V5, A17,
V6, A19, V7, A20, V8]
C2= [V2, A1, V1, A2, V3, A11, V4, A15, V5, A17,
V6, A19, V7, A20, V8]
C3= [V3, A3, V2, A1, V1, A4, V4, A15, V5, A17,
V6, A19, V7, A20, V8]
C4= [V4, A15, V5, A17, V6, A19, V7, A20, V8,
A10, V2, A3, V3, A2, V1]
C5=[V5, A17, V6, A19, V7, A20, V8, A10, V2, A3,
V3, A2, V1, A4, V4]
C6=[V6, A19, V7, A20, V8, A10, V2, A3, V3, A2, V1, A4, V4
A15, V5]
C7=[V7, A20, V8, A10, V2, A3, V3, A2, V1, A4, V4, A15, V5
A17, V6]
C8=[V8, A10, V2, A3, V3, A2, V1, A4, V4, A15, V5, A17, V6
A19, V7]

8. J) Subgrafo parcial
V1
V4
Vn
A12
A4
A15
V2
V6
V7
V5
A10
A20
A19

9. k) Demostrar que es euleriano con el algoritmo de fleury
V1 V2
V8V4
V3
V6
V5 V7
A
1
A
5
A
9
A1
6
A1
8
Comenzamos con el grafo plasmado,
aplicando el algoritmo de fleury donde
nos indica eliminar las aristas que no
sean puentes; a menos que no haya
otra opcion damos con el siguiente
resultado.
V1 V2
V8V4
V3
V6
V5 V7
A16
A18
En vista de que solo nos quedan
aristas puente las eliminamos
todas obteniendo como resultado
el euleriano:
Grafo euleriano:
v1v2,v1v8,v1v7,v2v8,v4v5,v2v5,v7v3,
v6v8,v3v5,v1v3

10. Dígrafos
Dado el siguiente grafo, encontrar:
A) Matriz de conexión
B) ¿Es simple? Justifique su respuesta
C) Encontrar una cadena no simple no
elemental de grado 5
D) Encontrar un ciclo simple
E) Demostrar si es fuertemente conexo
utilizando la matriz de accesibilidad
F) Encontrar la distancia de v2 a los
demás vértices usando el algoritmo
Dijkstra
V1 V2
V5 V6
V3
V4
a1
a4
a6 a8
a13
a14

11. A) Matriz de conexión: la matriz
de conexión se realiza con la
multiplicidad de todos los pares
de vértices, de la siguiente
forma:
V1 V2 V3 V4 V5 V6
V1
V2
V3
V4
V5
V6
B) ¿Es simple? Por definición, un
dígrafo es simple si no contiene lazos
ni arcos paralelos. Los arcos
paralelos se identifican cuando el
origen de a1=a2 y final de a1= a2. Es
decir, el inicio y final de dos aristas
coinciden.
Por ejemplo:
a) El ejemplo del dígrafo presentado
es simple, ya que no contiene lazos
ni arcos paralelos, solo una pareja de
arcos opuestos, que son a13 y a14

12. C) Encontrar una cadena no simple
no elemental de grado 5
Una cadena no simple es cualquier
trayectoria que repita arcos y una
cadena no elemental es cualquier
trayectoria que repita vértices. A
continuación, se presenta la
siguiente cadena:
V2
V5
V3
V4
a1
a4
a6 a8
a13
a14
V1
V6
C1=[V5, A10, V2, A4, V6, A14,
V5, A13, V6]

13. C) Encontrar un ciclo simple
Un ciclo es simple cuando una
trayectoria no repite arcos. Por
ejemplo:
V1 V2
V5 V6
V3
V4
a1
a4
a6 a8
a13
a14
C1=[V1, A1, V2, A3, V4, A9, V1]

14. D) Demostrar si es fuertemente
conexo utilizando la matriz de
accesibilidad
McD=
v1 v2 v3 v4 v5 v6
v1 0 1 1 0 1 0
v2 0 0 1 1 0 1
v3 0 0 0 1 1 0
v4 1 0 0 0 0 1
v5 0 1 0 1 0 1
v6 0 0 0 0 1 0
v1 v2 v3 v4 v5 v6
v1 0 1 1 1 1 1
v2 1 0 0 1 1 1
v3 1 1 0 1 0 1
v4 0 1 1 0 1 0
v5 1 0 1 1 1 1
v6 0 1 0 1 0 1
M2=

15. v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 0 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 0 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
M3=
M5=
M4=
M6=

16. Mi=
v1 v2 v3 v4 v5 v6
v1 31 40 33 65 62 79
v2 22 33 24 47 47 58
v3 20 26 22 39 43 49
v4 16 29 21 42 38 48
v5 23 34 25 49 53 60
v6 11 14 12 23 23 30
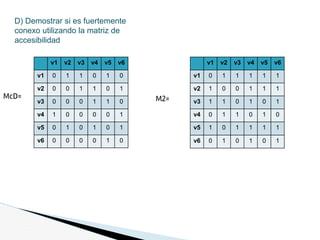
Para concluir : Acc(D)=bin= [I7 + M+M2+M3+M4+M5+M6]
v1 v2 v3 v4 v5 v6
v1 1 0 0 0 0 0
v2 0 1 0 0 0 0
v3 0 0 1 0 0 0
v4 0 0 0 1 0 0
v5 0 0 0 0 1 0
v6 0 0 0 0 0 1
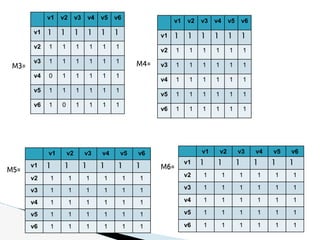
v1 v2 v3 v4 v5 v6
v1 1 1 1 1 1 1
v2 1 1 1 1 1 1
v3 1 1 1 1 1 1
v4 1 1 1 1 1 1
v5 1 1 1 1 1 1
v6 1 1 1 1 1 1
Como la matriz de
accesibilidad no
tiene componentes
nulos se puede
afirmar que el
dígrafo es
fuertemente
conexo
=

17. V1 V2
V5 V6
V3
F) Encontrar la distancia de v2 a los demás vértices
usando el algoritmo Dijkstra
3
3
En esta diapositiva se puede ver cómo quedó el cálculo de la distancia más corta
entre V2 y V5
(6,1)
V4
(8,1)
(3,1)
(3,1)
(4,1)
De V2 a V1: 8
De V2 a V3: 3
De V2 a V4: 4
De V2 a V5: 6
De V2 a V6: 3