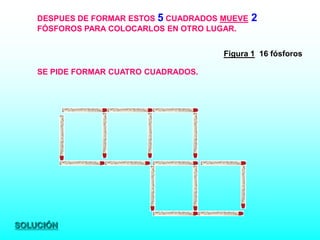
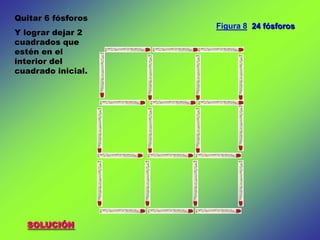
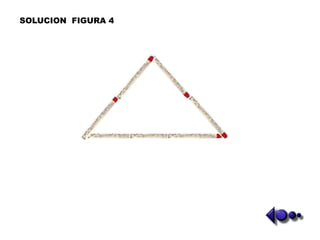
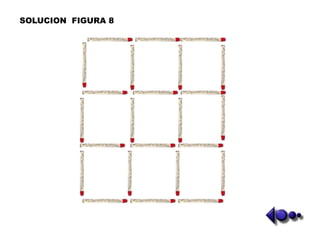
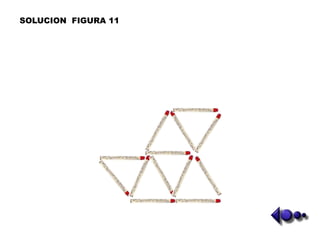
Este documento presenta un taller de matemáticas que usa fósforos para resolver problemas lógicos y de transformación de figuras. Los estudiantes deben mover un número limitado de fósforos para cambiar las figuras de acuerdo a las instrucciones del profesor. El taller contiene 14 problemas con figuras de entre 6 y 24 fósforos cada una.

1. TALLER DE MATEMÁTICAS
• TRABAJANDO EL INGENIO DE LOS
ALUMNOS DE SAN RAFAEL
JUGANDO CON PALITOS DE FÒSFOROS
Prof. MATEMÁTICAS
Ernesto Palma C.
dixi_7@hotmail.com

2. DESARROLLO DEL PENSAMIENTO LÓGICO
• Sigue atentamente las instrucciones y
ordenadamente cumple con lo solicitado.
• Puedes ayudarte con una hoja y un lápiz.
• Si lo haces en orden, no botaras tus
fósforos.
Resolver cada uno de los siguientes problemas, transformando
las figuras hechas con fósforos de acuerdo a lo solicitado
por tu profesor.

3. DESPUES DE FORMAR ESTOS 5 CUADRADOS MUEVE 2
FÓSFOROS PARA COLOCARLOS EN OTRO LUGAR.
Figura 1 16 fósforos
SE PIDE FORMAR CUATRO CUADRADOS.
SOLUCIÓN

4. Figura 2 12 fósforos
Mueve sólo 4 fósforos y los 3
rombos se convertirán en cuatro
rombos
SOLUCIÓN

5. Figura 3 18 fósforos
Con mover 6
fósforos, construye
otra estrella de seis
puntas con la
misma cantidad de
fósforos
SOLUCIÓN

6. Figura 4 7 fósforos
A partir de este triángulo formado por 7
fósforos, construir 3 triángulos, moviendo sólo 3
fósforos.
SOLUCIÓN

7. Figura 5 18 fósforos
En esta figura se pueden
Contar 9 triángulos
Iguales:
Se puede hacer desaparecer 5 triángulos, moviendo sólo 4
fósforos...
SOLUCIÓN

8. FOSFORITOS QUE SE VAN
Figura 6 12 fósforos
Usando la figura
siguiente, retirar 2
fósforos para que
queden solamente
dos cuadrados.
SOLUCIÓN

9. Retirando 4 fósforos Figura 7 16 fósforos
Transformar esta figura
En 4 triángulos.
SOLUCIÓN

10. Quitar 6 fósforos
Figura 8 24 fósforos
Y lograr dejar 2
cuadrados que
estén en el
interior del
cuadrado inicial.
SOLUCIÓN

11. Retirando Figura 9 24 fósforos
4 fósforos
Transformar
Esta figura
En cinco
Cuadrados.
SOLUCIÓN

12. Figura 10 24 fósforos
Quitar 8
fósforos y dejar
Solamente 2
cuadrados.
SOLUCIÓN

13. Figura 11 13 fósforos
Retirando 3 fósforos
transformar esta figura
En tres triángulos.
SOLUCIÓN

14. Figura 12 8 fósforos
El pez de esta
figura está
hecho con ocho
fósforos.
Moviendo solo
4 fósforos, se
puede hacer
que tome el
camino
contrario.
SOLUCIÓN

15. Formar dos paralelogramos de
Figura 13 6 fósforos
igual superficie moviendo sólo
dos fósforos y agregando uno
más.
SOLUCIÓN

16. En el interior del rectángulo Figura 14 10 fósforos
formado por diez fósforos hay
muchos gusanitos en fila...
¿Cómo hacer para tener el doble de
gusanitos en el interior de la figura
agregando sólo dos fósforos?
SOLUCIÓN

17. SOLUCION FIGURA 1

18. SOLUCION FIGURA 2

19. SOLUCION FIGURA 3

20. SOLUCION FIGURA 4

21. SOLUCION FIGURA 5

22. SOLUCION FIGURA 6

23. SOLUCION FIGURA 7

24. SOLUCION FIGURA 8

25. SOLUCION FIGURA 9

26. SOLUCION FIGURA 10

27. SOLUCION FIGURA 11

28. SOLUCION FIGURA 12

29. SOLUCION FIGURA 13

30. SOLUCION FIGURA 14

31. Bibliografía.
Matemática Recreativa en el aula
Autoras: Alicia Cofre .
Lucila tapia A.
Editorial U. Católica. de Chile y Fundación Educ. Arauco
Prof. MATEMÁTICAS Esc. San Rafael Talca Chile
Ernesto Palma C.
dixi_7@hotmail.com