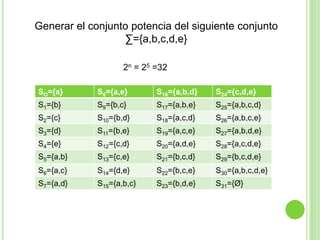
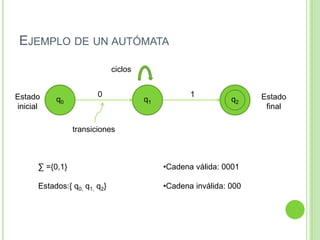
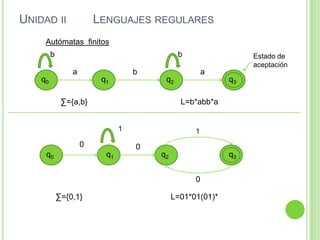
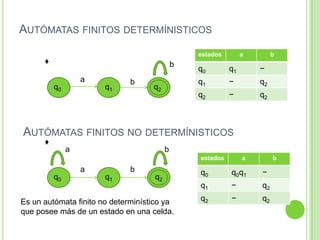
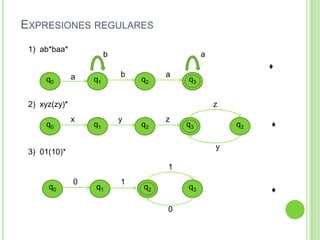
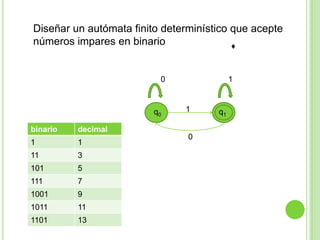
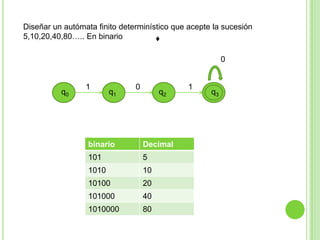
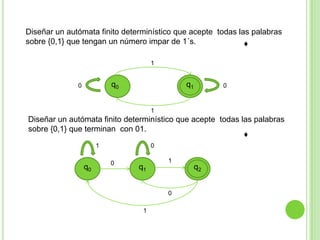
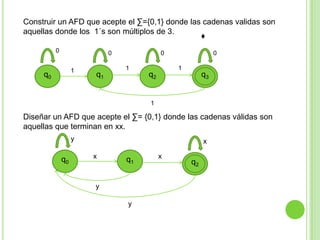
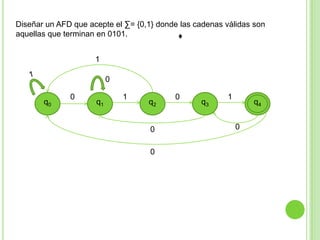
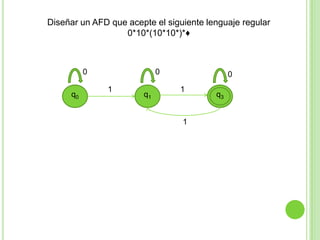
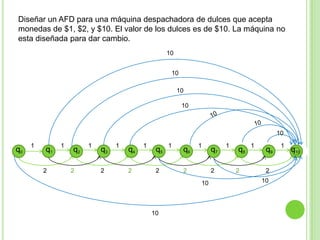
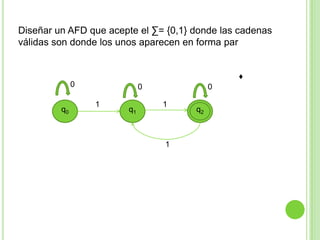
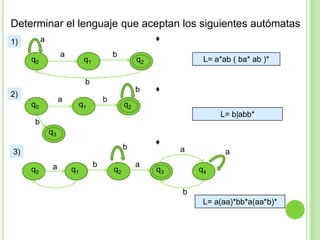
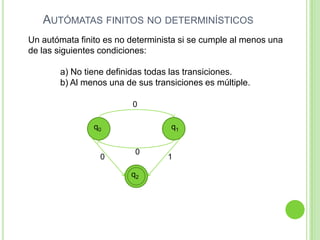
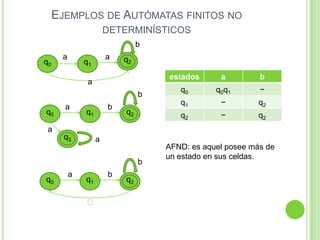
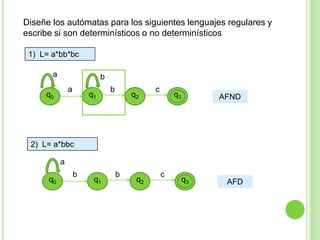
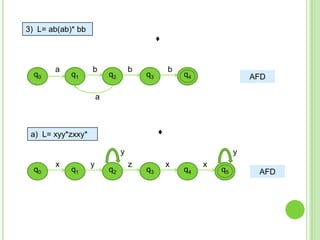
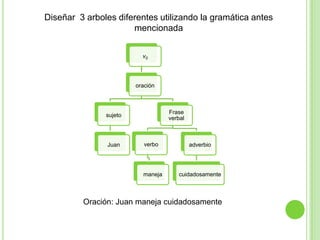
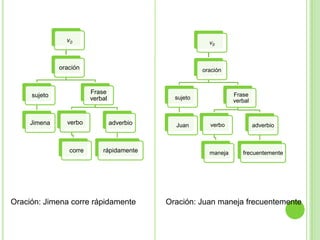
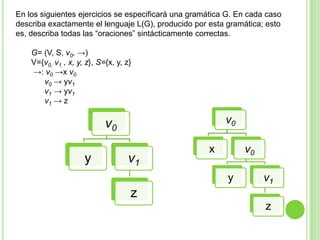
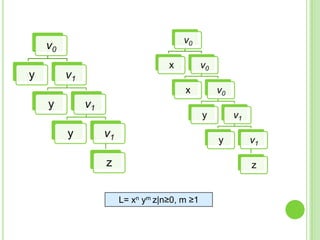
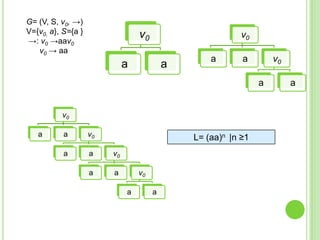
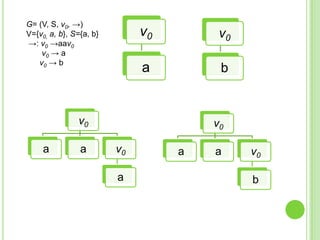
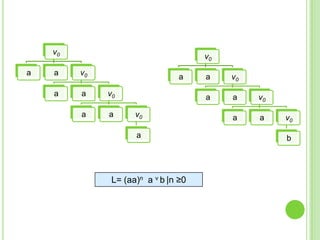
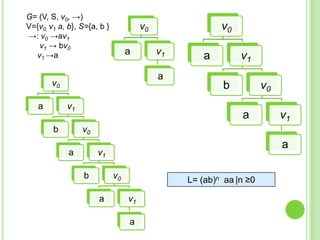
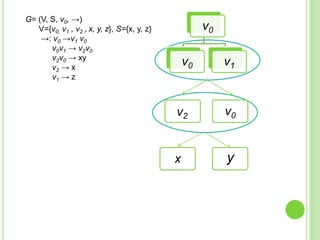
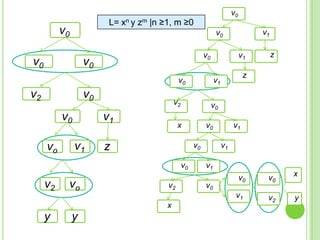
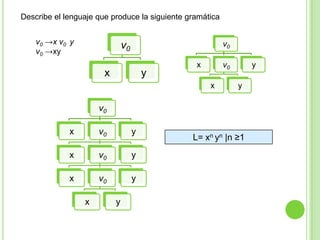
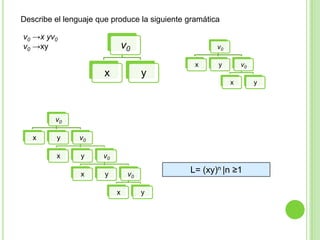
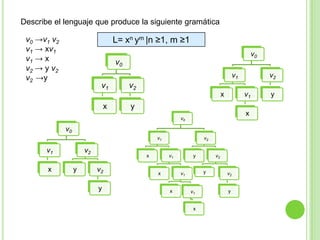
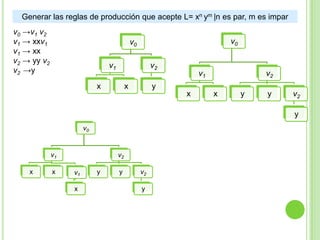
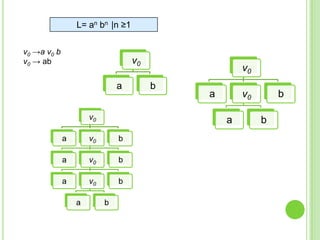
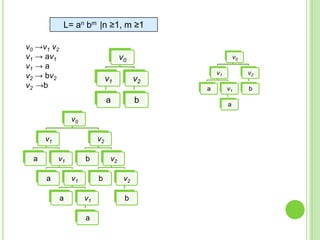
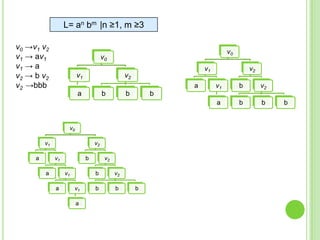
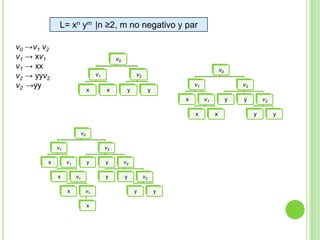
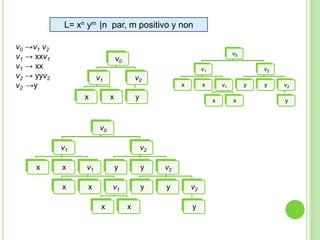
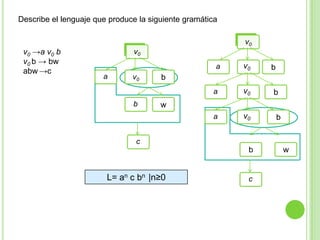
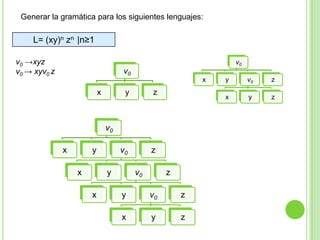
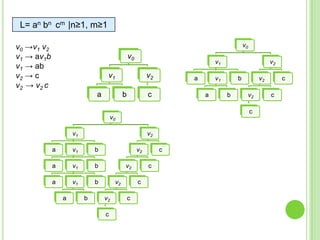
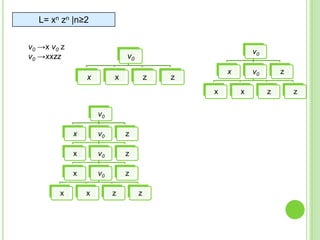
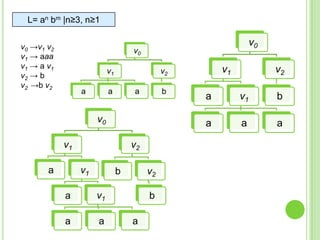
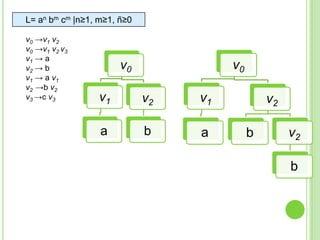
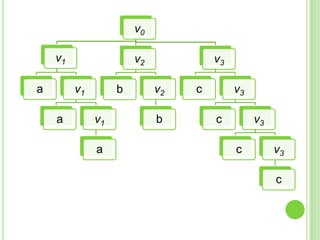
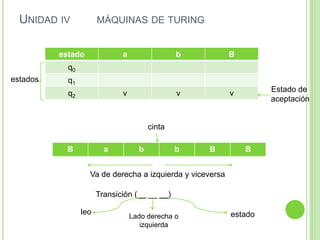
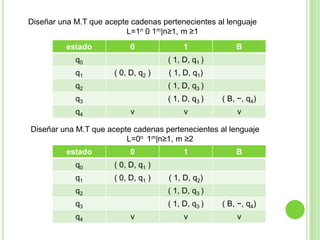
Este documento presenta apuntes sobre la teoría de la computación. Introduce conceptos básicos como conjuntos, subconjuntos, conjunto potencia y cadenas. Explica autómatas finitos determinísticos y no determinísticos y cómo modelar lenguajes regulares con ellos. Finalmente, introduce gramáticas formales y lenguajes libres de contexto, mostrando ejemplos de gramáticas y los lenguajes que generan.

1. MATERIA: TEORÍA DE LA COMPUTACIÓN
CATEDRÁTICO:
OLIVIA GUADALUPE LÓPEZ RUÍZ
Apuntes de la materia

2. UNIDAD
I

3. CONJUNTOS
Definición:
Un conjunto es un grupo o colección de objetos, a los que se le
conoce como elementos o miembros del mismo.
Notación:
Una forma de describir un conjunto con un numero finito de
elementos, es hacer una lista de elementos del conjunto y encerrarla
entre llaves. Ejemplo , el conjunto de todos lo enteros positivos
menores que 4.
A={1, 2 ,3 }
En cambio para representar un conjunto infinito utilizando la se
requiere hacer uso de la notación P(x), para denotar una oración o
enunciado P relativo al objeto variable x. El objeto definido por P(x),
escrito en la forma {x|P(x)} es simplemente la colección de todos los
objetos x para los cuales P es sensible y cierto. Ejemplo:
A={x| x es un entero positivo}

4. CONJUNTO POTENCIA
Definición:
El conjunto potencia es aquel que contiene todos los subconjuntos de
un conjunto original.
Para obtenerlo se utiliza la formula 2n donde n indica el número de
elementos del conjunto.
Ejemplos:
A={a,b,c}
2n = 23 =8
SO={a}
S4={a,c}
S1={b}
S5={b,c}
S2={c}
S6={a,b,c}
S3={a,b}
S7={Ø}
subconjuntos

5. Determinar todos los subconjuntos que se generan del
conjunto
A={0,1,2,3}
2n = 24 =16
SO={0}
S8={1,3}
S1={1}
S9={2,3}
S2={2}
S10={0,1,2}
S3={3}
S11={0,1,3}
S4={0,1}
S12={0,2,3}
S5={0,2}
S13={1,2,3}
S6={0,3}
S14={0,1,2,3}
S7={1,2}
S15={Ø}

6. Generar el conjunto potencia del siguiente conjunto
∑={a,b,c,d,e}
2n = 25 =32
SO={a}
S8={a,e}
S16={a,b,d}
S24={c,d,e}
S1={b}
S9={b,c}
S17={a,b,e}
S25={a,b,c,d}
S2={c}
S10={b,d}
S18={a,c,d}
S26={a,b,c,e}
S3={d}
S11={b,e}
S19={a,c,e}
S27={a,b,d,e}
S4={e}
S12={c,d}
S20={a,d,e}
S28={a,c,d,e}
S5={a,b}
S13={c,e}
S21={b,c,d}
S29={b,c,d,e}
S6={a,c}
S14={d,e}
S22={b,c,e}
S30={a,b,c,d,e}
S7={a,d}
S15={a,b,c}
S23={b,d,e}
S31={Ø}

7. CADENAS
Definición:
Una cadena (string) de caracteres es un conjunto de
caracteres(incluido el blanco, que se almacenan en
un área continua de memoria.
Longitud de cadena: Es el número de caracteres que
contiene la cadena.la cadena que no contiene ningún
carácter se denomina nula o vacía.
Concatenación de cadenas: Es la operación de reunir
varias cadenas de caracteres en una sola,
conservando el orden de sus caracteres.

8. Forma de representar los conceptos estudiados anteriormente:
Cadenas
Longitud
Reverso
x=lenguaje
y=agua
z=blanca
a=rojo
b=programacion
c=123
|lenguaje | =8
| agua | =4
| blanca | =6
| rojo | =4
| Programacion | =12
| 123 | =3
xr=ejaugnel
yr=auga
zr=acnalb
ar=ojor
br=noicamargorp
cr=321
Concatenación
y . z= aguablanca
x . b= lenguajeprogramacion

9. AUTÓMATAS

Autómata: Es una máquina formal que acepta un
alfabeto de entrada y produce una salida, es decir,
una máquina que valida cadenas y verifica si son
válidas o inválidas.
Los autómatas se clasifican en:
-Finitos determinísticos
-Finitos no determinísticos

10. EJEMPLO DE UN AUTÓMATA
ciclos
Estado
inicial
q0
0
q1
1
q2
transiciones
∑ ={0,1}
•Cadena válida: 0001
Estados:{ q0, q1, q2}
•Cadena inválida: 000
Estado
final

11. UNIDAD
II

12. UNIDAD II
LENGUAJES REGULARES
Autómatas finitos
b
b
a
Estado de
aceptación
b
q0
q1
a
q2
∑={a,b}
L=b*abb*a
1
0
q0
q3
1
0
q1
q2
q3
0
∑={0,1}
L=01*01(01)*

13. Diseñar un autómata finito que acepte el ∑={0,1} donde las cadenas validas
son aquellas que pertenecen a la sucesión 10, 20,,30 ,40,80 160… en
binario
0
1
q0
binario
0
q1
decimal
1010
10
10100
20
101000
40
1010000
80
10100000
160
101000000
320
1010000000
640
1
q2
0
q3
q4

14. AUTÓMATAS FINITOS DETERMÍNISTICOS
estados
♦
b
a
q0
q1
b
a
b
q1
−
q1
−
q2
q2
q2
q0
−
q2
AUTÓMATAS FINITOS NO DETERMÍNISTICOS
♦
a
b
estados
a
q0
b
q1
q2
Es un autómata finito no determinístico ya
que posee más de un estado en una celda.
a
b
q0
q0q1
−
q1
−
q2
q2
−
q2

15. EXPRESIONES REGULARES
1) ab*baa*
b
a
♦
q0
a
q1
b
q2
a
q3
2) xyz(zy)*
q0
z
x
q1
y
q2
z
q3
q2
♦
y
3) 01(10)*
1
q0
0
q1
1
q2
q3
0
♦

16. Diseñar un autómata finito determinístico que acepte
números impares en binario
♦
0
q0
binario
1
11
3
101
5
111
7
1001
9
1011
11
1101
13
1
decimal
1
1
0
q1

17. Diseñar un autómata finito determinístico que acepte la sucesión
5,10,20,40,80….. En binario
♦
0
q0
1
q1
0
q2
binario
Decimal
101
5
1010
10
10100
20
101000
40
1010000
80
1
q3

18. Diseñar un autómata finito determinístico que acepte todas las palabras
sobre {0,1} que tengan un número impar de 1´s.
♦
1
q0
0
q1
0
1
Diseñar un autómata finito determinístico que acepte todas las palabras
sobre {0,1} que terminan con 01.
♦
1
q0
0
0
q1
1
0
1
q2

19. Construir un AFD que acepte el ∑={0,1} donde las cadenas validas son
aquellas donde los 1´s son múltiplos de 3.
♦
0
0
1
q0
q1
0
1
0
1
q2
q3
1
Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas válidas son
aquellas que terminan en xx.
y
q0
x
x
q1
y
y
x
q2

20. Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas válidas son
aquellas que terminan en 0101.
♦
1
0
q0
0
q1
1
q2
0
0
0
q3
1
q4
0

21. Diseñar un AFD que acepte el siguiente lenguaje regular
0*10*(10*10*)*♦
0
q0
0
1
q1
0
1
1
q3

22. Diseñar un AFD para una máquina despachadora de dulces que acepta
monedas de $1, $2, y $10. El valor de los dulces es de $10. La máquina no
esta diseñada para dar cambio.
10
10
10
10
10
q0
1
q1
2
1
q2
2
1
q3
2
1
q4
2
1
q5
2
1
q6
1
2
2
10
10
q7
1
q8
2
1
q9
2
10
1
q10

23. Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas
válidas son donde los unos aparecen en forma par
♦
0
q0
0
1
q1
0
1
1
q2

24. Determinar el lenguaje que aceptan los siguientes autómatas
♦
a
1)
a
q0
b
q1
q2
b
b
2)
a
q0
b
q1
L= a*ab ( ba* ab )*
♦
q2
L= b|abb*
b
q3
♦
b
3)
q0
a
q1
b
q2
a
a
q3
a
q4
b
L= a(aa)*bb*a(aa*b)*

25. AUTÓMATAS FINITOS NO DETERMINÍSTICOS
Un autómata finito es no determinista si se cumple al menos una
de las siguientes condiciones:
a) No tiene definidas todas las transiciones.
b) Al menos una de sus transiciones es múltiple.
0
q0
0
q1
0
q2
1

26. EJEMPLOS DE AUTÓMATAS FINITOS NO
DETERMINÍSTICOS
b
q0
a
a
q1
q2
estados
q0
a
b
q1
q2
b
q0
q0q1
−
−
q2
q2
b
a
q1
a
−
q2
a
q3
a
b
q0
a
q1

b
q2
AFND: es aquel posee más de
un estado en sus celdas.

27. Diseñe los autómatas para los siguientes lenguajes regulares y
escribe si son determinísticos o no determinísticos
1) L= a*bb*bc
a
b
a
q0
q1
b
q2
c
q3
AFND
2) L= a*bbc
a
q0
b
q1
b
q2
c
q3
AFD

28. 3) L= ab(ab)* bb
♦
q0
a
q1
b
b
q2
b
q3
q4
AFD
a
♦
a) L= xyy*zxxy*
y
q0
x
q1
y
q2
y
z
q3
x
q4
x
q5
AFD

29. UNIDAD
III

30. UNIDAD III LENGUAJES LIBRES DE CONTEXTO
Gramática(G): una gramática se define por una 4-ada
(V, S, v0, →)
Gramática= (V, S, v0, →)
Donde:
V= Todas las cadenas permitidas
S= Subconjunto de todas las cadenas permitidas
v0= Inicio
→= Reglas de producción

31. Si G= (V, S, v0, →) es una gramática de estructura de frase, se llamará a S
conjunto de los símbolos terminales y a N= V − S conjunto de los
símbolos no terminales. Obsérvese que V= S U N
•símbolos terminales; aquellos que ya no pueden producir nada
•símbolos no terminales; siguen produciendo algo.
S={Juan, Jimena, maneja, corre, cuidadosamente, rápidamente,
frecuentemente}
N={oración, sujeto, frase verbal, verbo, adverbio}
V= S U N
V={Juan, Jimena, maneja, corre, cuidadosamente, rápidamente,
frecuentemente, oración, sujeto, frase verbal, verbo, adverbio}
v0= “oración”
→= todas las posibles combinaciones que la gramática permite

32. Oración → sujeto frase verbal
Sujeto → juan
Sujeto → jimena
Frase verbal → verbo adverbio
verbo → maneja
verbo →corre
adverbio → cuidadosamente
adverbio → rapidamente
adverbio → frecuentemente
El conjunto de todas las oraciones bien construidas que puede
producirse al usar una gramática G, se llama lenguaje de G y se
escribe L(G).

33. Diseñar 3 arboles diferentes utilizando la gramática antes
mencionada
v0
oración
Frase
verbal
sujeto
verbo
adverbio
maneja
Juan
cuidadosamente
Oración: Juan maneja cuidadosamente

34. v0
v0
oración
oración
Frase
verbal
sujeto
verbo
adverbio
corre
Jimena
Frase
verbal
sujeto
rápidamente
Oración: Jimena corre rápidamente
verbo
adverbio
maneja
Juan
frecuentemente
Oración: Juan maneja frecuentemente

35. En los siguientes ejercicios se especificará una gramática G. En cada caso
describa exactamente el lenguaje L(G), producido por esta gramática; esto
es, describa todas las “oraciones” sintácticamente correctas.
G= (V, S, v0, →)
V={v0, v1 , x, y, z}, S={x, y, z}
→: v0 →x v0
v0 → yv1
v1 → yv1
v1 → z
v0
v0
y
v1
x
v0
y
v1
z
z

36. v0
v0
y
x
v1
v0
x
y
v1
y
v0
y
v1
v1
y
z
v1
z
L= xn ym z|n≥0, m ≥1

37. G= (V, S, v0, →)
V={v0, a}, S={a }
→: v0 →aav0
v0 → aa
v0
v0
a
a
a
a
v0
a
v0
a
a
v0
a
a
v0
a
a
L= (aa)n |n ≥1
v0
a
a
a

38. G= (V, S, v0, →)
V={v0, a, b}, S={a, b}
→: v0 →aav0
v0 → a
v0 → b
v0
v0
a
b
v0
a
a
v0
v0
a
a
a
v0
b

39. v0
a
v0
a
v0
a
a
v0
a
a
a
a
L= (aa)n a v b |n ≥0
v0
a
v0
a
a
v0
a
a
v0
b

40. G= (V, S, v0, →)
V={v0, v1 a, b}, S={a, b }
→: v0 →av1
v1 → bv0
v1 →a
a
v1
a
v0
a
v0
v0
v1
b
a
v1
b
v0
a
v1
v0
a
a
v1
b
v0
a
L= (ab)n aa |n ≥0
v1
a

41. G= (V, S, v0, →)
V={v0, v1 , v2 , x, y, z}, S={x, y, z}
→: v0 →v1 v0
v0v1 → v2v0
v2v0 → xy
v2 → x
v1 → z
v0
v0
v1
v2
v0
x
y

42. v0
L= xn y zm |n ≥1, m ≥0
v0
v0
v0
v0
v1
v0
v2
v0
v0
vo
v1
v1
vo
v0
x
z
y
v1
v1
v1
v0
v0
v1
x
y
v0
v0
v2
z
z
v1
v2
v0
v2
v1
v0
v0
x
v2
y

43. Describe el lenguaje que produce la siguiente gramática
v0 →x v0 y
v0 →xy
v0
v0
x
y
x
v0
x
y
y
v0
x
v0
y
x
v0
y
x
v0
y
x
y
L= xn yn |n ≥1

44. Describe el lenguaje que produce la siguiente gramática
v0 →x yv0
v0 →xy
v0
v0
x
x
y
v0
y
x
v0
x
y
v0
x
y
x
v0
y
L= (xy)n |n ≥1
v0
x
y
y

45. Describe el lenguaje que produce la siguiente gramática
v0 →v1 v2
v1 → xv1
v1 → x
v2 → y v2
v2 →y
L= xn ym |n ≥1, m ≥1
v0
v0
v1
v1
v2
x
x
v1
y
x
v0
v0
v1
v1
x
v2
y
x
v2
y
v2
v2
v1
x
y
y
v1
x
v2
v1
x
v2
y
y

46. Generar las reglas de producción que acepte L= xn ym |n es par, m es impar
v0 →v1 v2
v1 → xxv1
v1 → xx
v2 → yy v2
v2 →y
v0
v0
v1
v2
x
x
v1
v2
y
x
x
y
y
v2
y
v0
v1
x
x
v2
v1
x
y
y
v2
y

47. L= an bn |n ≥1
v0 →a v0 b
v0 → ab
v0
a
v0
b
a
v0
a
a
v0
b
a
v0
b
a
v0
b
a
v0
b
b
b

48. L= an bm |n ≥1, m ≥1
v0 →v1 v2
v1 → av1
v1 → a
v2 → bv2
v2 →b
v0
v1
v1
v2
a
a
b
v0
v1
a
v0
v2
v1
a
b
v1
a
v2
b
v1
a
v2
b
v2
v1
a
b

49. L= an bm |n ≥1, m ≥3
v0 →v1 v2
v1 → av1
v1 → a
v2 → b v2
v2 →bbb
v0
v0
v1
v1
v2
a
v2
b
b
a
v2
v1
a
b
v1
a
v2
b
v1
a
v2
b
b
v2
b
b
b
v0
v1
b
a
a
v1
b
b

50. L= xn ym |n ≥2, m no negativo y par
v0 →v1 v2
v1 → xv1
v1 → xx
v2 → yyv2
v2 →yy
v0
v1
x
v0
v2
x
y
v1
y
x
v1
x
v0
v1
x
v2
v1
x
y
x
v1
x
v2
y
v1
y
y
v2
y
y
v2
y
x
y
v2
y
y

51. L= xn ym |n par, m positivo y non
v0 →v1 v2
v1 → xxv1
v1 → xx
v2 → yyv2
v2 →y
v0
v0
v1
v1
x
v2
x
x
x
y
x
v2
x
v1
y
y
v2
x
x
v1
y
y
x
x
v1
x
v0
v1
v2
v2
y
y
x
y
v2
y

52. Describe el lenguaje que produce la siguiente gramática
v0
v0 →a v0 b
v0 b → bw
abw →c
v0
a
a
v0
v0
b
a
v0
a
b
b
v0
b
w
b
c
b
L= an c bn |n≥0
c
w

53. Generar la gramática para los siguientes lenguajes:
L= (xy)n zn |n≥1
v0 →xyz
v0 → xyv0 z
v0
v0
x
x
y
v0
z
v0
x
y
x
y
x
v0
z
y
v0
z
x
y
z
v0
z
x
z
y
y
z

54. L= an bn cm |n≥1, m≥1
v0 →v1 v2
v1 → av1b
v1 → ab
v2 → c
v2 → v2 c
v0
v0
v1
v1
v2
a
b
a
c
v2
v1
a
b
b
v2
v2
c
v0
v1
v2
a
v1
b
a
v1
b
a
v1
b
a
b
v2
v2
v2
v2
c
c
c
c
c
c
c

55. L= xn zn |n≥2
v0 →x v0 z
v0 →xxzz
v0
v0
x
x
z
x
z
x
v0
x
z
x
v0
z
x
x
v0
v0
z
x
z
z
v0
x
z
z
z

56. L= an bm |n≥3, n≥1
v0 →v1 v2
v1 → aaa
v1 → a v1
v2 → b
v2 →b v2
v0
v0
v1
a
a
a
b
v1
v2
v1
b
a
a
v2
v1
a
v2
b
a
a
v1
b
a
v0
a
v1
v2
a
a

57. L= an bm cm |n≥1, m≥1, ñ≥0
v0 →v1 v2
v0 →v1 v2 v3
v1 → a
v2 → b
v1 → a v1
v2 →b v2
v3 →c v3
v0
v0
v1
v2
v1
a
b
a
v2
b
v2
b

58. v0
v1
a
v2
v1
a
b
v1
a
v3
v2
b
c
v3
c
v3
c
v3
c

59. UNIDAD
IV

60. UNIDAD IV
MÁQUINAS DE TURING
estado
a
b
B
v
v
v
q0
estados
q1
q2
Estado de
aceptación
cinta
B
a
b
b
B
B
Va de derecha a izquierda y viceversa
Transición (__ __ __)
leo
Lado derecha o
izquierda
estado

61. Maquina de Turing que acepta cadenas pertenecientes al ∑={a, b}
donde el primer elemento no aparece en ningún otro lado.
estado
a
b
q0
( a, D, q1 )
( b, D, q3 )
q1
( b, D, q2 )
q2
( b, D, q2 )
B
q3
( a, D, q4 )
q4
( a, D, q4 )
q5
v
( B, −, q5 )
( B, −, q5 )
v
v

62. Diseñar una Maquina de Turing que acepte el ∑={0, 1} donde las
cadenas válidas son aquellas donde el primer elemento no vuelve a
aparecer hasta el final de la cadena
estado
0
1
q0
( 0, D, q1 )
( 1, D, q4 )
q1
q2
B
( 1, D, q2 )
( 0, D, q3 )
( 1, D, q2 )
( B, −, q7)
q3
q4
( 0, D, q5 )
q5
( 0, D, q5 )
( 1, D, q6)
( B, −, q7 )
q6
q7
v
v
v

63. Diseñar una Maquina de Turing que acepte las vocales en minúscula y genere
como salida las cadenas en mayúscula.
estado
a
e
i
o
u
B
q0
(A, D,q1)
(E,D,q1)
(I,D,q1)
(O,D,q1)
(U,D,q1)
q1
(A, D,q1)
(E,D,q1)
(I,D,q1)
(O,D,q1)
(U,D,q1)
(B,−,q2)
q2
v
v
v
v
v
v
Diseñar una Maquina de Turing que acepte ∑={0,1} donde los ceros están
transformados en unos y los unos en ceros.
estado
0
1
B
q0
( 1, D, q1 )
( 0, D, q1 )
q1
( 1, D, q2 )
( 0, D, q2 )
q2
( 1, D, q2 )
( 0, D, q2 )
( B, −, q3)
q3
v
v
v

64. Diseñar una M.T que acepte cadenas pertenecientes al lenguaje
L=1n 0 1m|n≥1, m ≥1
estado
0
q0
q1
1
B
( 1, D, q1 )
( 0, D, q2 )
( 1, D, q1)
q2
( 1, D, q3 )
q3
( 1, D, q3 )
( B, −, q4)
v
v
q4
v
Diseñar una M.T que acepte cadenas pertenecientes al lenguaje
L=0n 1m|n≥1, m ≥2
estado
0
q0
( 0, D, q1 )
q1
( 0, D, q1 )
1
B
( 1, D, q2)
q2
( 1, D, q3 )
q3
( 1, D, q3 )
( B, −, q4)
v
v
q4
v

65. Diseñar una M.T que acepte ∑={0,1} donde el L=110n|n≥1
estado
0
1
B
q0
( 1, D, q1 )
q1
( 1, D, q2)
q2
( 0, D, q3 )
q3
( 0, D, q3 )
q4
v
( B, −, q4)
v
v
Diseñar una M.T que acepte ∑={0,1} donde las cadenas válidas son
aquellas que pertenecen al L=xxn yym|n≥0, m ≥1
Estado
x
q0
( x, D, q1 )
q1
( x, D, q1 )
B
( y, D, q2 )
( y, D, q2 )
q2
q3
y
v
( B, −, q4)
v
v

66. Diseñar una M.T que acepte el L=xm ynzñ|m≥1, n ≥1, ñ ≥2
estado
x
y
z
q0
( x, D, q1 )
q1
( x, D, q1 ) ( y, D, q2 )
q2
( y, D, q2 )
B
( z, D, q3)
q3
( z, D, q4 )
q4
( z, D, q4 ) ( B, −, q5)
q5
v
v
v
v
Diseñar una M.T que acepte el L=(xy)n|n ≥1,
estado
x
q0
( x, D, q1 )
q1
y
B
( y, D, q2 )
q2
q3
v
( B, −, q3 )
( x, D, q1 )
v
v

67. Diseñar una M.T que acepte el L=a(bc)n|n ≥2
estado
a
q0
( a, D, q1 )
q1
b
B
( b, D,q2 )
q2
( c, D, q3 )
q3
( b, D,q4 )
q4
( c, D, q5 )
q5
q6
c
( B, −, q6)
( b, D, q4)
v
v
v
v

68. FIN