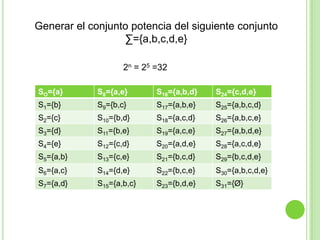
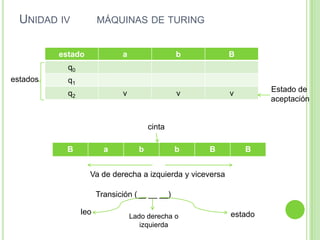
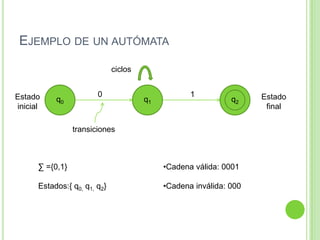
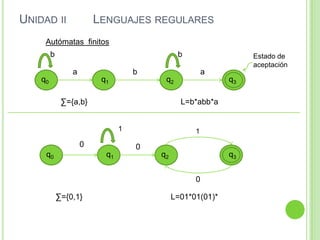
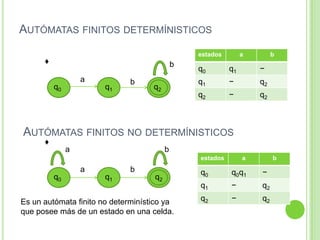
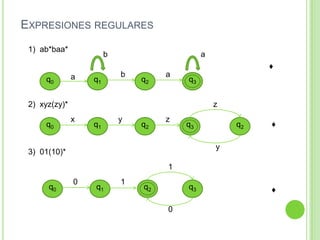
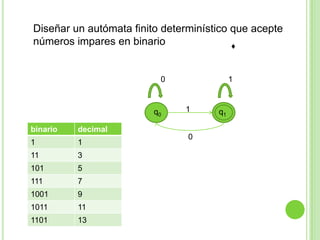
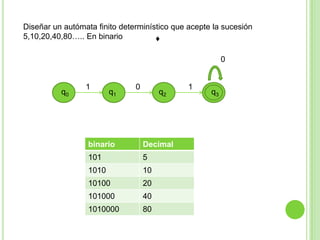
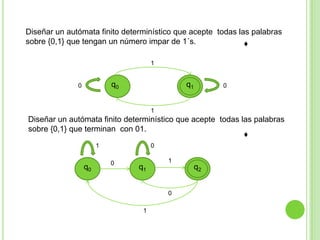
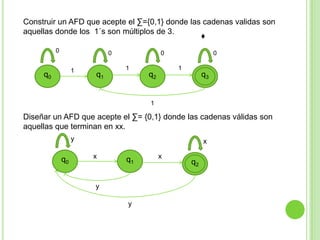
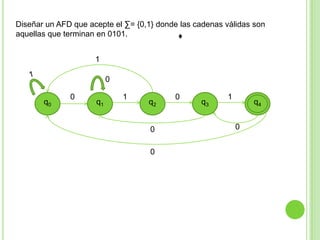
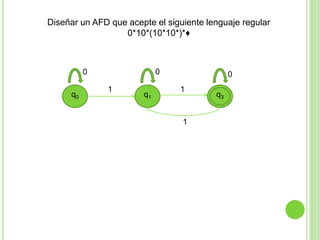
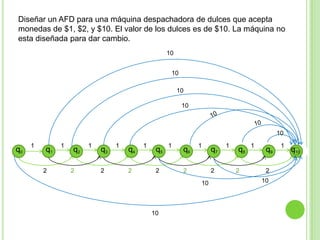
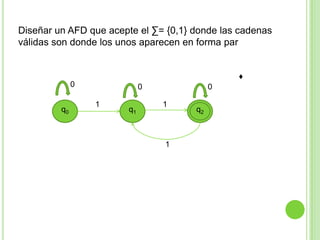
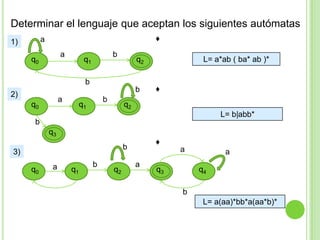
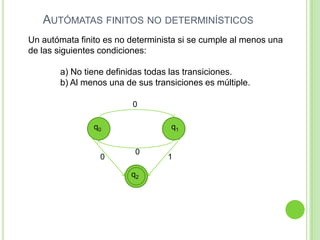
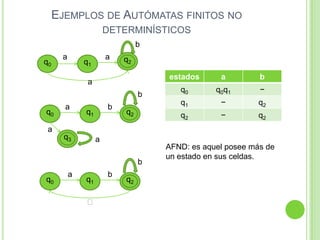
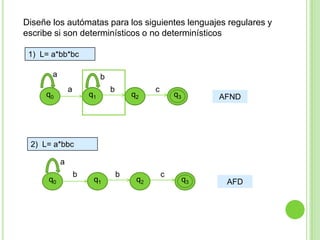
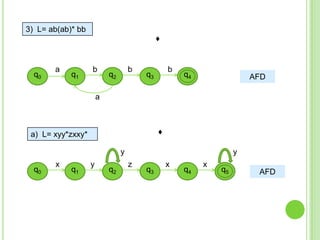
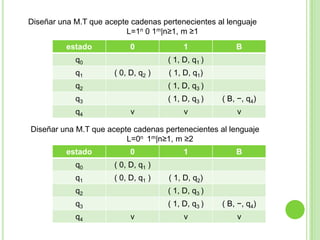
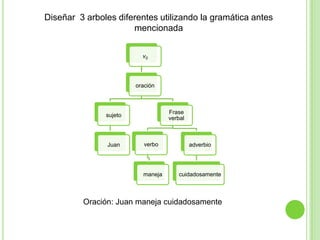
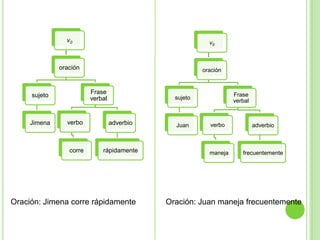
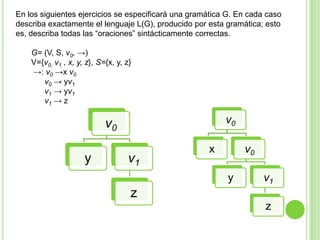
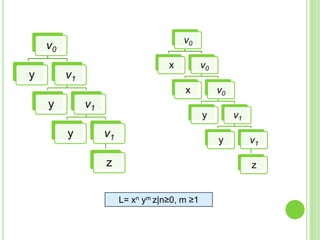
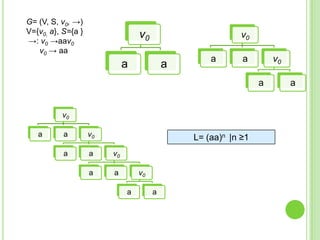
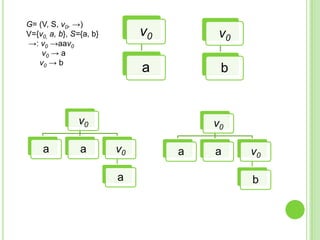
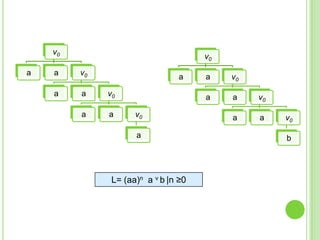
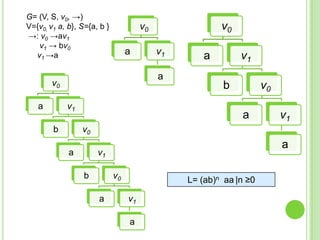
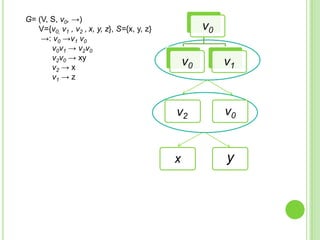
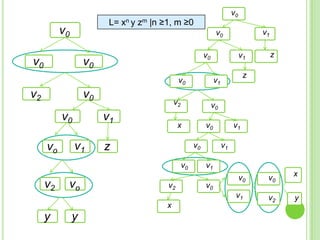
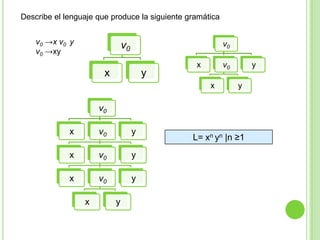
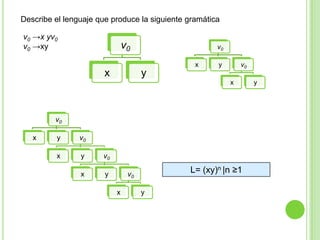
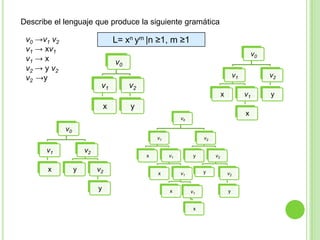
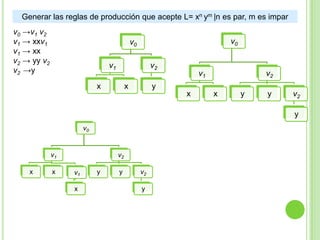
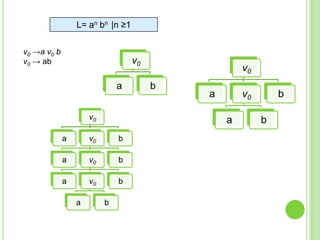
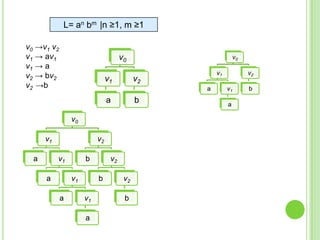
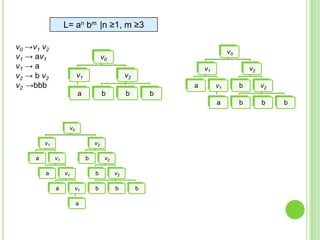
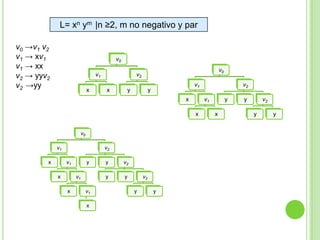
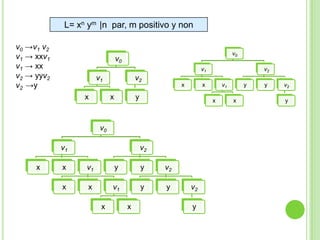
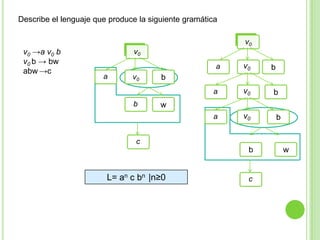
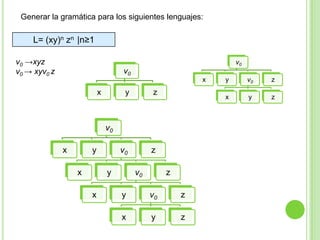
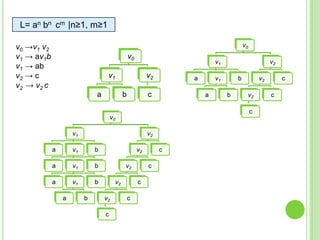
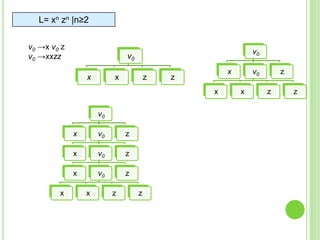
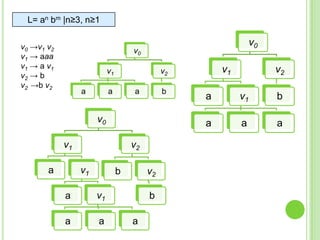
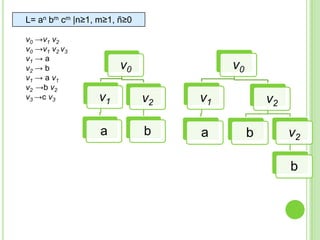
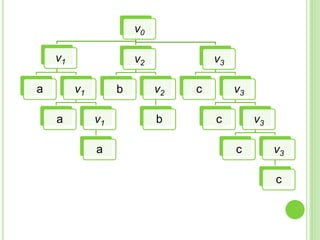
1) El documento presenta apuntes de la materia Teoría de la Computación. Introduce conceptos como conjuntos, autómatas finitos y lenguajes regulares y libres de contexto. 2) Incluye ejemplos y ejercicios para diseñar autómatas finitos determinísticos y no determinísticos que acepten diferentes lenguajes regulares. 3) Explica gramáticas formales y cómo generar los árboles sintácticos y lenguajes producidos por diferentes gramáticas dadas.

1. INSTITUTO TECNOLÓGICO DE TUXTEPEC Materia: teoría de la computación catedrático: Olivia Guadalupe López Ruíz Apuntes de la materia

2. UNIDAD I

3. conjuntos Definición: Un conjunto es un grupo o colección de objetos, a los que se le conoce como elementos o miembros del mismo. Notación: Una forma de describir un conjunto con un numero finito de elementos, es hacer una lista de elementos del conjunto y encerrarla entre llaves. Ejemplo , el conjunto de todos lo enteros positivos menores que 4. A={1, 2 ,3 } En cambio para representar un conjunto infinito utilizando la se requiere hacer uso de la notación P(x), para denotar una oración o enunciado P relativo al objeto variable x. El objeto definido por P(x), escrito en la forma {x|P(x)} es simplemente la colección de todos los objetos x para los cuales P es sensible y cierto. Ejemplo: A={x| x es un entero positivo}

4. Conjunto potencia Definición: El conjunto potencia es aquel que contiene todos los subconjuntos de un conjunto original. Para obtenerlo se utiliza la formula 2n donde n indica el número de elementos del conjunto. Ejemplos: A={a,b,c} 2n = 23 =8 subconjuntos

5. Determinar todos los subconjuntos que se generan del conjunto A={0,1,2,3} 2n = 24 =16

6. Generar el conjunto potencia del siguiente conjunto ∑={a,b,c,d,e} 2n = 25 =32

7. Cadenas Definición: Una cadena (string) de caracteres es un conjunto de caracteres(incluido el blanco, que se almacenan en un área continua de memoria. Longitud de cadena: Es el número de caracteres que contiene la cadena.la cadena que no contiene ningún carácter se denomina nula o vacía. Concatenación de cadenas: Es la operación de reunir varias cadenas de caracteres en una sola, conservando el orden de sus caracteres.

8. Forma de representar los conceptos estudiados anteriormente: Reverso xr=ejaugnel yr=auga zr=acnalb ar=ojor br=noicamargorp cr=321 Cadenas x=lenguaje y=agua z=blanca a=rojo b=programacion c=123 Longitud |lenguaje | =8 | agua | =4 | blanca | =6 | rojo | =4 | Programacion | =12 | 123 | =3 Concatenación y . z= aguablanca x . b= lenguajeprogramacion

9. Autómatas Autómata: Es una máquina formal que acepta un alfabeto de entrada y produce una salida, es decir, una máquina que valida cadenas y verifica si son válidas o inválidas. Los autómatas se clasifican en: -Finitos determinísticos -Finitos no determinísticos

12. Unidad ii Lenguajes regulares Autómatas finitos b b Estado de aceptación a b a q3 q2 q1 q0 ∑={a,b} L=b*abb*a 1 1 0 0 q0 q3 q2 q1 q3 0 ∑={0,1} L=01*01(01)*

13. Diseñar un autómata finito que acepte el ∑={0,1} donde las cadenas validas son aquellas que pertenecen a la sucesión 10, 20,,30 ,40,80 160… en binario 0 1 0 1 0 q0 q2 q1 q3 q4

14. Autómatas finitos determínisticos ♦ b a b q0 q2 q1 Autómatas finitos no determínisticos ♦ a b a b q0 q1 q2 Es un autómata finito no determinístico ya que posee más de un estado en una celda.

15. Expresiones regulares 1) ab*baa* b a ♦ b a a q0 q1 q2 q3 2) xyz(zy)* z x y z ♦ q0 q1 q2 q3 q3 q2 y 3) 01(10)* 1 0 1 q0 q1 q3 q2 ♦ 0

16. Diseñar un autómata finito determinístico que acepte números impares en binario ♦ 0 1 1 q0 q1 0

17. Diseñar un autómata finito determinístico que acepte la sucesión 5,10,20,40,80….. En binario ♦ 0 1 0 1 q2 q1 q0 q3

18. Diseñar un autómata finito determinístico que acepte todas las palabras sobre {0,1} que tengan un número impar de 1´s. ♦ 1 q0 q1 0 0 1 Diseñar un autómata finito determinístico que acepte todas las palabras sobre {0,1} que terminan con 01. ♦ 1 0 1 0 q0 q1 q2 0 1

19. Construir un AFD que acepte el ∑={0,1} donde las cadenas validas son aquellas donde los 1´s son múltiplos de 3. ♦ 0 0 0 0 1 1 1 q2 q1 q0 q3 1 Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas válidas son aquellas que terminan en xx. y x x x q0 q1 q2 y y

20. Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas válidas son aquellas que terminan en 0101. ♦ 1 1 0 1 1 0 0 q3 q2 q1 q0 q4 0 0 0

21. Diseñar un AFD que acepte el siguiente lenguaje regular 0*10*(10*10*)*♦ 0 0 0 1 1 q1 q0 q3 1

22. Diseñar un AFD para una máquina despachadora de dulces que acepta monedas de $1, $2, y $10. El valor de los dulces es de $10. La máquina no esta diseñada para dar cambio. 10 10 10 10 10 10 10 1 1 1 1 1 1 1 1 1 1 q0 q1 q2 q3 q6 q5 q4 q8 q7 q9 q10 2 2 2 2 2 2 2 2 2 10 10 10

23. Diseñar un AFD que acepte el ∑= {0,1} donde las cadenas válidas son donde los unos aparecen en forma par ♦ 0 0 0 1 1 q1 q0 q2 1

24. Determinar el lenguaje que aceptan los siguientes autómatas ♦ a 1) b a q0 q1 L= a*ab ( ba* ab )* q2 b ♦ b 2) a b q0 q1 q2 L= b|abb* b q3 ♦ b a 3) a a b a q0 q1 q3 q2 q4 b L= a(aa)*bb*a(aa*b)*

25. Autómatas finitos no determinísticos Un autómata finito es no determinista si se cumple al menos una de las siguientes condiciones: a) No tiene definidas todas las transiciones. b) Al menos una de sus transiciones es múltiple. 0 q0 q1 0 1 0 q2

26. Ejemplos de Autómatas finitos no determinísticos b a a q2 q0 q1 a b a b q0 q1 q2 a q3 a AFND: es aquel posee más de un estado en sus celdas. b a b q0 q1 q2 

27. Diseñe los autómatas para los siguientes lenguajes regulares y escribe si son determinísticos o no determinísticos 1) L= a*bb*bc a b a b c q0 q1 q3 q2 AFND 2) L= a*bbc a b b c q0 q1 q2 q3 AFD

28. 3) L= ab(ab)* bb ♦ a b b b q0 q1 q2 q3 q4 AFD a ♦ a) L= xyy*zxxy* y y x y z x x q0 q1 q2 q3 q4 q5 AFD

29. Unidad iii

30. Unidad iii lenguajes libres de contexto Gramática(G): una gramática se define por una 4-ada (V, S, v0, ->) Gramática= (V, S, v0, ->) Donde: V= Todas las cadenas permitidas S= Subconjunto de todas las cadenas permitidas v0= Inicio ->= Reglas de producción

32. símbolos no terminales; siguen produciendo algo.S={Juan, Jimena, maneja, corre, cuidadosamente, rápidamente, frecuentemente} N={oración, sujeto, frase verbal, verbo, adverbio} V= S U N V={Juan, Jimena, maneja, corre, cuidadosamente, rápidamente, frecuentemente, oración, sujeto, frase verbal, verbo, adverbio} v0= “oración” ->= todas las posibles combinaciones que la gramática permite

33. Oración -> sujeto frase verbal Sujeto -> juan Sujeto -> jimena Frase verbal -> verbo adverbio verbo -> maneja verbo ->corre adverbio -> cuidadosamente adverbio -> rapidamente adverbio -> frecuentemente El conjunto de todas las oraciones bien construidas que puede producirse al usar una gramática G, se llama lenguaje de G y se escribe L(G).

34. Diseñar 3 arboles diferentes utilizando la gramática antes mencionada Oración: Juan maneja cuidadosamente

35. Oración: Jimena corre rápidamente Oración: Juan maneja frecuentemente

36. En los siguientes ejercicios se especificará una gramática G. En cada caso describa exactamente el lenguaje L(G), producido por esta gramática; esto es, describa todas las “oraciones” sintácticamente correctas. G= (V, S, v0, ->) V={v0,v1 , x, y, z}, S={x, y, z} ->: v0 ->x v0 v0 -> yv1 v1 -> yv1 v1 -> z

37. L= xnymz|n≥0, m ≥1

38. G= (V, S, v0, ->) V={v0, a}, S={a } ->: v0 ->aav0 v0 -> aa L= (aa)n|n ≥1

39. G= (V, S, v0, ->) V={v0, a, b}, S={a, b} ->: v0 ->aav0 v0 -> a v0 -> b

40. L= (aa)n a v b|n ≥0

41. G= (V, S, v0, ->) V={v0, v1 a, b}, S={a, b } ->: v0 ->av1 v1 -> bv0 v1->a L= (ab)naa|n ≥0

42. G= (V, S, v0, ->) V={v0,v1 , v2 ,x, y, z}, S={x, y, z} ->: v0 ->v1 v0 v0v1 -> v2v0 v2v0 -> xy v2 -> x v1 -> z v0 x v2 y

43. v2 v1 v1 z v0 v0 v1 v0 z v0 v1 v0 x v1 v0 v0 v1 v0 v1 v2 v0 x v0 v1 v0 v2 x y v0 v0 v0 v2 v0 v0 v1 z vo v2 vo y y L= xny zm |n ≥1, m ≥0

44. Describe el lenguaje que produce la siguiente gramática v0 ->x v0 y v0 ->xy L= xnyn |n ≥1

45. Describe el lenguaje que produce la siguiente gramática v0 ->x yv0 v0 ->xy L= (xy)n |n ≥1

46. Describe el lenguaje que produce la siguiente gramática v0 ->v1 v2 v1-> xv1 v1 -> x v2 -> y v2 v2 ->y L= xnym|n ≥1, m ≥1

47. Generar las reglas de producción que acepte L= xnym|n es par, m es impar v0 ->v1 v2 v1-> xxv1 v1 -> xx v2 -> yy v2 v2 ->y

48. L= anbn|n ≥1 v0 ->a v0 b v0-> ab

49. L= anbm|n ≥1, m ≥1 v0 ->v1 v2 v1-> av1 v1 -> a v2 -> bv2 v2 ->b

50. L= anbm|n ≥1, m ≥3 v0 ->v1 v2 v1-> av1 v1 -> a v2 -> b v2 v2 ->bbb

51. L= xnym|n ≥2, m no negativo y par v0 ->v1 v2 v1-> xv1 v1 -> xx v2 -> yyv2 v2 ->yy

52. L= xnym|n par, m positivo y non v0 ->v1 v2 v1-> xxv1 v1 -> xx v2 -> yyv2 v2 ->y

53. v0 a b c a b a b a b c Describe el lenguaje que produce la siguiente gramática v0 ->a v0 b v0 b-> bw abw->c v0 b v0 w v0 b w L= an c bn|n≥0

54. Generar la gramática para los siguientes lenguajes: L= (xy)nzn|n≥1 v0 ->xyz v0 -> xyv0 z

55. L= anbn cm |n≥1, m≥1 v0 ->v1 v2 v1-> av1b v1 -> ab v2 -> c v2 -> v2 c

56. L= xnzn |n≥2 v0 ->x v0z v0 ->xxzz

57. L= anbm |n≥3, n≥1 v0 ->v1 v2 v1-> aaa v1 -> av1 v2 -> b v2 ->bv2

58. L= anbm cm |n≥1, m≥1, ñ≥0 v0 ->v1v2 v0 ->v1v2v3 v1-> a v2 -> b v1 -> av1 v2 ->bv2 v3->cv3

60. Unidadiv

61. Unidad iv máquinas de turing estados Estado de aceptación cinta Va de derecha a izquierda y viceversa Transición (__ __ __) leo estado Lado derecha o izquierda

62. Maquina de Turing que acepta cadenas pertenecientes al ∑={a, b} donde el primer elemento no aparece en ningún otro lado.

63. Diseñar una Maquina de Turing que acepte el ∑={0, 1} donde las cadenas válidas son aquellas donde el primer elemento no vuelve a aparecer hasta el final de la cadena

64. Diseñar una Maquina de Turing que acepte las vocales en minúscula y genere como salida las cadenas en mayúscula. Diseñar una Maquina de Turing que acepte ∑={0,1} donde los ceros están transformados en unos y los unos en ceros.

65. Diseñar una M.T que acepte cadenas pertenecientes al lenguaje L=1n 0 1m|n≥1, m ≥1 Diseñar una M.T que acepte cadenas pertenecientes al lenguaje L=0n 1m|n≥1, m ≥2

66. Diseñar una M.T que acepte ∑={0,1} donde el L=110n|n≥1 Diseñar una M.T que acepte ∑={0,1} donde las cadenas válidas son aquellas que pertenecen al L=xxn yym|n≥0, m ≥1

67. Diseñar una M.T que acepte el L=xm ynzñ|m≥1, n ≥1, ñ ≥2 Diseñar una M.T que acepte el L=(xy)n|n ≥1,

68. Diseñar una M.T que acepte el L=a(bc)n|n ≥2

69. FIN