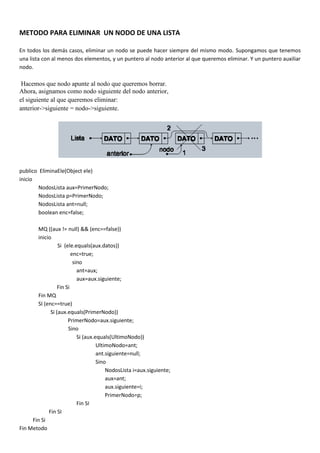
Las listas enlazadas son estructuras de datos dinámicas en las que cada nodo apunta al siguiente. Existen listas simples, doblemente enlazadas y circulares. Las listas permiten insertar nodos de forma dinámica y recorrerlos de forma secuencial, a diferencia de los arrays donde el acceso es aleatorio pero la inserción requiere redimensionar.

1. LISTAS
Las listas enlazadas son estructuras de datos semejantes a los array salvo que el acceso a un elemento no se hace
mediante un indice sino mediante un puntero.
La asignación de memoria es hecha durante la ejecución.
Listas simples enlazadas
La lista enlazada básica es la lista enlazada simple la cual tiene un enlace por nodo. Este enlace apunta al
siguiente nodo en la lista, o al valor NULL o a la lista vacía, si es el último nodo.
Una lista enlazada simple contiene dos valores: el valor actual del nodo y un enlace al siguiente nodo
Lista Doblemente Enlazada
Un tipo de lista enlazada más sofisticado es la lista doblemente enlazada o lista enlazadas de dos vías.
Cada nodo tiene dos enlaces: uno apunta al nodo anterior, o apunta al valor NULL si es el primer nodo; y
otro que apunta al nodo siguiente, o apunta al valor NULL si es el último nodo.
Una lista doblemente enlazada contiene tres valores: el valor, el link al nodo siguiente, y el link al anterior
Listas enlazadas circulares
En una lista enlazada circular, el primer y el último nodo están unidos juntos. Esto se puede hacer tanto para
listas enlazadas simples como para las doblemente enlazadas. Para recorrer una lista enlazada circular
podemos empezar por cualquier nodo y seguir la lista en cualquier dirección hasta que se regrese hasta el
nodo original. Desde otro punto de vista, las listas enlazadas circulares pueden ser vistas como listas sin
comienzo ni fin. Este tipo de listas es el más usado para dirigir buffers para “ingerir” datos, y para visitar
todos los nodos de una lista a partir de uno dado.
Una lista enlazada circular que contiene tres valores enteros
Listas Enlazadas vs. Vectores o Matrices

2. Las listas enlazadas poseen muchas ventajas sobre los arrays. Los elementos se pueden insertar en una lista
indefinidamente mientras que un array tarde o temprano se llenará ó necesitará ser redimensionado, una
costosa operación que incluso puede no ser posible si la memoria se encuentra fragmentada.
En algunos casos se pueden lograr ahorros de memoria almacenando la misma „cola‟ de elementos entre dos
o más listas – es decir, la lista acaba en la misma secuencia de elementos. De este modo, uno puede añadir
nuevos elementos al frente de la lista manteniendo una referencia tanto al nuevo como a los viejos elementos
- un ejemplo simple de una estructura de datos persistente.
Por otra parte, los arrays permiten acceso aleatorio mientras que las listas enlazadas sólo permiten acceso
secuencial a los elementos. Las listas enlazadas simples, de hecho, solo pueden ser recorridas en una
dirección. Esto hace que las listas sean inadecuadas para aquellos casos en los que es útil buscar un
elementos por su índice rápidamente, como el heapsort. El acceso secuencial en los arrays también es más
rápido que en las listas enlazadas.
Otra desventaja de las listas enlazadas es el almacenamiento extra necesario para las referencias, que a
menudos las hacen poco prácticas para listas de pequeños datos como caracteres o valores booleanos.
También puede resultar lento y abusivo el asignar memoria para cada nuevo elemento. Existe una variedad
de listas enlazadas que contemplan los problemas anteriores para resolver los mismos. Un buen ejemplo que
muestra los pros y contras del uso de arrays sobre listas enlazadas es la implementación de un programa que
resuelva el problema de Josephus. Este problema consiste en un grupo de personas dispuestas en forma de
círculo. Se empieza a partir de una persona predeterminadas y se cuenta n veces, la persona n-ésima se saca
del círculo y se vuelve a cerrar el grupo. Este proceso se repite hasta que queda una sola persona, que es la
que gana. Este ejemplo muestra las fuerzas y debilidades de las listas enlazadas frente a los arrays, ya que
viendo a la gente como nodos conectados entre sí en una lista circular se observa como es más fácil suprimir
estos nodos. Sin embargo, se ve como la lista perderá utilidad cuando haya que encontrar a la siguiente
persona a borrar. Por otro lado, en un array el suprimir los nodos será costoso ya que no se puede quitar un
elemento sin reorganizar el resto. Pero en la búsqueda de la n-ésima persona tan sólo basta con indicar el
índice n para acceder a él resultando mucho más eficiente.
LISTAS SIMPLES

3. La forma más simple de estructura dinámica es la lista Simple. En esta forma los nodos se organizan de
modo que cada uno apunta al siguiente, y el último no apunta a nada, es decir, el puntero del nodo siguiente
vale NULL.
En las listas abiertas existe un nodo especial: el primero. Normalmente diremos que nuestra lista es un
puntero a ese primer nodo y llamaremos a ese nodo la cabeza de la lista. Eso es porque mediante ese único
puntero podemos acceder a toda la lista.
Cuando el puntero que usamos para acceder a la lista vale NULL, diremos que la lista está vacía.
TIPS!!!!!!!!!!!!!!!!!!!!!!!
Sólo hay un modo de moverse a través de una lista
Simple……hacia delante!!.
El primer elemento es el más accesible, ya que es a
ese a que apunta el puntero que define la lista. Para
obtener un puntero al primer elemento bastará con
copiar el puntero Lista.
Supongamos que tenemos un puntero nodo que
señala a un elemento de una lista. Para obtener un
puntero al siguiente bastará con asignarle el campo
"siguiente" del nodo, nodo->siguiente.
Ya hemos dicho que no es posible retroceder en una
lista, de modo que para obtener un puntero al nodo
anterior a uno dado tendremos que partir del
primero, e ir avanzando hasta que el nodo siguiente
sea precisamente el nodo buscado.
Para obtener un puntero al último elemento de una
lista partiremos de un nodo cualquiera, por ejemplo el

4. primero, y avanzaremos hasta que su nodo siguiente
sea NULL.
Basta con comparar el puntero Lista con NULL, si Lista
vale NULL la lista está vacía.
El algoritmo genérico para borrar una lista completa
consiste simplemente en borrar el primer elemento
sucesivamente mientras la lista no esté vacía.
Con las listas tendremos un pequeño repertorio de operaciones básicas que se pueden realizar:
Añadir o insertar elementos.
Buscar o localizar elementos.
Borrar elementos.
Moverse a través de una lista, siguiente, primero.
Cada una de estas operaciones tendrá varios casos especiales, por ejemplo, no será lo mismo insertar un
nodo en una lista vacía, o al principio de una lista no vacía, o la final, o en una posición intermedia.

5. DEFINICION
El nodo típico para construir listas tiene esta forma:
Clase NodosLista
Inicio
Object datos;
NodosLista siguiente;
// datos:: que almacena la información // siguiente : Apuntador o enlace a otros nodos
NodosLista(Object valor)
Inicio
datos=valor;//
siguiente=null;//
Fin
//--Constructor Crea un nodo de tipo Object y al siguiente nodo de la lista --//
NodosLista (Object valor,NodosLista signodo)
// parámetro valor capturado en método principal y signodo para ligar el puntero a la ultima posición
Inicio
datos=valor;// Se asigna el valor digitado en el campo de datos
siguiente=signodo; //siguiente se refiere al siguiente nodo
Fin
//Retorna el dato que se encuentra en ese nodo
Object getObject()
Inicio
return datos;
Fin
//Retorna el siguiente nodo
NodosLista getnext()
Inicio
return siguiente;
Fin
Fin
NodosLista es el tipo para declarar listas, como puede verse, un puntero a un nodo y una lista son la misma cosa. En
realidad, cualquier puntero a un nodo es una lista, cuyo primer elemento es el nodo apuntado.

6. DEFINICION DE LA CLASE LISTA
clase ListaSimple
inicio
NodosLista PrimerNodo;// se define el primer nodo de la lista
NodosLista UltimoNodo;// se define el ultimo nodo de la lista
String Nombre;// variable de tipo string para almacenar dato
METODOS ASOCIADOS
METODO PARA DETERMINAR SI UNA LISTA ESTA VACIA
publico booleano VaciaLista()
Inicio
Retornar PrimerNodo ==null; // si el primer nodo apunta a null esta vacia
fin
METODO PARA INSERTAR UN NODO EN UNA LISTA VACIA
Este es, evidentemente, el caso más sencillo. Partiremos de que ya tenemos el nodo a insertar y, por supuesto
un puntero que apunte a la lista valdrá NULL:
publico ListaSimple(cadena s) // el valor que se captura en menú para el primer nodo
inicio
Nombre=s;
PrimerNodo=UltimoNodo=null;
// tanto el primero como ultimo se apunta a null esto determina unico dato capturado en S pero se para a var Nombre
Fin
Podemos considerar el caso anterior como un caso particular de éste, la única diferencia es que en el caso
anterior la lista es una lista vacía, pero siempre podemos, y debemos considerar una lista vacía como una
lista.

7. METODO PARA INSERTAR UN NODO AL PRINCIPIO DE UNA LISTA
De nuevo partiremos de un nodo a insertar, con un puntero que apunte a él, y de una lista, en este caso no
vacía:
El proceso sigue siendo muy sencillo:
1. Hacemos que el nodo->siguiente apunte a Lista.
2. Hacemos que Lista apunte a nodo.
Publico InsertaInicio(Object ElemInser)
Inicio
Si(VaciaLista()) // se verifica contenido en la lista
PrimerNodo=UltimoNodo=new NodosLista(ElemInser);
sino
PrimerNodo=new NodosLista(ElemInser, PrimerNodo);
Fin
Nota: Ojo con la definición de los nodos y verificar los parámetros, incentivo para el estudiante que identifique lo
sucedido en el método insertar al inicio.

8. METODO PARA INSERTAR UN NODO AL FINAL DE UNA LISTA
Este es otro caso especial. Para este caso partiremos de una lista no vacía:
El proceso en este caso tampoco es excesivamente complicado:
1. Necesitamos un puntero que señale al último elemento de la lista. Se nombro al inicio de la clase un
nodo con el nombre de UltimoNodo.
2. Hacer que nodo->siguiente sea NULL.
3. Hacer que ultimo->siguiente sea nodo.
publico InsertaFinal(Object ElemInser)
Inicio
si(VaciaLista()) // se verifica contenido en la lista
PrimerNodo= UltimoNodo = new NodosLista (ElemInser);
sino
UltimoNodo=UltimoNodo.siguiente=new NodosLista(ElemInser);
Fin Si
Fin Método

9. METODO PARA RECORRER Y MOSTRAR LOS ELEMENTOS DE UNA LISTA
Se indico que las listas simples elaboran el recorrido desde el principio de la lista al final de la misma, por lo cual se
crea un nodo auxiliar llamado Actual que almacena temporalmente el principio de la lista y es el encargado de
realizar dicho recorrido hasta que tenga el valor de null.
Publico Imprimir()
Inicio
Si (VaciaLista())
Inicio
System.out.println("Vacia" + Nombre);
Sino
Escriba ("La "+Nombre + " es: ");
NodosLista Actual=PrimerNodo;
MQ (Actual != null
Escriba (Actual.datos.toString()+" ");
Actual=Actual.siguiente;// se hace referencia al siguiente nodo
Fin MQ
Fin Si
Fin Método

10. METODO PARA ELIMINAR UN NODO DE UNA LISTA
En todos los demás casos, eliminar un nodo se puede hacer siempre del mismo modo. Supongamos que tenemos
una lista con al menos dos elementos, y un puntero al nodo anterior al que queremos eliminar. Y un puntero auxiliar
nodo.
Hacemos que nodo apunte al nodo que queremos borrar.
Ahora, asignamos como nodo siguiente del nodo anterior,
el siguiente al que queremos eliminar:
anterior->siguiente = nodo->siguiente.
publico EliminaEle(Object ele)
inicio
NodosLista aux=PrimerNodo;
NodosLista p=PrimerNodo;
NodosLista ant=null;
boolean enc=false;
MQ ((aux != null) && (enc==false))
inicio
Si (ele.equals(aux.datos))
enc=true;
sino
ant=aux;
aux=aux.siguiente;
Fin Si
Fin MQ
SI (enc==true)
Si (aux.equals(PrimerNodo))
PrimerNodo=aux.siguiente;
Sino
Si (aux.equals(UltimoNodo))
UltimoNodo=ant;
ant.siguiente=null;
Sino
NodosLista i=aux.siguiente;
aux=ant;
aux.siguiente=i;
PrimerNodo=p;
Fin SI
Fin SI
Fin Si
Fin Metodo