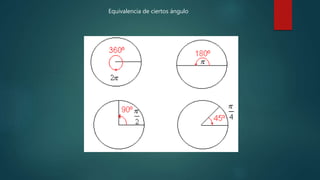
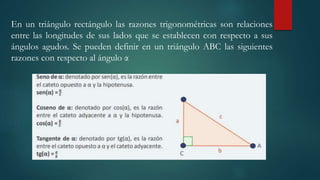
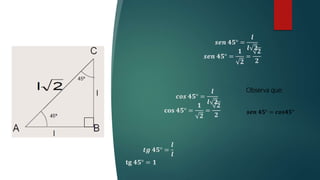
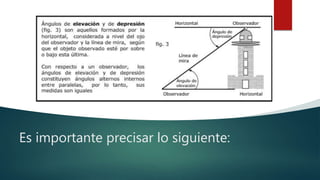
La unidad introduce conceptos básicos de trigonometría como grados, radianes y conversiones entre ellos. Explica que las razones trigonométricas son relaciones entre los lados de un triángulo rectángulo con respecto a sus ángulos agudos, y proporciona los valores de sen, cos y tg para ángulos de 30°, 45° y 60° utilizando triángulos equiláteros y cuadrados. Finalmente enfatiza la importancia de las identidades trigonométricas.