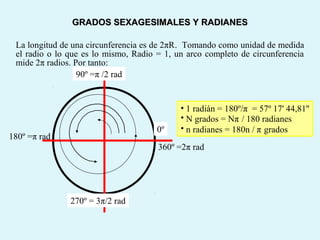
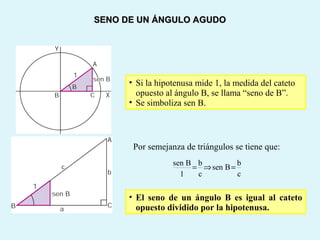
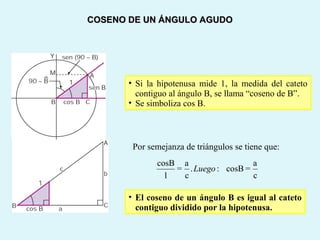
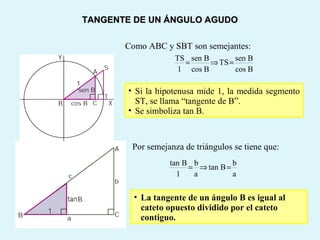
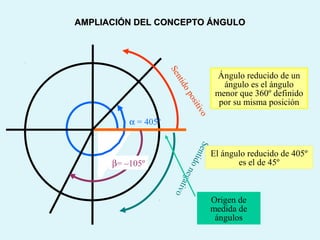
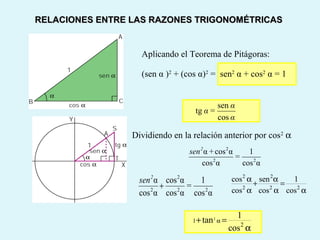
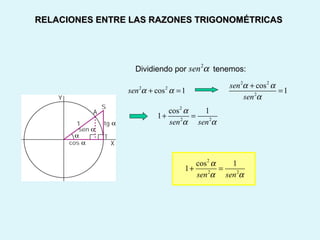
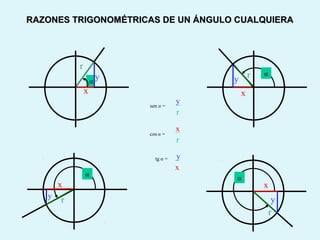
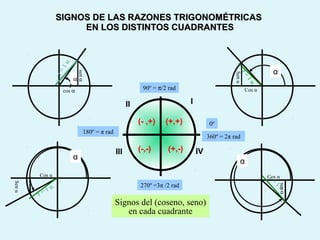
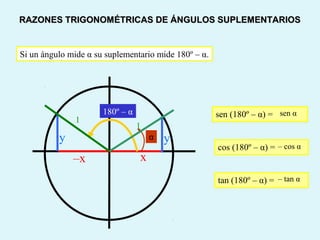
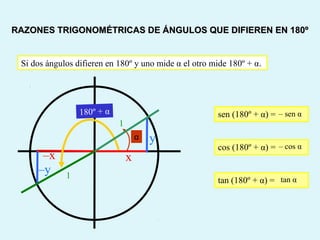
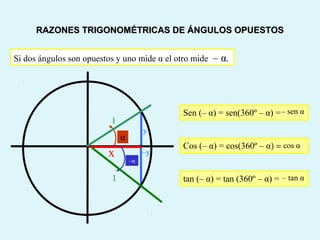
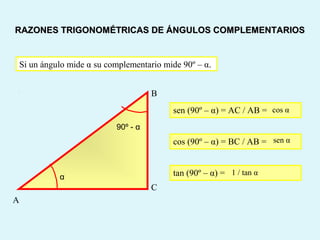
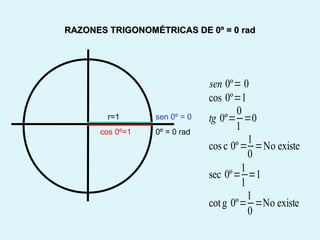
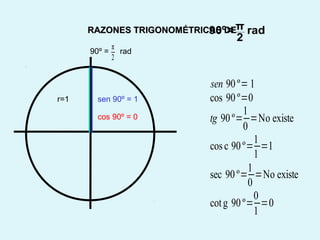
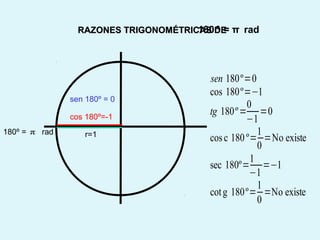
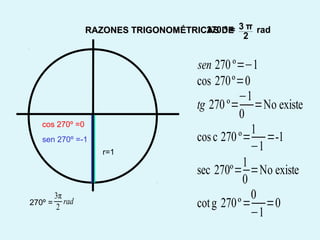
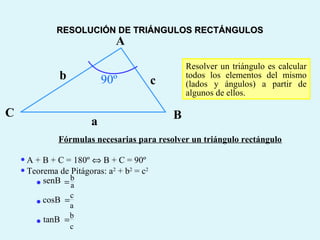
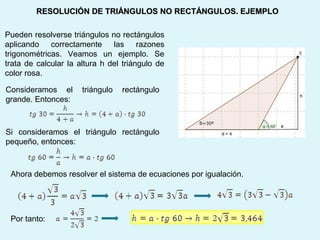
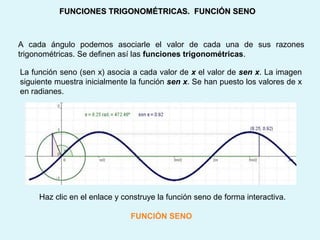
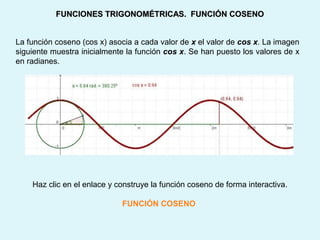
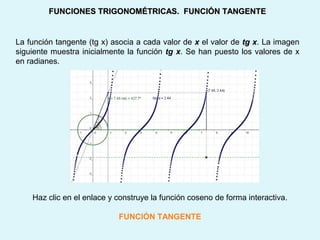
Este documento presenta los conceptos básicos de la trigonometría, incluyendo las definiciones de seno, coseno y tangente para ángulos agudos y obtusos. También explica las relaciones entre las funciones trigonométricas y cómo calcular ángulos y lados en triángulos rectángulos y no rectángulos.

1. APM

2. • Historia de la Trigonometría.
•Grados sexagesimales y radianes.
• Seno de un ángulo agudo.
• Coseno de un ángulo agudo.
• Tangente de un ángulo agudo.
• Ampliación del concepto de ángulo.
• Relaciones entre las razones trigonométricas.
• Razones trigonométricas de un ángulo cualquiera.
• Signos de las razones trigonométricas en los distintos cuadrantes.
• Razones trigonométricas de ángulos suplementarios.
• Razones trigonométricas de ángulos que difieren en 180º.
• Razones trigonométricas de ángulos opuestos.
• Razones trigonométricas de ángulos complementarios.
• Razones trigonométricas de 0º.
• Razones trigonométricas de 90º.
• Razones trigonométricas de 180º.
• Razones trigonométricas de 270º.
• Resolución de triángulos rectángulos.
• Ejemplo de resolución de triángulo rectángulo.
• Resolución de triángulos no rectángulos. Ejemplo.
• Funciones trigonométricas. Función seno.
• Función coseno.
• Función tangente.
INTRODUCCIÓN A LA TRIGONOMETRÍA. ÍNDICEINTRODUCCIÓN A LA TRIGONOMETRÍA. ÍNDICE

3. La Trigonometría es la parte de las Matemáticas que se encarga del estudio de
las relaciones que existen entre los ángulos y los lados de un triángulo. Estas
relaciones se aplican para resolver muchas situaciones de la vida cotidiana.
HISTORIA DE LA TRIGONOMETRÍAHISTORIA DE LA TRIGONOMETRÍA
La Trigonometría es una rama de la matemática, cuyo significado etimológico es
“la medición de los triángulos”.
Se deriva del vocablo griego:
τριγωνο <trigōno> “triángulo” + μετρον <metron> “medida”.
Si quieres saber más sobre la historia y aparición de la Trigonometría, puedes
acceder a la presentación titulada: HISTORIA DE LA TRIGONOMETRÍA.

4. 0º
90º =π /2 rad
180º =π rad
270º = 3π/2 rad
360º =2π rad
La longitud de una circunferencia es de 2πR. Tomando como unidad de medida
el radio o lo que es lo mismo, Radio = 1, un arco completo de circunferencia
mide 2π radios. Por tanto:
• 1 radián = 180º/π = 57º 17' 44,81''
• N grados = Nπ / 180 radianes
• n radianes = 180n / π grados
GRADOS SEXAGESIMALES Y RADIANESGRADOS SEXAGESIMALES Y RADIANES

5. • Si la hipotenusa mide 1, la medida del cateto
opuesto al ángulo B, se llama “seno de B”.
• Se simboliza sen B.
Por semejanza de triángulos se tiene que:
• El seno de un ángulo B es igual al cateto
opuesto dividido por la hipotenusa.
SENO DE UN ÁNGULO AGUDOSENO DE UN ÁNGULO AGUDO
sen B b b
sen B
1 c c
= ⇒ =

6. • Si la hipotenusa mide 1, la medida del cateto
contiguo al ángulo B, se llama “coseno de B”.
• Se simboliza cos B.
Por semejanza de triángulos se tiene que:
• El coseno de un ángulo B es igual al cateto
contiguo dividido por la hipotenusa.
c
a
cosB:.
c
a
1
cosB
=Luego=
COSENO DE UN ÁNGULO AGUDOCOSENO DE UN ÁNGULO AGUDO

7. • Si la hipotenusa mide 1, la medida segmento
ST, se llama “tangente de B”.
• Se simboliza tan B.
Por semejanza de triángulos se tiene que:
tan B b b
tan B
1 a a
= ⇒ =
• La tangente de un ángulo B es igual al
cateto opuesto dividido por el cateto
contiguo.
Como ABC y SBT son semejantes:
TS sen B sen B
TS
1 cos B cos B
= ⇒ =
TANGENTE DE UN ÁNGULO AGUDOTANGENTE DE UN ÁNGULO AGUDO

8. Sentidonegativo
Origen de
medida de
ángulos
α = 405º
β= –105º
Sentidopositivo
Ángulo reducido de un
ángulo es el ángulo
menor que 360º definido
por su misma posición
El ángulo reducido de 405º
es el de 45º
AMPLIACIÓN DEL CONCEPTO ÁNGULOAMPLIACIÓN DEL CONCEPTO ÁNGULO

9. Aplicando el Teorema de Pitágoras:
(sen α )2
+ (cos α)2
= sen2
α + cos2
α = 1
Dividiendo en la relación anterior por cos2
α
2 2
2 2 2
cos sen 1
cos cos cos
α α
+ =
α α α
2
1
2
1
tan
cos
α+ =
α
αcos
1
αcos
αcosα
22
2
=
+sen2
αcos
1
αcos
αcos
αcos
α
22
2
2
=
sen2
+
RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICASRELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS
α
α
=α
cos
sen
tg

10. Dividiendo por tenemos:
2
sen α
2 2
cos 1sen α α+ =
2 2
2
cos
1
sen
sen
α α
α
+
=
2
2 2
cos 1
1
sen sen
α
α α
+ =
RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICASRELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS
2
2 2
cos 1
1
sen sen
α
α α
+ =

11. α
y y
y y
x
x x
r
r
r
α
α
α
r
x
r
y
r
x
x
y
=sen α
=cos α
=tg α
RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERARAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA

12. r=
1u.
r = 1 u.
r =
1
u.
α
α
α
α
r=1u.
cos α
senα
Cos α
Cos α
Senα
Cos α
Senα
senα
0º
90º = π/2 rad
180º = π rad
270º =3π /2 rad
360º = 2π rad
Signos del (coseno, seno)
en cada cuadrante
SIGNOS DE LAS RAZONES TRIGONOMÉTRICASSIGNOS DE LAS RAZONES TRIGONOMÉTRICAS
EN LOS DISTINTOS CUADRANTESEN LOS DISTINTOS CUADRANTES
(+,+)(- ,+)
(-,-) (+,-)
III
III IV

13. Si un ángulo mide α su suplementario mide 180º – α.
α
x
y
–x
180º – α
y
1
1
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS SUPLEMENTARIOSRAZONES TRIGONOMÉTRICAS DE ÁNGULOS SUPLEMENTARIOS
sen (180º – α) =
cos (180º – α) =
tan (180º – α) =
sen α
– cos α
– tan α

14. sen (180º + α) =
cos (180º + α) =
tan (180º + α) =
Si dos ángulos difieren en 180º y uno mide α el otro mide 180º + α.
α
x–x
180º + α
y
–y
1
1
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS QUE DIFIEREN EN 180ºRAZONES TRIGONOMÉTRICAS DE ÁNGULOS QUE DIFIEREN EN 180º
– sen α
– cos α
tan α

15. Sen (– α) = sen(360º – α) =
Cos (– α) = cos(360º – α) =
Si dos ángulos son opuestos y uno mide α el otro mide – α.
–y
y
α
x
–α
1
1
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS OPUESTOSRAZONES TRIGONOMÉTRICAS DE ÁNGULOS OPUESTOS
tan (– α) = tan (360º – α) =
– sen α
cos α
– tan α

16. Si un ángulo mide α su complementario mide 90º – α.
sen (90º – α) = AC / AB =
cos (90º – α) = BC / AB =
A
B
C
tan (90º – α) =
RAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOSRAZONES TRIGONOMÉTRICAS DE ÁNGULOS COMPLEMENTARIOS
α
90º - α
cos α
sen α
1 / tan α

17. 0º = 0 rad
r=1
cos 0º=1
sen 0º = 0
sen 0º= 0
cos 0º=1
tg 0º=
0
1
=0
cosc 0º=
1
0
=No existe
sec 0º=
1
1
=1
cotg 0º=
1
0
=No existe
RAZONES TRIGONOMÉTRICAS DE 0º = 0 radRAZONES TRIGONOMÉTRICAS DE 0º = 0 rad

18. 90º = rad
π
2
r=1
cos 90º = 0
sen 90º = 1
sen 90 º= 1
cos 90 º=0
tg 90 º=
1
0
=No existe
cosc 90 º=
1
1
=1
sec 90 º=
1
0
=No existe
cotg 90 º=
0
1
=0
RAZONES TRIGONOMÉTRICAS DERAZONES TRIGONOMÉTRICAS DE rad
2
π=90º

19. 180º = radπ
cos 180º=-1
sen 180º = 0
r=1
sen 180º=0
cos 180º=−1
tg 180º=
0
−1
=0
cosc 180 º=
1
0
=No existe
sec 180º=
1
−1
=−1
cotg 180º=
1
0
=No existe
RAZONES TRIGONOMÉTRICAS DERAZONES TRIGONOMÉTRICAS DE radπ=º180

20. 270º =
3π
2
rad
r=1
sen 270º =-1
cos 270º =0
sen 270º=−1
cos 270º=0
tg 270 º=
−1
0
=No existe
cosc 270º=
1
−1
=-1
sec 270º=
1
0
=No existe
cotg 270º=
0
−1
=0
RAZONES TRIGONOMÉTRICAS DERAZONES TRIGONOMÉTRICAS DE rad
2
π3=º270

21. BC
a
b c
A
90º
Fórmulas necesarias para resolver un triángulo rectángulo
•A + B + C = 180º ⇔ B + C = 90º
•Teorema de Pitágoras: a2
+ b2
= c2
Resolver un triángulo es calcular
todos los elementos del mismo
(lados y ángulos) a partir de
algunos de ellos.
b
a
senB =•
c
a
cosB =•
b
c
tanB =•
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOSRESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS

22. • Vamos a calcular el lado b.
RESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS. EJEMPLORESOLUCIÓN DE TRIÁNGULOS RECTÁNGULOS. EJEMPLO
• Vamos a calcular el lado c.
Podemos hacerlo por el teorema de
Pitágoras o por razones
trigonométricas. Hagámoslo de las dos
formas para comprobar que da el
mismo resultado.
PRIMERA FORMA: Teorema de Pitágoras.
SEGUNDA FORMA: Razones trigonométricas.

23. RESOLUCIÓN DE TRIÁNGULOS NO RECTÁNGULOS. EJEMPLORESOLUCIÓN DE TRIÁNGULOS NO RECTÁNGULOS. EJEMPLO
Pueden resolverse triángulos no rectángulos
aplicando correctamente las razones
trigonométricas. Veamos un ejemplo. Se
trata de calcular la altura h del triángulo de
color rosa.
Ahora debemos resolver el sistema de ecuaciones por igualación.
Consideramos el triángulo rectángulo
grande. Entonces:
Si consideramos el triángulo rectángulo
pequeño, entonces:
Por tanto:

24. FUNCIONES TRIGONOMÉTRICAS. FUNCIÓN SENOFUNCIONES TRIGONOMÉTRICAS. FUNCIÓN SENO
La función seno (sen x) asocia a cada valor de x el valor de sen x. La imagen
siguiente muestra inicialmente la función sen x. Se han puesto los valores de x
en radianes.
A cada ángulo podemos asociarle el valor de cada una de sus razones
trigonométricas. Se definen así las funciones trigonométricas.
Haz clic en el enlace y construye la función seno de forma interactiva.
FUNCIÓN SENO

25. La función coseno (cos x) asocia a cada valor de x el valor de cos x. La imagen
siguiente muestra inicialmente la función cos x. Se han puesto los valores de x
en radianes.
FUNCIONES TRIGONOMÉTRICAS. FUNCIÓN COSENOFUNCIONES TRIGONOMÉTRICAS. FUNCIÓN COSENO
Haz clic en el enlace y construye la función coseno de forma interactiva.
FUNCIÓN COSENO

26. FUNCIONES TRIGONOMÉTRICAS. FUNCIÓN TANGENTEFUNCIONES TRIGONOMÉTRICAS. FUNCIÓN TANGENTE
La función tangente (tg x) asocia a cada valor de x el valor de tg x. La imagen
siguiente muestra inicialmente la función tg x. Se han puesto los valores de x
en radianes.
Haz clic en el enlace y construye la función coseno de forma interactiva.
FUNCIÓN TANGENTE

27. HASTA PRONTO, CHAVALES.
ESPERO QUE HAYÁIS APRENDIDO MUCHO.
COMPROBAD VUESTRO APRENDIZAJE CON
LAS ACTIVIDADES QUE APARECEN EN LA
PÁGINA WEB.
¡¡¡¡ ADIOS !!!!