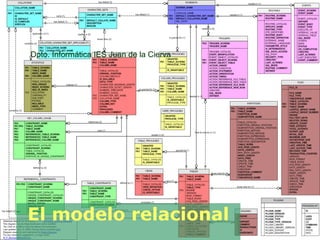
El documento describe los fundamentos del modelo relacional para bases de datos. Explica conceptos clave como tablas, relaciones, atributos, claves primarias y secundarias. Detalla las operaciones del álgebra relacional como selección, proyección, unión y diferencia de conjuntos. También cubre temas como lenguajes de consulta, valores nulos y modificación de datos.

1. El modelo relacional
Dpto. Informática IES Juan de la Cierva

2. Índice
1. Introducción
2. Tablas y relaciones
3. Claves
4. Lenguajes de consulta
5. Operaciones fundamentales del álgebra relacional
6. Otras operaciones del álgebra relacional
7. Valores nulos
8. Modificación de la BD
9. Bibliografía

3. Introducción
El modelo relacional es hoy en día el que más extensamente se
utiliza en aplicaciones comerciales.
Es simple, flexible y se adapta fácilmente a todo tipo de
requerimientos empresariales
Este modelo da lugar a productos de SGBD de tipo relacional, tanto
propietarios como GPL
Los fundamentos de este modelo son sólidos: los enunció Codd en
1970 utilizando un lenguaje matemático basado en la teoría de
conjuntos y las relaciones matemáticas
A lo largo de este tema, procederemos al estudio de dichos
fundamentos, así como a conocer toda la terminología asociada.

4. Tablas y relaciones
Una base de datos relacional consiste en una colección de tablas,
divididas en filas horizontales y columnas verticales, con un nombre
único.
Cada fila de la tabla representa una relación entre un conjunto de
valores (uno por columna)
Se denomina atributo a cada uno de los componentes de una fila de
una tabla. Son homogéneos en toda la tabla, esto es, toda la columna
tiene idéntico tamaño y el mismo domino
Se denomina dominio D de un atributo al conjunto de sus valores
posibles.
P. Ej, si un atributo es fecha_nacimiento, su dominio lo constituirían
todas las fechas válidas por sí mismas y/o en relación con una serie
de restricciones posibles
En terminología relacional, a las tablas se las denomina relacion, y a
las filas tupla

5. Tablas y relaciones
Por otra parte se denomina cardinalidad al número de tuplas que
tiene una tabla y grado al número de sus columnas

6. Tablas y relaciones (cont.)
Se exige, además, que para todas las relaciones los dominios de
todos los atributos sean atómicos, esto es, indivisibles
Por otra parte, es posible que varios atributos tengan el mismo
dominio, p. ej. el atributo fecha_nacimiento de un empleado y
fecha_ingreso en la empresa
Existe un valor especial que forma parte de todos los dominios, el
valor nulo, que indica desconocido o inexistente.
P. ej. si un empleado no tiene teléfono, el valor de este atributo sería
nulo.
No hay que confundir en atributos numéricos el valor nulo con
el 0, pues semántica y operacionalmente son cosas diferentes

7. Claves
Se denomina clave de una relación al atributo o grupo de atributos
que identifica de manera unívoca a una de sus tuplas, esto es, debe
tener un valor único diferenciado para cada una
Este es uno de los conceptos fundamentales que articulan el modelo
relacional, por lo que la identificación y elección de claves es crítica en
el modelo
Se denomina clave candidata a cualquier atributo o conjunto mínimo
de atributos que cumple el requisito anterior.
Si en una relación hay varias candidatas, habrá que decidir con cual
nos quedamos. La elegida pasará a denominarse clave primaria, o
simplemente clave
Suelen preferirse las claves cortas y a ser posible numéricas para
evitar problemas de identificación mayúsculas/minúsculas y que
además no cambien de valor casi nunca

8. Claves (cont.)
Si no existiera ninguna clave candidata, habría que añadir un
atributo que cumpliera esta función. Es la razón por la que “todos
somos un número”: como pacientes de la Seg. Social, como
clientes, empleados, etc.
En España, los individuos contamos con un DNI que nos identifica de
manera unívoca (se supone), pero aún así, la mayoría de las
administraciones prefieren establecer su propia codificación, ya que
suele implicar dígitos con otro significado, p. ej el número de
provincia, o de categoría profesional, etc.
Aparte de las claves primarias, existen otras de gran importancia:
las claves secundarias, externas o foreign keys que son atributos
que si bien no son claves en la tabla en la que están, si lo son en
otras tablas, y a través de ellas se ponen en relación los datos de
ambas

9. Claves (cont.)

10. Lenguajes de consulta
Un lenguaje de consultas es un lenguaje a través del cual los
usuarios solicitan información de la base de datos.
Suelen ser de nivel superior a los lenguajes de programación
habituales (4GL) y suelen clasificarse en:
•Procedimentales: hay que indicarle al sistema cómo
recuperar la información
•Declarativos: sólo hay que indicar lo que se quiere y no cómo
obtenerlo
El “lenguaje nativo” del modelo relacional, con fundamento
matemático como él, es el algebra relacional, que es de tipo
procedimental
El lenguaje de consulta de las bases de datos relacionales por
excelencia es SQL (Sample Query Language), declarativo, aunque
existen otras posibilidades como QBE (Query by Example) y Datalog

11. Operaciones fundamentales
del álgebra relacional
Estudiaremos en este apartado sólo las consultas a través del álgebra
relacional, aunque para que un LMD sea completo, es necesario que
incluya también posibilidad de modificación de datos
Las operaciones fundamentales son:
•Selección: extrae tuplas completas de una relación
•Proyección: extrae columnas completas de una relación
•Unión: obtiene la reunión de las tuplas de dos relaciones
•Diferencia de conjuntos: extrae las tuplas de una relación que
no están en otra relación
•Producto Cartesiano: obtiene una relación combinando las
tuplas de otras dos
•Renombramiento: da nombre al resultado de alguna de las
operaciones anteriores o combinaciones de ellas

12. Selección
Operación unaria.
Selecciona tuplas que satisfacen un determinado predicado. Osea,
extrae filas completas de una tabla.
Se representa con la letra griega sigma minúscula σ. El predicado
aparece como subíndice de σ

13. Proyección
Operación unaria
Selecciona una serie de atributos de una relación. Osea, extrae
columnas completas de una tabla.
Se representa con la letra griega pi mayúscula Π. La lista de
atributos a ser proyectada aparece como subíndice de Π

14. Unión
Operación binaria
La unión de dos relaciones con esquemas compatibles es otra
relación definida sobre el mismo esquema y formada por el
conjunto de tuplas de ambas eliminando las repeticiones.
Se representa con el operador típico de la teoría de conjuntos U
entre los nombres de las dos tablas a ser unidas

15. Diferencia de Conjuntos
Operación binaria
La operación diferencia de conjuntos, denotada por – permite obtener
las tuplas que están en una relación, pero no en la otra.
Como en el caso de la unión, ambas relaciones deben tener un
esquema compatible

16. Producto Cartesiano
Operación binaria
La operación producto cartesiano, denotada por x permite combinar
información de cualesquiera dos relaciones.
El resultado es una relación con tantas columnas como tienen las
dos relaciones sumadas, y nxm tuplas, siendo n y m el número de
tuplas de cada relación original

17. Renombramiento
Los resultados de las expresiones del álgebra relacional no tienen
un nombre que se pueda usar para referirse a ellas.
La operación renombramiento, denotada por la letra griega ro
minúscula ρ permite hacerlo:
ρNOMBRE(E)
La expresión entre paréntesis es la que recibe el renombramiento,
y puede ser:
•Una relación
•Una operación del álgebra relacional sobre una o más
relaciones
•Una composición de operaciones del álgebra relacional

18. Como esquema y resumen de las operaciones vistas, observemos
la siguiente imagen:
Selección

19. Otras operaciones del
álgebra relacional
Las operaciones fundamentales ya vistas son suficientes para poder
expresar cualquier consulta.
Sin embargo, algunas consultas habituales resultan complicadas de
expresar, por lo que se definen otras operaciones adicionales que si
bien no aumentan la potencia del álgebra relacional, si que
simplifican las consultas habituales.
Son, por ejemplo:
•Intersección de conjuntos
•Reunión natural
•División
•Asignación
•Proyección generalizada
•Funciones de agregación
•Reunión externa

20. Intersección de conjuntos
Operación binaria
La intersección ∩ de dos relaciones compatibles en su esquema, es
otra relación definida sobre el mismo esquema que contiene las
tuplas comunes a ambas

21. Reunión natural
Operación binaria
Combina el producto cartesiano de dos relaciones con una selección
de aquellas tuplas que satisfacen una condición específica.
Esta condición suele ser la igualdad en los valores de la clave
primaria de una relación que aparece como clave secundaria en la
otra.
Se denota con un símbolo parecido al aspa del producto cartesiano,
pero con dos trazos verticales en los extremos.

22. División
Operación binaria.
La división de una relación (dividendo) por otra (divisor) es una
relación cociente, tal que al realizarse su combinación con el
divisor, todas las tuplas resultantes se encuentran en el dividendo
Se denota por el símbolo operando de la división :

23. Asignación
En ocasiones resulta conveniente escribir una expresión del álgebra
relacional mediante la asignación de partes de esa expresión a
variables de relación temporal.
El operador asignación se denota por ← y se coloca a su izquierda la
variable relación temporal, y a la derecha la expresión relacional
La evaluación de una asignación no hace que se visualice ningún
resultado
P.ej:
Temp1 ← Пeditor ( AUTOR )

24. Proyección generalizada
Es una extensión de la proyección, permitiendo que se utilicen
funciones aritméticas en la lista de proyección.
Tiene el siguiente formato:
ΠF1,F2,..,Fn (E)
Donde E es cualquier expresión del álgebra relacional y F1,F2,…Fn
son expresiones aritméticas que incluyen constantes y atributos del
esquema E
Esto nos permite mostrar tanto valores de atributos tal y como
aparecen en la base, o transformados previamente a su
visualización.

25. Funciones de agregación
Toman un conjunto de valores y devuelve como resultado un único
valor.
Puede ser un recuento, media aritmética, suma, etc.
Normalmente se utilizan asociados a otro atributo por el cual se realiza
una agrupación previa, obteniéndose de esta forma una información de
tipo estadístico.
Trivialmente, se puede aplicar sobre toda la columna y se obtendría un
único valor resultado.

26. Reunión externa
Es similar a la reunión natural pero en el caso en que una tupla de
una tabla no tenga correspondencia en la otra, no desaparece del
resultado final, sino que aparece con los atributos que faltan
rellenos al valor nulo.
Dependiendo de cual es la tabla que aparece completamente
representada en el resultado final, se habla de:
•Reunión externa izquierda (outer left join)
•Reunión externa derecha (outer right join)
•Reunión externa simétrica (outer simetric join)

27. Valores nulos
Y Res
V D D
F D F
D D D
Vamos a definir a continuación la forma en que las diferentes
operaciones del álgebra relacional tratan a los valores nulos:
•Operaciones aritméticas: cualquier operación aritmética que
incluya un valor nulo, genera un resultado nulo
•Comparaciones: generan un resultado desconocido y por tanto
no verdadero
•Operadores lógicos: veamos sus tablas de verdad
O Res
V D V
F D D
D D D
NO Res
D D

28. Valores nulos (cont.)
•Selección: si la condición de selección devuelve el valor
verdadero, se añade la tupla al resultado, de lo contrario no
•Reunión: es un producto cartesiano seguido de una selección,
por lo que ocurre lo mismo que en el caso anterior
•Proyección: trata los valores nulos como a cualquier otro a la
hora de eliminar los valores duplicados
•Unión, intersección y diferencia: tratan de igual manera a los
valores nulos que el caso anterior
•Funciones de agregación: si hay valores nulos en los atributos
agrupados, se entienden como del mismo grupo. En los atributos
agregados, se desprecian antes de hacer los cálculos

29. Modificación de la BD
Hasta ahora hemos visto únicamente cómo se extrae información de
la base de datos, y a partir de ahora estudiaremos como se añaden,
eliminan y modifican sus datos
Borrado
Sólo se pueden borrar tuplas completas, y el resultado después del
borrado, no es mostrado al usuario.
En realidad el borrado se materializa como: r ← r – E
Dónde r es la relación de la que se eliminan las tuplas indicadas en E
Inserción
Se insertan también tuplas completas y al igual que antes, no se
visualiza nada.
La expresión correspondiente sería: r ← r U E

30. Modificación de la BD (cont.)
Actualización
Es la operación más compleja, pues en general es necesario primero
seleccionar la(s) tupla(s) y proyectar el(los) atributo(s) a modificar
La expresión para actualizar sería algo así:
r ← П A1,A2,..,An (σP( r )) U (r – σP( r ))
en la que se puede apreciar la proyección de una serie de atributos
Ai, que pueden ser los valores originales de cada uno o bien una
alteración de ellos vía una operación matemática o la sustitución de
su valor original por otro.
Esta proyección sólo se aplica a una selección previa de tuplas que
cumplen una condición P, y a continuación se produce la unión de
estas tuplas modificadas con las restantes de la relación original r

31. Bibliografía
Para ampliar información se recomienda consultar las siguientes
fuentes:
•Fundamentos de Bases de Datos.
Silberschatz, Korth, Sundarshan
Ed. McGraw-Hill
•Sistemas de Bases de Datos. Conceptos fundamentales
Elmasri, Navathe
Ed. Addison-Wesley
•Fundamentos y modelos de Bases de Datos
De Miguel, Piattini
Ed. RA-MA