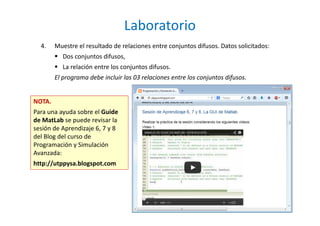
Este documento presenta los conceptos fundamentales de los conjuntos difusos y describe un laboratorio en MatLab sobre este tema. El objetivo del laboratorio es graficar funciones de pertenencia, calcular características de conjuntos difusos, realizar operaciones unarias y relaciones entre conjuntos. Se explican 8 funciones de pertenencia, 7 características de conjuntos difusos, 5 operaciones unarias y 3 relaciones entre conjuntos. El laboratorio guiará al usuario en la implementación de estos conceptos a través de una interfaz gráfica en MatLab.

1. M. Sc. Ing. José C. Benítez P.
Conjuntos Difusos
Laboratorio: 7
Inteligencia Artificial
(W0I9)

2. Objetivo
Fundamento teórico: Los conjuntos difusos.
Laboratorio: Los conjuntos difusos.
Informe de Laboratorio
Conjuntos Difusos
2

3. Objetivo
1. Revisar los conceptos de los conjuntos difusos.
2. Realizar interfaces graficas de usuario mediante el GUIDE de
MatLab.
3. Graficar mediante el MatLab las funciones de pertenencia.
4. Hallar las características de los conjuntos difusos mediante
MatLab .
5. Realizar las operaciones unarias de un conjunto difuso
mediante MatLab.
6. Calcular el resultado de las relaciones entre los conjuntos
difusos mediante MatLab.
7. Fortalecer su competencia redactora del alumno mediante
la redacción del informe de laboratorio con el desarrollo del
laboratorio.
3

4. Funciones de pertenencia
4
1. Triangular:
• Definido por sus límites inferior a y superior b, y el
valor modal m, tal que a < m < b.
• También puede representarse así:
A(x;a,m,b) = máx { mín{ (x-a)/(m-a), (b-x)/(b-m) }, 0 }

5. Funciones de pertenencia
5
2. Función Γ (gamma):
• Definida por su límite inferior a y el valor k>0.

6. Funciones de pertenencia
6
3. Función G (gamma):
– Se aproximan linealmente por:

7. Funciones de pertenencia
7
4. Función S:
• Definida por sus límites inferior a y superior b, y el
valor m, o punto de inflexión tal que a<m<b.
• Un valor típico es: m=(a+b) / 2.
• El crecimiento es más lento cuanto mayor sea la
distancia a-b.

8. Funciones de pertenencia
8
5. Función Gausiana:
• Definida por su valor medio m y el valor k>0.
• Es la típica campana de Gauss.
• Cuanto mayor es k, más estrecha es la campana.

9. Funciones de pertenencia
9
6. Función Trapezoidal:
• Definida por sus límites inferior a y superior d, y los límites
de su soporte, b y c, inferior y superior respectivamente.

10. Funciones de pertenencia
10
7. Función Pseudo-Exponencial:
• Definida por su valor medio m y el valor k>1.
• Cuanto mayor es el valor de k, el crecimiento es más
rápido aún y la “campana” es más estrecha.

11. Funciones de pertenencia
11
8. Función Trapecio Extendido:
• Definida por los cuatro valores de un trapecio [a, b, c, d], y
una lista de puntos entre a y b, o entre c y d, con su valor de
pertenencia asociado a cada uno de esos puntos.

12. Características de un conjunto difuso
12
1. Altura de un Conjunto Difuso (height):
El valor más grande de su función de pertenencia: supx∈X A(x).
2. Conjunto Difuso Normalizado (normal):
Si existe algún elemento x∈X, tal que pertenece al conjunto
difuso totalmente, es decir, con grado 1. O también, que:
Altura(A) = 1.
3. Soporte de un Conjunto Difuso (support):
Elementos de X que pertenecen a A con grado mayor a 0:
Soporte(A) = {x∈X | A(x) > 0}.
4. Núcleo de un Conjunto Difuso (core):
Elementos de X que pertenecen al conjunto con grado 1:
Nucleo(A) = {x∈X | A(x) = 1}.
Lógicamente, Nucleo(A) ⊆ Soporte(A).

13. Características de un conjunto difuso
13
5.α-Corte:
Valores de X con grado mínimo α: Aα = {x∈X | A(x) ≥ α}.
6. Conjunto Difuso Convexo o Concavo (convex, concave):
Si su función de pertenencia cumple que ∀x1 ,x2∈ X y ∀ λ∈[0,1]:
– Convexo: A(λx1+ (1–λ)x2) ≥ min{A(x1), A(x2)}.
Que cualquier punto entre x1 y x2 tenga un grado de
pertenencia mayor que el mínimo de x1 y x2
– Concavo: A(λx1+ (1–λ)x2) ≤ max{A(x1), A(x2)}.
7. Cardinalidad de un Conjunto Difuso con un Universo finito
(cardinality):
Card(A) = Σx∈X A(x).

14. Operaciones unarias en un conjunto difuso
14
1. Normalización:
Convierte un conj. difuso NO normalizado en uno
normalizado, dividiendo por su altura:
Norm_A(x) = A(x) / Altura(A)
2. Concentración (concentration):
Su función de pertenencia tomará valores más pequeños,
concentrándose en los valores mayores:
Con_A(x) = Ap(x), con p>1, (normalmente, p=2)
3. Dilatación (dilation):
Efecto contrario a la concentración. 2 formas:
Dil_A(x) = Ap(x), con p∈(0,1), (normalmente, p=0.5).
Dil_A(x) = 2A(x) – A2(x).

15. Operaciones unarias en un conjunto difuso
15
4. Intensificación del Contraste (contrast intensification): Se
disminuyen los valores menores a 1/2 y se aumentan los
mayores:
Con p>1. Normalmente p=2. Cuanto mayor p, mayor
intensificación.
5. Difuminación (fuzzification): Efecto contrario al anterior:

16. Relaciones entre conjuntos difusos
16
1. Igualdad (equality): Dos conjuntos difusos, definidos en el
mismo Universo, son iguales si tienen la misma función de
pertenencia: A = B ⇔ A(x) = B(x), ∀ x∈X
2. Inclusión (inclusion): Un conjunto difuso está incluido en
otro si su función de pertenencia toma valores más pequeños:
A ⊆ B ⇔ A(x) ≤ B(x), ∀ x∈X
3. Inclusión Difusa: Si el Universo es finito, podemos relajar la
condición anterior para medir el grado en el que un conjunto
difuso está incluido en otro (Kosko, 1992):

17. Laboratorio
17
Realizar un programa en Matlab mediante el Guide que:
1. Grafique cada una de las funciones de pertenencia. Datos solicitados:
La función de pertenencia,
Los valores de sus parámetros,
El universo del discurso.
El programa debe incluir las 08 funciones de pertenencia.
2. Muestre el resultado de una característica difusa elegida. Datos solicitados:
Un conjunto difuso,
La característica del conjunto.
El programa debe incluir las 07 características de los conjuntos difusos.
3. Muestre el resultado de una operación unaria elegida. Datos solicitados:
Un conjunto difuso,
La característica del conjunto.
El programa debe incluir las 05 operaciones unarias de los conjuntos difusos.

18. Laboratorio
18
4. Muestre el resultado de relaciones entre conjuntos difusos. Datos solicitados:
Dos conjuntos difusos,
La relación entre los conjuntos difusos.
El programa debe incluir las 03 relaciones entre los conjuntos difusos.
NOTA.
Para una ayuda sobre el Guide
de MatLab se puede revisar la
sesión de Aprendizaje 6, 7 y 8
del Blog del curso de
Programación y Simulación
Avanzada:
http://utppysa.blogspot.com

19. Informe de Laboratorio
Es un documento gráfico en lo posible y es redactado en Word con el
desarrollo de éste laboratorio.
Niveles de Informe:
Primer nivel: Observaciones y comentarios. Imágenes con
observaciones y comentarios cortos. Redactar al ir desarrollando el
laboratorio. (Requiere desarrollar el laboratorio).
Segundo nivel: Conclusiones. Redactar al terminar el
laboratorio.(Requiere haber desarrollado el laboratorio).
Tercer Nivel: Recomendaciones. (Requiere lectura de otras fuentes).
Presentación:
Dentro de su Carpeta Personal del Dropbox crear una carpeta para el
Laboratorio 7 con el siguiente nombre: IA_PaternoM_Lab7
Adjuntar en esta carpeta:
El Informe de Laboratorio 7.
Los archivos “*.fig” y “*.m” utilizados.
Las fuentes deben conservar el nombre original de archivo y se debe
agregar _L7 al final. 19

20. Laboratorio 7. Conjuntos difusos
Blog del curso:
utpiayse.blogspot.com
20