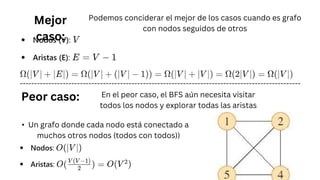
El documento discute la representación de grafos mediante listas de adyacencia y matrices de adyacencia, así como los algoritmos de búsqueda en grafos, específicamente la búsqueda en anchura (BFS). Se explica que el BFS es útil para encontrar la ruta más corta en grafos no ponderados y se analiza su complejidad, que es O(|v| + |e|). Se menciona que en el peor caso, se deben visitar todos los nodos y explorar todas las aristas.

3. •
•

4. Los grafos se pueden representar
utilizando diferentes métodos
computacionales, siendo los más
comunes las listas de adyacencia y
las matrices de adyacencia

5. Los algoritmos de búsqueda en
grafos, como la búsqueda en
anchura (BFS) y la búsqueda en
profundidad (DFS), son
fundamentales para explorar y
analizar la estructura de un grafo

6. Una lista de adyacencia de un grafo
G=(V,E) consiste en un array de∣V∣
listas. Para cada vértice u∈V, la lista
de adyacencia Adj[u] contiene
todos los vértices v tales que existe
una arista (u,v)∈E.

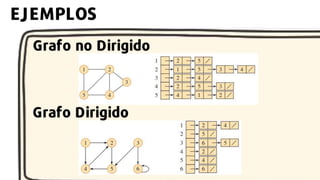
8. • Una matriz de adyacencia de un
grafo G=(V,E) es una matriz
∣V∣×∣V∣ A donde la entrada A[i][j]
es 1 si existe una arista (i,j)∈ E, y
0 en caso contrario.

11. Definicion
:
El algoritmo de búsqueda en anchura (Breadth-First Search o
BFS, por sus siglas en inglés) es un método ampliamente
utilizado en la teoría de grafos para explorar y buscar
vértices en un grafo de manera sistemática. Este algoritmo es
particularmente útil en grafos no ponderados y se destaca
por su capacidad para encontrar la ruta más corta desde un
nodo origen a un nodo destino, siempre y cuando todos los
bordes tengan el mismo peso

12. Ejemplo:
Cola:
Recorrido
:

13. Codigo:

14. Codigo:

15. Analizando la Complejidad:
𝑂(∣𝑉∣)+𝑂( 2∣𝐸∣)= 𝑂(∣𝑉+𝐸∣)
Dado que:
• Cada nodo se visita una vez: 𝑂(∣𝑉∣)
• Cada arista se explora dos veces: 𝑂(2∣𝐸∣), que es
simplificado a 𝑂(∣𝐸∣)

16. Mejor
caso:
Peor caso: En el peor caso, el BFS aún necesita visitar
todos los nodos y explorar todas las aristas
• Un grafo donde cada nodo está conectado a
muchos otros nodos (todos con todos))
Podemos conciderar el mejor de los casos cuando es grafo
con nodos seguidos de otros
--------------------------------------------------------------------------------------------------

17. Complejidad Asintótica del BFS