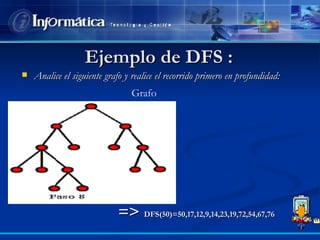
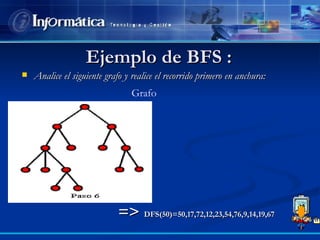
Este documento describe dos técnicas para recorrer un grafo: recorrido en profundidad (DFS) y recorrido en anchura (BFS). El DFS busca los caminos más largos primero mientras que el BFS visita los nodos por niveles de distancia desde el nodo inicial. Se proveen ejemplos y pseudocódigo para implementar DFS y BFS usando una cola y marcando vértices visitados.

1. ESTRUCTURA DE DATOS II RECORRIDOS DE GRAFOS UNIVERSIDAD AUTONOMA GABRIEL RENE MORENO FACULTAD DE CIENCIAS EXACTAS Y TECNOLOGIA PROFESOR: Ing. Evans Balcazar Veizaga

2. Recorridos en Grafos: Recorrer un grafo significa tratar de alcanzar todos los nodos que estén relacionados con uno que llamaremos nodo de salida. Existen básicamente dos técnicas para recorrer un grafo: el recorrido en anchura y el recorrido en profundidad. Así, para recorrer un grafo consiste en visitar todos los vértices alcanzables a partir de uno dado. Hay dos formas. Recorrido en profundidad (DFS). Recorrido en anchura (BFS).

3. Recorrido en Profundidad (DFS) : Trata de buscar los caminos que parten desde el nodo de salida hasta que ya no es posible avanzar más. Cuando ya no puede avanzarse más sobre el camino elegido, se vuelve atrás en busca de caminos alternativos, que no se estudiaron previamente. La búsqueda en profundidad empieza por un vértice V. del grafo G; V no visitado; así hasta que no haya mas vértices adyacentes no visitados.

4. Ejemplo de DFS : Analice el siguiente grafo y realice el recorrido primero en profundidad: Grafo => DFS(50)=50,17,12,9,14,23,19,72,54,67,76

5. Recorrido en Anchura (BFS) : Supone recorrer el grafo, a partir de un nodo dado, en niveles, es decir, primero los que están a una distancia de un arco del nodo de salida, después los que están a dos arcos de distancia, y así sucesivamente hasta alcanzar todos los nodos a los que se pudiese llegar desde el nodo salida. Este método comienza visitando el vértice de partida A, para continuación visitar los adyacentes que no estuvieron ya visitados. Así sucesivamente con los adyacentes. Este método utiliza una cola como estructura auxiliar en la que se mantienen los vértices que se vayan a procesar posteriormente.

6. Ejemplo de BFS : Analice el siguiente grafo y realice el recorrido primero en anchura: Grafo => DFS(50)=50,17,72,12,23,54,76,9,14,19,67

7. Implementación de DFS : Se utilizara una composición de la class conjunto, para llevar la cuenta de los vértices marcados: void DFS(int v) { Conjunto v; DFS(v,c); } void DFS(int v1,Conjunto c) { cout<<v1; c.insertar(v1); for( w.adyancente(v1)) if(!c.pertenece(w)) DFS(w,c); } void DFS(int v1,Conjunto c) { cout<<v1; puntero L=V[v1]; while( L!=Tierra) { int w=Data(L); if(!c.pertenece(w)) DFS(w,c); } }

8. Implementación de BFS : Se utilizara una composición de la class conjunto, para llevar la cuenta de los vértices marcados: void grafo:: DFS(int v) { Conjunto v; Cola q; q.meter(v); do{ int w; q.sacar(w); if(!c.pertenece(w))//no marc { cout<<w; q.insertar(w);//marc for(x.adyacente(w)) { if(!c.pertecene(x)) q.meter(x); } } } while(!q.vacia()) }

9. ¿Ahora a Trabajar?

10. GRACIAS INF-310 Estructura de Datos II