Continuidad derivada sppt
•Descargar como PPT, PDF•
1 recomendación•2,189 vistas
PPT de derivadas nivel básico
Denunciar
Compartir
Denunciar
Compartir
Más contenido relacionado
La actualidad más candente
La actualidad más candente (20)
Destacado
Concepto geométrico de la derivada de una función y su relación con la recta ...

Concepto geométrico de la derivada de una función y su relación con la recta ...Fernando Felix Solis Cortes
Destacado (8)
Concepto geométrico de la derivada de una función y su relación con la recta ...

Concepto geométrico de la derivada de una función y su relación con la recta ...
Similar a Continuidad derivada sppt
Similar a Continuidad derivada sppt (20)
Último
Último (10)
POWER POINT YUCRAElabore una PRESENTACIÓN CORTA sobre el video película: La C...

POWER POINT YUCRAElabore una PRESENTACIÓN CORTA sobre el video película: La C...
Presentación guía sencilla en Microsoft Excel.pptx

Presentación guía sencilla en Microsoft Excel.pptx
Global Azure Lima 2024 - Integración de Datos con Microsoft Fabric

Global Azure Lima 2024 - Integración de Datos con Microsoft Fabric
Proyecto integrador. Las TIC en la sociedad S4.pptx

Proyecto integrador. Las TIC en la sociedad S4.pptx
Continuidad derivada sppt
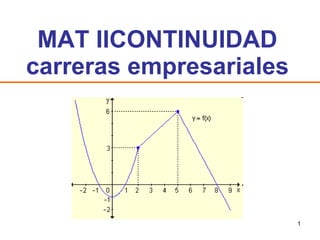
- 1. MAT IICONTINUIDAD carreras empresariales
- 6. 6 5
- 7. Discontinuidad Remediable o Reparable o eliminable EJEMPLO Analizar el tipo de discontinuidad en el punto dado 1 2
- 8. NIVEL REPRODUCTIVO TALLER 8 = DEBER 8 1 2 3
- 10. 6
- 11. NIVEL CRITICO 7 8 Determinar A y B de modo que f sea continua en R
- 16. Una constante por la función [3] Siendo k un número real Ejemplo: derivar Una constante pura [4] Donde k representa una constante Ejemplo: derivar a) b)
- 21. REGLA DE LA CADENA EJEMPLO Hallar la derivada de f(g(x))
- 22. [13] Siendo n un número real distinto de 0 función como base [14] función como ángulo Ejemplo: derivar Ejemplo: derivar
- 30. NIVEL CRITICO
- 31. EJEMPLOS TEOREMA 1 2 Demostración:…….
- 32. GUIA DE REFUERZO
- 33. GUIA DE REFUERZO
- 34. EJEMPLO DE UNA FUNCIÓN NO DERIVABLE
- 35. DERIVADA EN UN PUNTO SITUACIONES
- 36. INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA
- 37. TALLER 10 = DEBER 10
- 39. EJEMPLOS
- 40. TALLER 11 = DEBER 11
