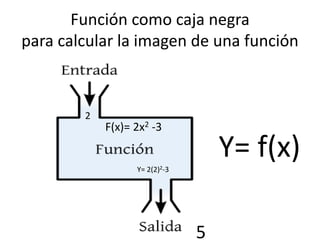
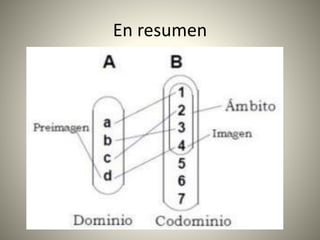
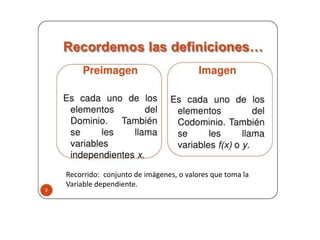
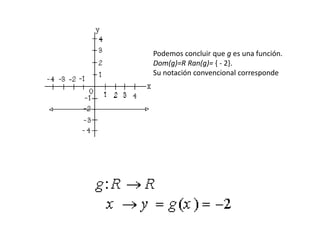
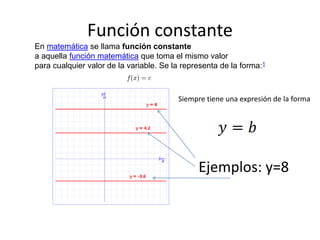
El documento aborda conceptos fundamentales de matemáticas, en particular funciones y sus propiedades, como dominio, recorrido, imágenes y preimágenes. Se presentan ejemplos de cómo calcular el dominio y rango de diversas funciones, así como la importancia de la representación gráfica en la identificación de funciones. Además, se discute el concepto de funciones constantes y afines, así como su comportamiento y características en relación con el gráfico.

1. funciones
Aprender bien es mi meta

2. funciones
Aprender bien es mi meta.
RELACIÓN DE DEPENDENCIA, entre dos variables,
en la que a cada valor de la Variable independiente,
le corresponde un único valor de la variable independiente.

3. EJEMPLOS
2

4. 2

5. función

6. Función o no función

7. Un ejemplo de la realidad
Ejemplo: este árbol crece 20 cm cada año,
así que la altura del árbol está relacionada con la edad
por la función x: F(x) = 20 x
¿Cuáles son los valores posible de las preimágenes?
Lo que puede entrar en una función se llama el
dominio.

8. Función como caja negra
para calcular la imagen de una función
F(x)= 2x2 -3
2
Y= 2(2)2-3
5
Y= f(x)

9. Cálculo de la preimagen
• F(x)= 2x2 -3
• Cual es la pre imagen de 5?
• 5= 2x2 -3
• Hacemos los cálculos.
• - 2x2 = -3-5
• - 2x2 = -8
• 2x2 = 8
• x2 =
• X=

10. Practiquemos
• En la función F(x)= 3x2-2
• La imagen 10, que número contiene como
preimagen.
• Cual es la imagen de 3.
• Realice el gráfico de la función. Econtrando las
imágenes para -3, -2, 0 , 2 y 3.

12. Autoevaluación:
Resolver el sistema
En la ecuación 1 obtenga las imágenes de -4 y -3
En la ecuación 2, obtenga las imágenes de -4 y 2
Comparar la Solución

13. En la (1): 2y= -5-3x
Tabla
De valores
Graficar los puntos y trazar la recta de la ecuación 1

14. En la (2): 5y=4-2x
y
Tabla
De valores

16. Concepto de Dominio
• Se llama dominio de definición de
una función f, y se designa Dom f, al
conjunto de valores de la variable
independiente x para los que existe
la función, es decir, para los que hay
un valor de la variable dependiente
y.

17. Concepto de recorrido
Se llama recorrido de una función, y
se designa Rec f, a todos los valores
de la variable dependiente que tienen
algún valor de la variable
independiente que se transforma en
él por la función.

18. Ejemplo gráfico

19. Función como caja negra
para calcular la imagen de una
función
F(x)= 2x2 -3
2
Y= 2(2)2-3
5
Y= f(x)
Lo que puede entrar en una función se
llama el dominio
Lo que es posible que salga de una función
se llama el codominio
Imagen o rango
preimagen

20. Ejemplo 1
Si A = {1, 2, 3} y B = {2, 4, 6} y su
correspondencia es el doble.
Entonces f(x) = 2x
En efecto
f(1) = 2 • 1 = 2
f(2) = 2 • 2 = 4
f(3) = 2 • 3 = 6
Tenemos
Dominio = {1, 2, 3}
Codominio = {2, 4, 6}
Ámbito (rango o recorrido) = {2, 4, 6}

21. Ejemplo 2
Si A = {1, 3, 5} y B = {3, 5, 7, 9, 11}
y su correspondencia es el doble más uno.
Entonces f(x) = 2x + 1
En efecto:
f(1) = 2 • 1 + 1 = 3
f(3) = 2 • 3 + 1 = 7
f(5) = 2 • 5 + 1 = 11
Tenemos
Dominio = {1, 3, 5}
Codominio = {3, 5, 7, 9, 11}
Ámbito (rango o recorrido) = {3, 7, 11}

22. En resumen

23. Recorrido: conjunto de imágenes, o valores que toma la
Variable dependiente.

24. Si tenemos f(x)= 3x + 5 ¿Cuál es la
preimagen de 11?
• Sea f(x)= X2 – 6x + 7 ¿Cuál es la imagen de 7?
• Para elaborar empanadas una señora gasta $ 30 por
cada empanada que hace además de $ 750 por día
en gastos fijos.
• A. ¿Cuánto gastará elaborando 25 empanadas?
• B. ¿Cuánto gastará elaborando 50 empanadas?
• 4. En una fábrica gastan $ 1.275 por cada par de
zapatos elaborado y tiene un gasto de $ 13.500 por
día. ¿Cuanto gastan en la elaboración de 350 pares
de zapatos?

25. Características de las funciones

26. Determinar cuáles de las relaciones dadas son
funciones, aplicando el criterio gráfico. Especificar para
cada una, dominio y rango.
• Podemos concluir que f es una función.
Dom(f)=R Ran(f)=R .
• Expresemos su notación convencional:

27. Podemos concluir que g es una función.
Dom(g)=R Ran(g)= { - 2}.
Su notación convencional corresponde

28. Podemos concluir que la relación k no es una función. Dom(k)= [0, ) Ran(k)=R .

29. Una prueba de la recta vertical se utiliza para determinar si una relación trazada en un
gráfico es una función o no. Para hacer la recta vertical prueba, represente la relación
gráficamente, y después mire el gráfico. Si dondequiera usted puede colocar una recta
vertical pasa a través del gráfico a lo más una vez, después la relación es una función. Si
cualquier recta vertical pasa a través del gráfico más de una vez, la relación no es una
función

31. Deber
1. En hojas de papel milimetrado resolver el sistema:
3. Realizar en la misma hoja el grafico de la función: y = x2
4.Racionalizar:
5- Sea f(x)= 2x2 + 7. Hallar la preimagen para cuando: f(x) = 57
6. Sea f(x)= x2 +2 construya la gráfica con la preimagenes:
7. La gráfcia de F(x) = 3x2 + 2x -1 las preimágenes: -5…….0…….5
2. ¿Qué vehículo va más rápido el que transita a 7 m/s o el que lo hace 50 Km/h.

33. 2. ¿Qué vehículo va más rápido el que transita a 7 m/s o el que lo hace 50 Km/h.
7
= 25,2 Km/h Va más rápido 50Km/h.7
50 = 13,88 Km/H
cóncava hacia arriba

35. f(x)= 2x2 + 7
57= 2x2 + 7
-2x2=-57 +7
-2x2=-50
2x2=50
X2=
X=
X=5

36. relación función función
Función
función
Realizar la gráfica de F(x)= x3-9x.

37. (6,10)
(12,0)
(0,0)
origen
Raíz de la función

38. INTERSECCIÓN CON LOS EJES
Puntos de corte en OX
(1,0)
(4,0)
(8,0)

39. Crecimiento y decrecimiento
Decrece la función: no sube o se mueve
Izquierda arriba a derecha abajo [11, 14]
Crece la función: No baja o se mueve
De izquierda abajo a derecha arriba [0,3]
Crece:
0
3
Estrictamente creciente
14 16
-2 11

40. decreciente

41. Estrictamente creciente
-3 4
[-3, 4)

42. Estrictamente decreciente
-5 4
[-5, 4]

43. Espacio= velocidad por tiempo
V= 80km/h
Tiempo esta en la gráfica
Estrictamente Creciente
espacio

44. Crecimiento y decrecimiento
La función g(x) = -x3 es una función
decreciente en los números reales
La función f(x) = x2 es una función decreciente
en el intervalo de menos infinito a cero y
creciente en el intervalo de cero a infinito.
La función identidad es la función de la forma
f(x) = x. El dominio y el recorrido es el
conjunto de los números reales

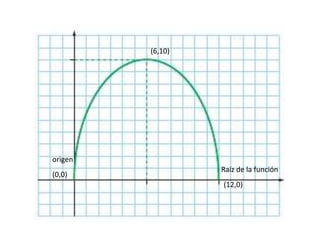
45. Monotonía a trozos
[0,6] creciente [6,12] decreciente
Creciente y decreciente en un mismo gráfico

46. Continuidad de una función
Generalmente una función continua es aquella cuya gráfica
puede dibujarse sin levantar el lápiz del papel

47. Función constante
En matemática se llama función constante
a aquella función matemática que toma el mismo valor
para cualquier valor de la variable. Se la representa de la forma:1
Siempre tiene una expresión de la forma
Ejemplos: y=8

48. Ordena en el origen
ORDENADA EN EL
ORIGEN.
3,6
8

49. Obtención de la expresión algebraica
de una función constante
Ecuación o expresión
algebraica:
Dominio:
Recorrido
Ecuación o expresión
algebraica:
Dominio:
Recorrido

50. DEBEREscriba los resultados de los siguientes productos notables:
(x + 5)2=
(2x - 5)2=
(2x + 4y )3=
Realice las siguientes multiplicaciones:
Realice la división:
Expresa en forma de radical:
RACIONALIZAR
Resuelva el sistema:
por el método de sustitución.
Resuelva el sistema:
por el método GRÁFICO.
Convertir 90 Km/h a m/s Escribir en notación científica: 0,00023 y 35400000

51. Funciones afines
m<0
m>0
m=

52. Funciones afines

53. Ley de formación: Y=mx +b
Pendiente de la recta
Ordenada en el origen
Que pasa si m = 0?
b

54. Dominio :
recorrido
Es creciente desde: [0, + [
Es decreciente desde: ]- , 0]

55. Graficar una recta:
(sin tabla)Para graficar una recta se deben tener en cuenta la
pendiente de la misma y la ordenada al origen. Grafiquemos la
recta:
y= 3 x+ 1
La ordenada al origen es (0, 1), el o primero que ubicamos en
el gráfico. A partir de ese punto aplicamos el concepto de
pendiente, subimos tres (por que el valor es positivo, sentido
positivo del eje y; de ser negativo bajaríamos) y corremos uno
hacia la derecha (sentido positivo del eje de las x). Por esos
dos puntos trazamos la recta.

56. Función lineal o de proporcionalidad
directa.
El número de albañiles y el tiempo empleado en construir un mismo edificio.
La velocidad de un vehículo y el espacio recorrido en el mismo tiempo.
x 18 9 6
y 3 4

57. Función lineal o de proporcionalidad
Inversa.
2. Las magnitudes
x e y de la tabla siguiente son inversamente proporcionales:
a) ¿Cuál es su constante de proporcionalidad?
b) ¿Qué relación funcional presentan?(Cuál es la ecuación?)
c) Completa los valores que faltan en la tabla.x
x 18 9 6
y 3 4

60. Función exponencial

61. Función exponencial