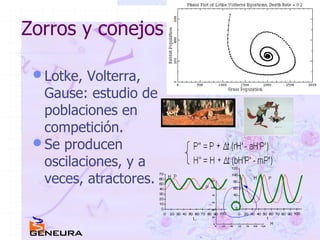
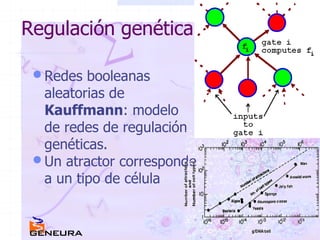
El documento explora la intersección entre matemáticas y biología, empezando con la secuencia de Fibonacci en la reproducción de conejos y avanzando hacia conceptos como catástrofes y morfología. Discute modelos matemáticos de dinámica poblacional y crecimiento biológico, incluyendo la teoría de redes de regulación genética y extinciones en ecosistemas. Además, se analizan estudios sobre correlación y herencia, así como modelos individuales en simulaciones biológicas.

1. J.J. Merelo Guervós Modelos matemáticos en Biología

2. Matemáticas y Biología

3. La historia empieza...

4. Leonardo Pisano, (a) Fibonacci Se ponen un par de conejos en un campo rodeado de vallas. ¿Cuántos conejos se pueden producir en un año?: 1, 1, 2, 3, 5, 8, 13, 21

5. Crecimiento y forma D´Arcy Thompson afirma que las formas vivientes no están más allá de una descripción matemática. Las formas vivientes obedecen las mismas leyes de física y química que las inanimadas.

6. Catástrofes René Thom, propone la teoría de catástrofes y el “campo morfogenético” para describir transiciones de fase, especialmente en etología y ecología.

7. Manchas y conchas Turing intenta explicar mediante ecuaciones en derivadas parciales la creación de distribuciones no-homogéneas. Propone la ecuación de reacción difusión:

8. Crecimiento de las plantas Los esquemas de crecimiento están dominados genéticamente, y son esquemas de desarrollo, no acretivos: L-sistemas.

9. Naturaleza fractal Mandelbrot describe objetos con una geometría patológica, y una sorprendente similitud a objetos naturales.

10. Sistemas de funciones iteradas Julia y Fatou estudiaron, usando las familias normales de Montel, los sistemas de funciones iteradas.

11. Atractores de Lorenz Descubrió desdoblamiento de períodos en la función logística: rx(1-x). Atractor de Lorenz: demuestra sensibilidad a las condiciones iniciales

12. Zorros y conejos Lotke, Volterra, Gause: estudio de poblaciones en competición. Se producen oscilaciones, y a veces, atractores.

13. Moscas en la miel Axtell/Epstein , Holland , y otros, proponen los modelos basados en individuo o modelos tácticos para simulación en Biología. Los modelos incorporan dentro de cada agente detalles relevantes para lo que se quiere probar. Biología, Ecología, Diversidad

14. Altos y bajos Galton estudió la correlación entre la estatura de cada generación. Media condicionada Estadísticos y biométricos se opusieron al mendelismo El análisis factorial reconcilia la herencia discreta con las leyes probabilísticas.

15. Regulación genética Redes booleanas aleatorias de Kauffmann : modelo de redes de regulación genéticas. Un atractor corresponde a un tipo de célula

16. ¿Mala suerte o malos genes? Per Bak aplica las RAB y la criticalidad auto-organizada a modelos de extinción. Predice tamaños y frecuencias de extinción similares a la realidad. Extinciones provocadas por “avalanchas coevolutivas”

17. Extinciones Fin