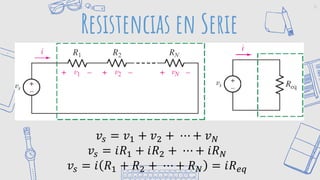
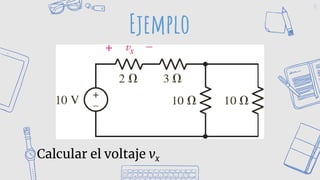
Este documento presenta conceptos básicos sobre circuitos eléctricos, incluyendo leyes de Kirchhoff, nodos, trayectorias, mallas, resistencias en serie y paralelo, y divisores de voltaje y corriente. Explica cómo usar estas herramientas para determinar voltajes, corrientes y potencias en circuitos.