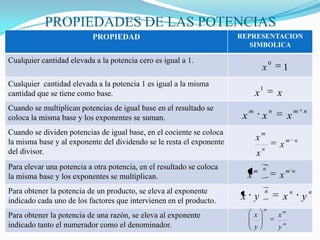
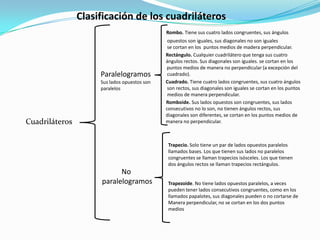
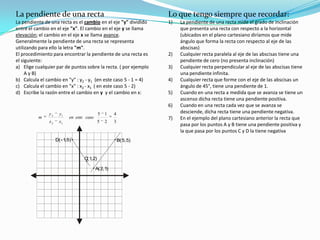
El documento presenta información sobre conceptos matemáticos como las leyes de los signos, propiedades de potencias, productos notables, clasificación de triángulos y cuadriláteros, el teorema del binomio de Newton y conceptos sobre la pendiente de una recta.

1. ACORDEON DE MATEMATICAS NOMBRE DEL ALUMNO ESCUELA,GRADO Y GRUPO NOMBRE DEL MAESTRO, ETC.

3. PROPIEDADES DE LAS POTENCIAS

4. OTRAS PROPIEDADES DE LAS POTENCIAS

5. PRODUCTOS NOTABLES BINOMIO AL CUBO Para elevar un binomio al cubo se hace lo siguiente: Se eleve al cubo el primer término del binomio. Se obtiene el triple de la multiplicación del cuadrado del primer término por el segundo. Se obtiene el triple de la multiplicación del primer término por el cuadrado del segundo. Se eleva al cubo el segundo término del binomio. Cuando el signo de b es negativo, los signos del resultado quedan alternados, comenzando con positivo: BINOMIO AL CUADRADO Al resultado de elevar un binomio al cuadrado se le llama un trinomio cuadrado perfecto(TCP) y para obtenerlo se hace lo siguiente: Se eleva al cuadrado el primer término del binomio Se obtiene el doble del producto del primer término por el segundo Se eleva al cuadrado el segundo término del binomio PRODUCTO DE BINOMIOS CONJUGADOS Al resultado de multiplicar dos binomios conjugados se le llama una diferencia de cuadrados y para obtenerla se hace los siguiente: Se eleva al cuadrado el término común Se obtiene el producto de los términos simétricos TRINOMIO AL CUADRADO PRODUCTO DE BINOMIOS CON TERMINO COMUN Cuando se multiplican dos binomios que tienen un término común, dan como producto un binomio de segundo grado, para obtenerlo se hace lo siguiente: Se eleva al cuadrado el término común Se suman los términos no comunes y el resultado se multiplica por el término común Se obtiene el producto de los términos no comunes JERARQUIZACION DE LAS OPERERACIONES PRIMERO. Potencias y raíces. SEGUNDO. Multiplicaciones y divisiones. TERCERO. Sumas y restas Cuando hay paréntesis, se resuelve primero lo que está contenido en ellos.

6. Clasificación de los triángulos ÁNGULOS QUE SE FORMAN CUANDO DOS PARALELAS SON CORTADAS POR UNA SECANTE O TRANSVERSAL 1. Clasificación de triángulos según la medida de sus lados Triángulo Equilátero Es aquel que tiene todos sus lados de la misma medida, en donde: 2 1 R1 3 4 5 6 Triángulo Isósceles Es aquel que tiene sólo dos lados de igual medida. R2 7 8 Colaterales internos: Están del mismo lado de la secante, en la región interior, en distinta recta y son suplementarios (3 y 5, 4 y 6) Colaterales externos: Están del mismo lado de la secante, en la región exterior, en distinta recta y son suplementarios (1 y 7, 2 y 8) Alternos internos: Están en distinto lado de la secante, en la región interior, en diferente recta y son iguales (3 y6, 4 y 5) Alternos externos: Están en distinto lado de la secante, en la región exterior, en diferente recta y son iguales (1 y 8, 2 y 7) Correspondientes: Uno es interno y el otro externo, están del mismo lado de la secante, en distinta recta y son iguales (1 y 5, 3 y 7, 2 y 6, 4 y 8) Opuestos por el vértice: Uno es interno y el otro externo, están en distinto lado de la secante, en la misma recta y son iguales (1 y 4, 2 y 3, 5 y 8, 6 y 7) Triángulo Escaleno Es aquel que tiene todos sus lados de distinta medida. 2. Clasificación de triángulos según la medida de sus ángulos Triángulo Acutángulo Aquel que tiene todos sus ángulos agudos. Triángulo Rectángulo Aquel que tiene un ángulo recto (< CAB). Triángulo Obtusángulo Aquel que tiene un ángulo obtuso, tal como se muestra a continuación:

7. Clasificación de los cuadriláteros Rombo. Tiene sus cuatro lados congruentes, sus ángulos opuestos son iguales, sus diagonales no son iguales se cortan en los puntos medios de madera perpendicular. Rectángulo. Cualquier cuadrilátero que tenga sus cuatro ángulos rectos. Sus diagonales son iguales. se cortan en los puntos medios de manera no perpendicular (a excepción del cuadrado). Cuadrado. Tiene cuatro lados congruentes, sus cuatro ángulos son rectos, sus diagonales son iguales se cortan en los puntos medios de manera perpendicular. Romboide. Sus lados opuestos son congruentes, sus lados consecutivos no lo son, no tienen ángulos rectos, sus diagonales son diferentes, se cortan en los puntos medios de manera no perpendicular. Paralelogramos Sus lados opuestos son paralelos Cuadriláteros Trapecio. Solo tiene un par de lados opuestos paralelos llamados bases. Los que tienen sus lados no paralelos congruentes se llaman trapecios isósceles. Los que tienen dos ángulos rectos se llaman trapecios rectángulos. Trapezoide. No tiene lados opuestos paralelos, a veces pueden tener lados consecutivos congruentes, como en los llamados papalotes, sus diagonales pueden o no cortarse de Manera perpendicular, no se cortan en los dos puntos medios No paralelogramos

8. El binomio de Newton (teorema del binomio) OBSERVACIONES: f) El coeficiente del segundo término del desarrollo siempre coincide con el exponente al que está elevado el binomio. g) El coeficiente del tercer término se obtiene multiplicando el coeficiente del segundo término por el exponente de a en ese mismo término y dividir el resultado entre el exponente de b aumentado en uno. El coeficiente del cuarto término se obtiene multiplicando el coeficiente del tercer término por el exponente de a en ese mismo término y dividir el resultado entre el exponente de b aumentado en uno. Se repite el proceso hasta obtener el coeficiente del último término. También se puede notar que hay simetría en la distribución de los coeficientes en el desarrollo. Si en cada termino se suman los exponentes de a y b, siempre se obtiene como resultado el mismo número que tiene de exponente el binomio. Los coeficientes del desarrollo se ajustan al triángulo de Pascal. DESARROLLOS: (a+b)0 = 1 (a+b)1 = a + b (a+b)2= a2+2ab+b2 (a+b)3= a3+3a2b+3ab2+b3 (a+b)4=a4+4a3b+6a2b2+4ab3+b4 (a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 (a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b4+6ab5+b6 (a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7 (a-b)7=a7-7a6b+21a5b2-35a4b3+35a3b4-21a2b5+7ab6-b7 OBSERVACIONES: En los desarrollos anteriores podemos notar que: El número de términos del desarrollo siempre es el exponente del binomio aumentado en uno. El primer término del desarrollo siempre es la a elevada al mismo exponente que presenta el binomio. Los exponentes de a van disminuyendo de uno en uno en los términos subsiguientes, hasta que desaparece a en el ultimo término. El primer término no contiene b, esta aparece por primera vez en el segundo término elevada a la potencia 1 y de ahí va aumentando de uno en uno en los términos subsiguientes. El último término del desarrollo es b elevada al mismo exponente que tiene el binomio.

9. Lo que tengo siempre que recordar: La pendiente de una recta mide el grado de inclinación que presenta una recta con respecto a la horizontal (ubicados en el plano cartesiano diríamos que mide ángulo que forma la recta con respecto al eje de las abscisas) Cualquier recta paralela al eje de las abscisas tiene una pendiente de cero (no presenta inclinación) Cualquier recta perpendicular al eje de las abscisas tiene una pendiente infinita. Cualquier recta que forme con el eje de las abscisas un ángulo de 45°, tiene una pendiente de 1. Cuando en una recta a medida que se avanza se tiene un ascenso dicha recta tiene una pendiente positiva. Cuando en una recta cada vez que se avanza se desciende, dicha recta tiene una pendiente negativa. En el ejemplo del plano cartesiano anterior la recta que pasa por los puntos A y B tiene una pendiente positiva y la que pasa por los puntos C y D la tiene negativa La pendiente de una recta La pendiente de una recta es el cambio en el eje "y" dividido entre el cambio en el eje "x". El cambio en el eje y se llama elevación; el cambio en el eje x se llama avance. Generalmente la pendiente de una recta se representa utilizando para ello la letra "m". El procedimiento para encontrar la pendiente de una recta es el siguiente: Elige cualquier par de puntos sobre la recta. ( por ejemplo A y B) Calcula el cambio en "y" : y2 - y1 (en este caso 5 - 1 = 4) Calcula el cambio en "x" : x2 - x1 ( en este caso 5 - 2) Escribe la razón entre el cambio en y y el cambio en x: