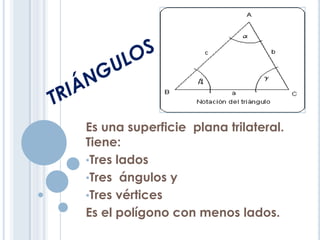
Este documento proporciona una descripción detallada de los triángulos. Define un triángulo como una figura plana de tres lados y tres ángulos. Clasifica los triángulos según la igualdad de sus lados y ángulos, y describe las rectas y puntos notables como medianas, mediatrices, bisectrices y alturas. También cubre la congruencia de triángulos y algunos teoremas importantes sobre la suma de ángulos.

1. Es una superficie plana trilateral.
Tiene:
•Tres lados
•Tres ángulos y
•Tres vértices
Es el polígono con menos lados.

2.  Para designar un triángulo se
emplea el símbolo y para el
plural s .
 Para nombrarlo se pueden usar las
3 letras de sus vértices en cualquier
orden.

3. CLASIFICACIÓN DE TRIÁNGULOS
 Seclasifican según la igualdad o la
desigualdad de sus lados , o la
clase de ángulos que tengan:

4. CLASIFICACION DE LOS TRIÁNGULOS
SEGÚN SUS LADOS
a) TRIÁNGULO ESCALENO: es aquel
que ninguno de sus lados son
iguales.

5. b) TRIÁNGULO
ISOSCELES: tiene
iguales dos de sus
lados.

6. c) TRIÁNGULO EQUILATERO: tiene sus tres
lados iguales; también se le llama
acutángulo, por tener sus tres lados
iguales (estos miden siempre 60°).

7. CLASIFICACION DE LOS TRIÁNGULOS
SEGÚN SUS ÁNGULOS.
a) TRIÁNGULO RECTÁNGULO: tiene
un ángulo recto (90°).

8. b) TRIANGULO OBTUSANGULO: tiene
un ángulo obtuso, mayor a 90°.

9. c) TRIANGULO ACUTANGULO: tiene
sus tres ángulos agudos.

10. RECTAS Y PUNTOS NOTABLES EN UN
TRIÁNGULO
Las rectas notables son:
a. Medianas
b. Mediatrices
c. Bisectrices
d. Alturas
De cada una de ellas en cualquier
triangulo son tres.

11. MEDIANA
 Segmento trazado desde un vértice
hasta el punto medio del lado opuesto.

12. MEDIATRIZ
 Perpendicular
trazada en el punto medio
de cada lado.

13. BISECTRIZ
 Recta que partiendo de su vértice
divide al ángulo en dos partes
exactamente iguales.

14. ALTURA
 Perpendicular
trazada desde un
vértice, al lado
opuesto o a su
prolongación. Hay
tres alturas
correspondientes a
cada lado.

15.  Enun triángulo obtusángulo, las alturas
correspondientes a los lados del ángulo
obtuso caen fuera del triángulo, por lo
tanto el ortocentro también.
Ortocentro
Altura Altura
C
A Altura B

16. TRAZOS
 TRAZADO DE UNA BISECRIZ: con
un ángulo cualquiera, con el
compas haciendo centro en el
vértice del ángulo y con una
distancia cualquiera, se
marcan los puntos B y C en los
lados del ángulo; con esa
misma abertura del compas,
haciendo centro en B trazar
un arco D, haciendo lo mismo
con el punto C, se vuelve a
cruzar en el arco D. Uniendo el
vértice del ángulo con el
punto D, se obtendrá la
bisectriz del ángulo.

17.  TRAZADO DE LA
MEDIATRIZ: En un C
segmento cualquiera
abrimos el compas a
más de la mitad del
segmento, y haciendo
centro en los dos
extremos de él, se
trazan los arcos C y D,
a cada lado del
segmento. Se unen los
dos cruces de los arcos
hechos con una recta,
esta será la mediatriz D
del segmento.

18.  PUNTO MEDIO DE UN
SEGMENTO: se sigue
el mismo
procedimiento para
trazar o localizar el
punto medio; solo se
unen los arcos r y n
sobre el segmento
AB y se hará una
marca que será M,
exactamente el
punto medio de un n
segmento .

19. PUNTOS NOTABLES
 Los puntos donde se cortan las rectas notables
en un triangulo son:
1. BARICENTRO:
Centro de
gravedad
del
triangulo
donde se
cortan las
medianas.

20. 2.CIRCUNCENTRO:
punto de
intersección de las
tres mediatrices;
este punto es el
centro del circulo
circunscrito al
triangulo.

21.  INCENTRO:
punto en
donde se
interceptan las
bisectrices, o
sea el centro
del circulo
inscrito del
triangulo.

22.  ORTOCENTRO:
punto donde se
cortan las 3
alturas del
triángulo.

23. PROPIEDADES DE LOS TRIÁNGULOS
I. La altura
correspondiente
a la base de un Altura
triángulo Mediana
isósceles es Mediatriz
Bisectriz
también la
mediana,
mediatriz y
bisectriz de
dicho triángulo.

24. II. En dos triángulos congruentes, a ángulos
congruentes se oponen lados
congruentes y viceversa. Estos lados y
ángulos se llaman homólogos.
III. En todo triángulo, un lado es menor que
la suma de los otros dos y mayor que su
diferencia.
IV. En todo triángulo, a mayor lado se opone
mayor ángulo y viceversa.
V. En dos triángulos que tienen dos lados
respectivamente congruentes, y no
congruente el ángulo comprendido, a
mayor ángulo se opone mayor lado.

25. ALGUNOS TEOREMAS IMPORTANTES
SOBRE TRIÁNGULOS
 TEOREMA 1
La suma de los ángulos interiores de
todo triángulo es igual a dos
ángulos rectos o sea 180°.
x C y
M N
A B

26.  TEOREMA 2 C
Es un COROLARIO
del teorema 1.
La suma de los dos
ángulos agudos
de un triángulo
rectángulo es
igual a un recto
(90°).
B A
<A + <C= 1rt. = 90°

27.  TEOREMA 3
La suma de los C
Z
tres ángulos
exteriores o
externos de
todo triángulo
es igual a 4
ángulos rectos
(360°) Y
A
X B

28.  TEOREMA 4:
Un ángulo
externo de un
triángulo es C
igual a la
suma de los
dos ángulos
internos que
X
no le son
adyacentes.
A B
<X = <A + <C

29. CONGRUENCIA
TRIÁNGULOS CONGRUENTES
Son los que tienen igual forma y
tamaño. Si dos triángulos son
congruentes, sus lados y ángulos
correspondientes son iguales.
C C’
70° 70°
50° 50°
A B A’ B’
60° 60°

30. MARCAS EN LAS PARTES HOMÓLOGAS
 Los
triángulos congruentes se
pueden sobreponer, entonces los
ángulos de un triangulo que
coinciden con el otro se llaman,
ángulos homólogos y los lados que
coinciden serán homólogos.

31. LOS PRINCIPALES CASOS DE CONGRUENCIA DE
TRIÁNGULOS SON 3:
 Siun triangulo tiene dos lados y el
ángulo comprendido congruentes a los
elementos correspondientes de otro,
entonces los dos triángulos son
congruentes.