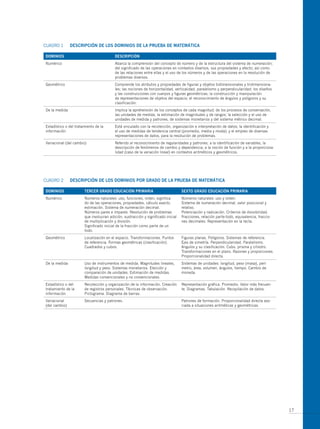
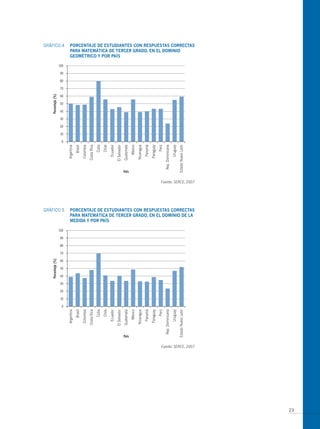
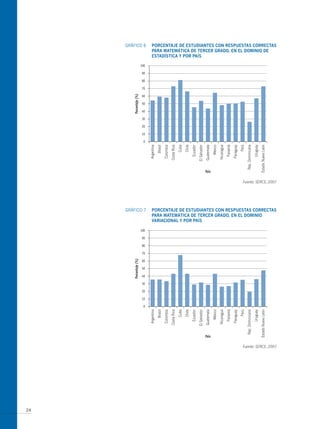
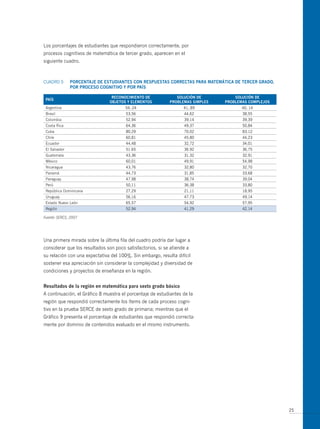
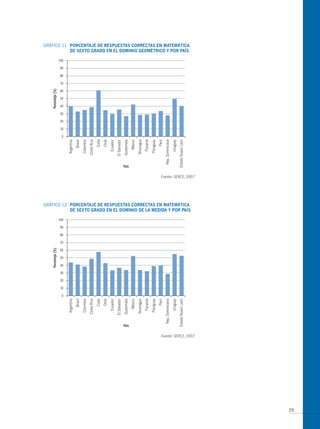
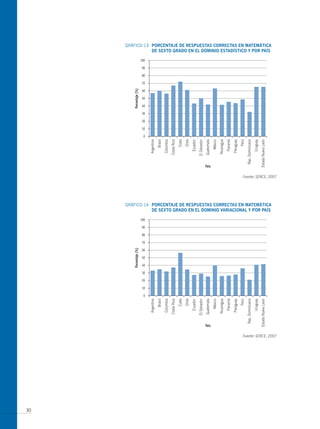
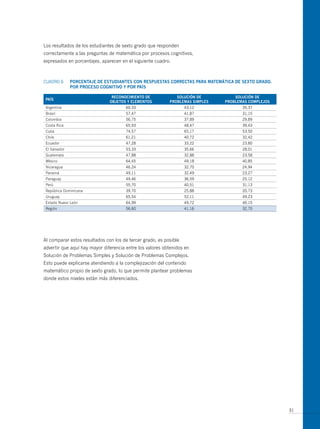
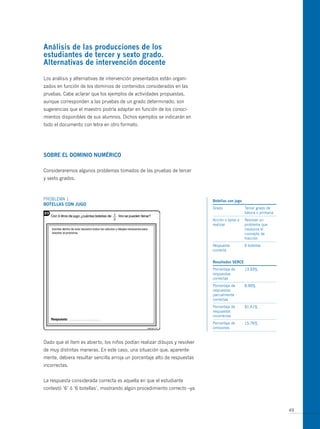
El documento presenta los antecedentes del Segundo Estudio Regional Comparativo y Explicativo (SERCE) realizado por el Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación (LLECE) entre 2002 y 2006, el cual evaluó el desempeño de estudiantes de tercero y sexto grado de educación primaria en las áreas de lenguaje, matemática y factores asociados en varios países de América Latina. Adicionalmente, describe brevemente las pruebas de matemática aplic