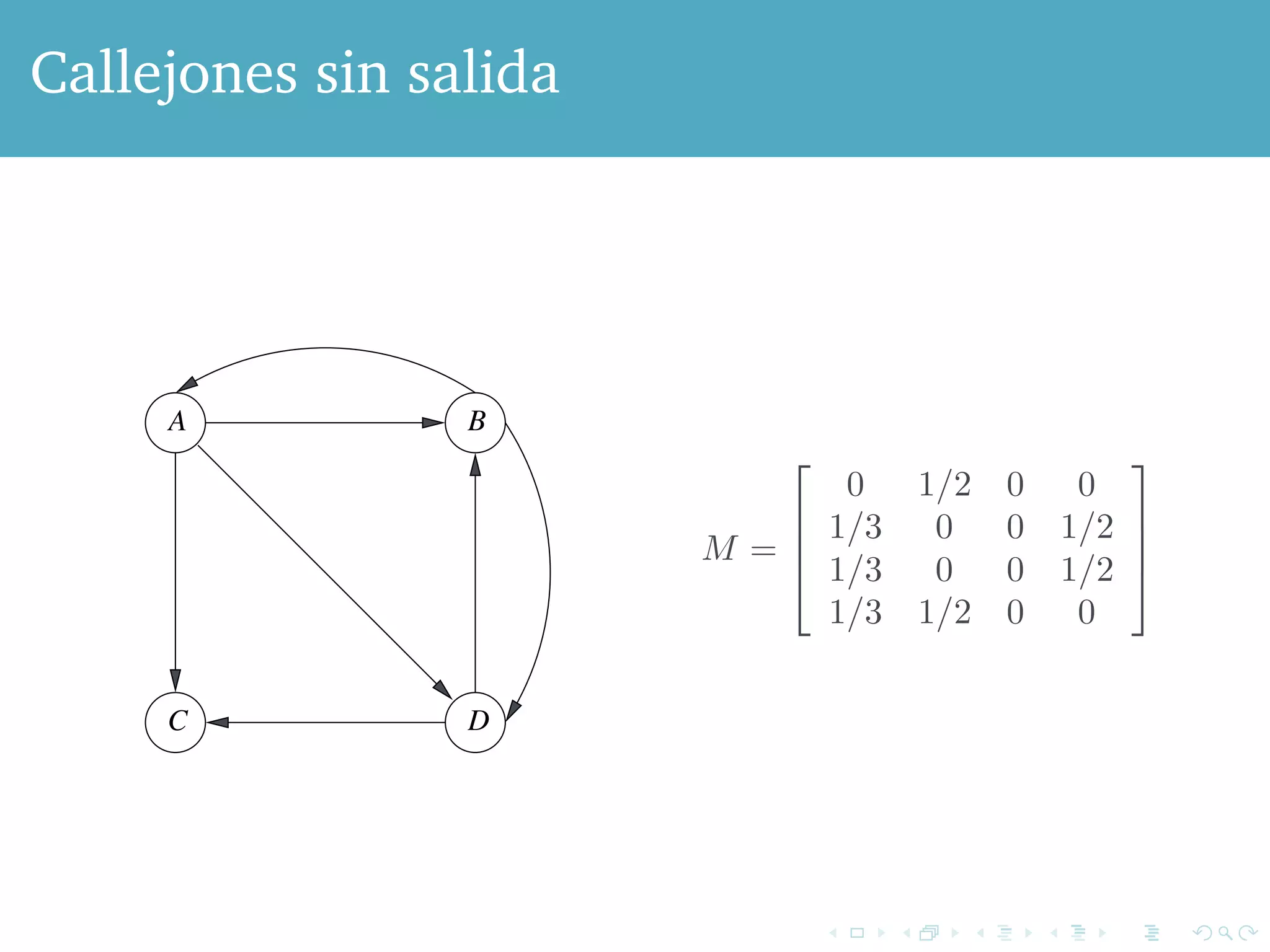
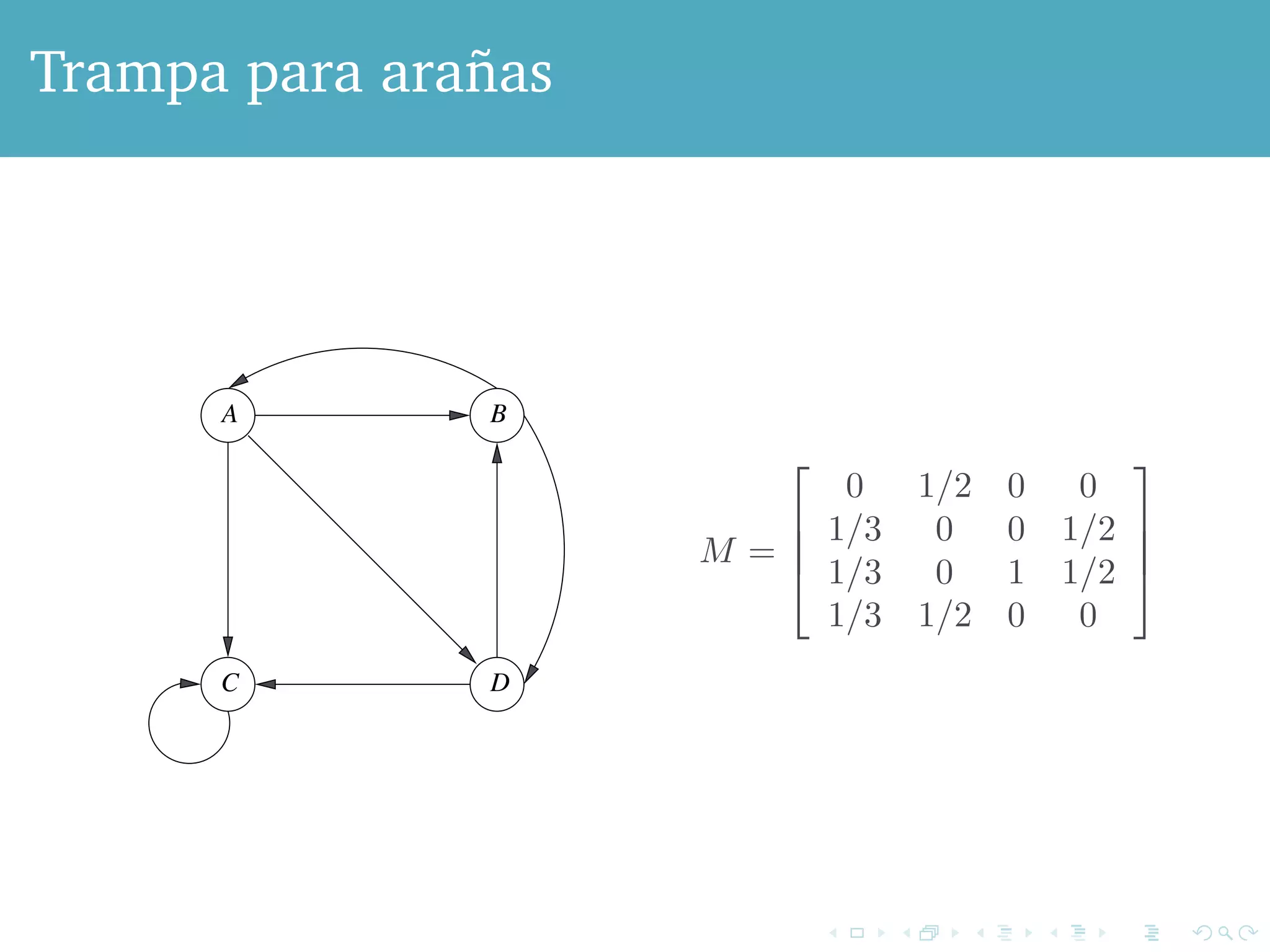
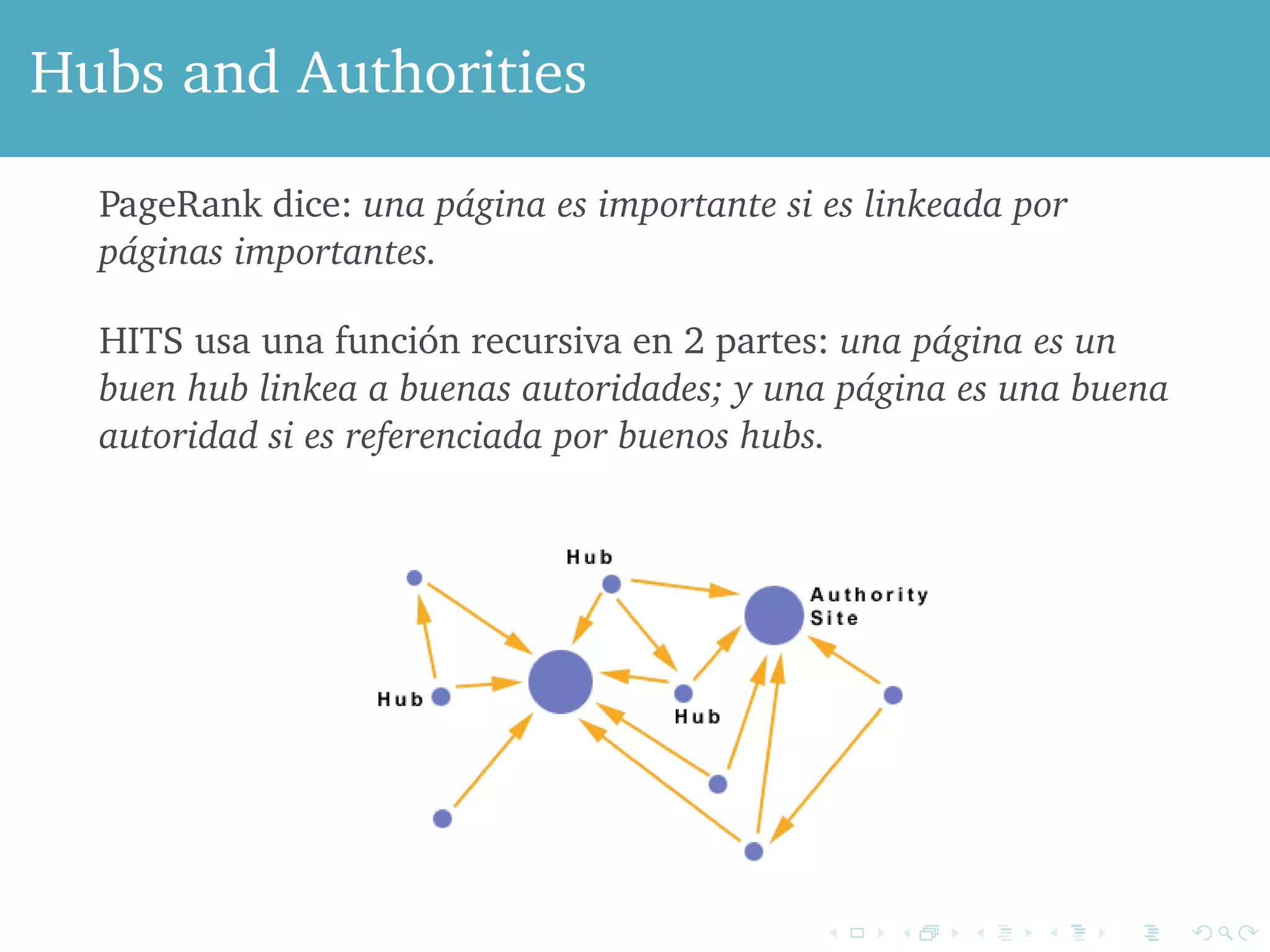
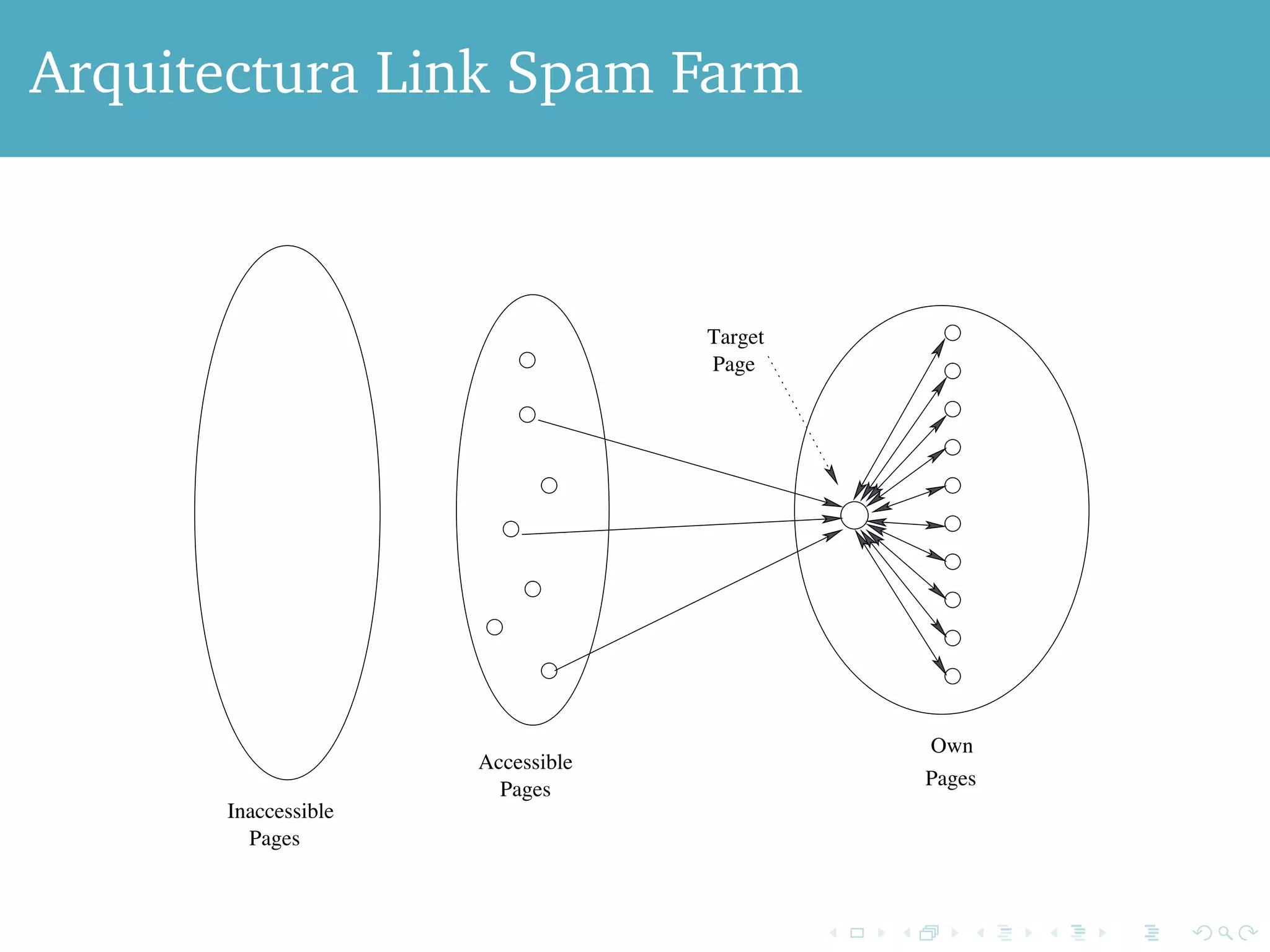
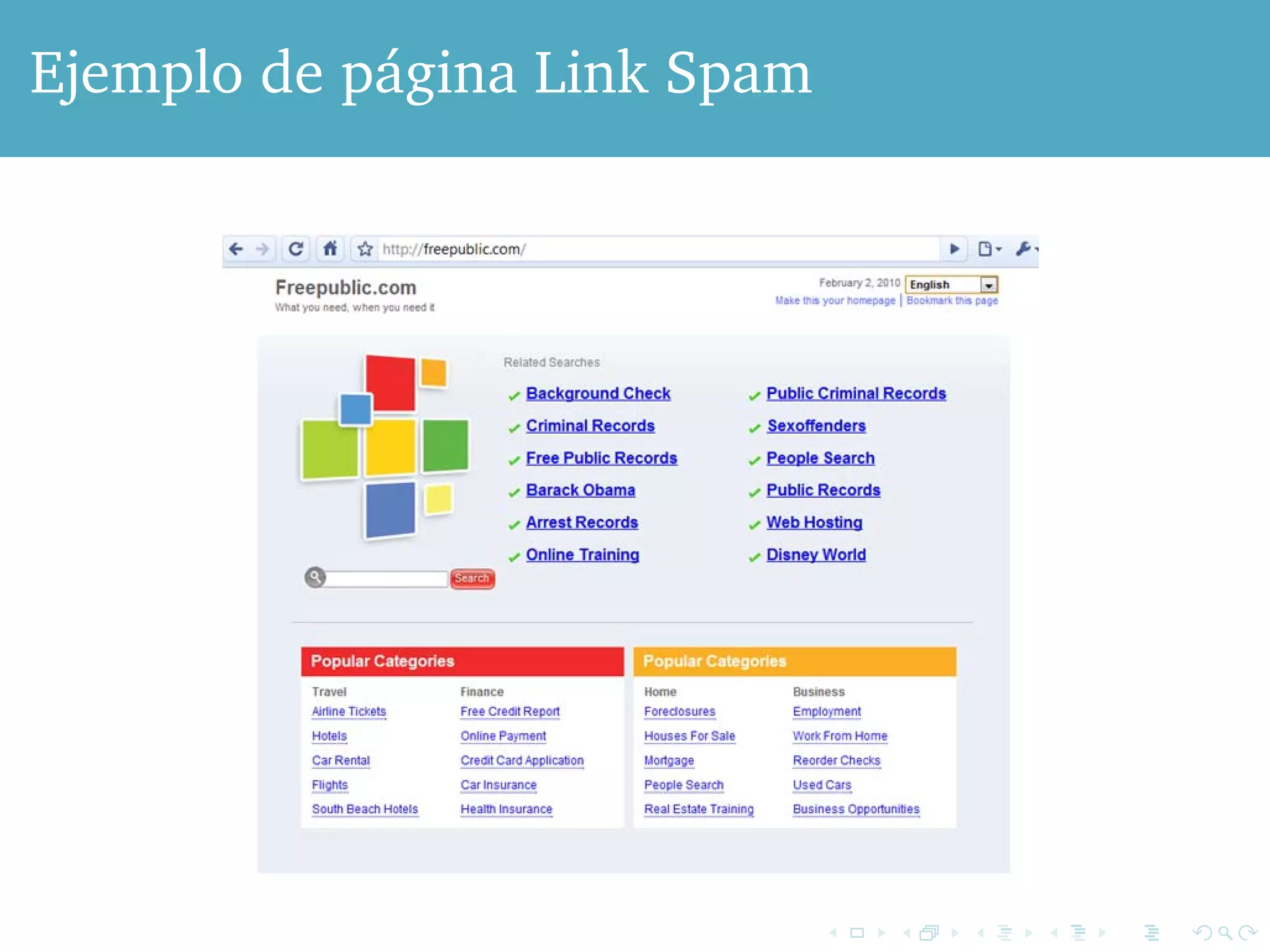
El documento aborda el impacto del algoritmo PageRank, desarrollado por Google, en la mejora de los motores de búsqueda al mitigar el spam. Describe cómo el PageRank asigna relevancia a las páginas web mediante la estructura de enlaces, considerando los enlaces como votos de importancia, y presenta problemas como los callejones sin salida y trampas para arañas que afectan el cálculo del PageRank. Se concluye con soluciones como la estrategia de teleport que permiten manejar estos problemas, asegurando que siempre haya una fracción de usuarios activos en la web.