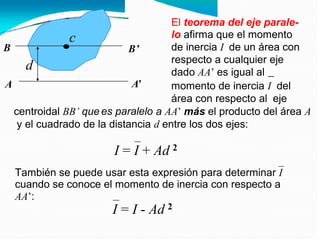
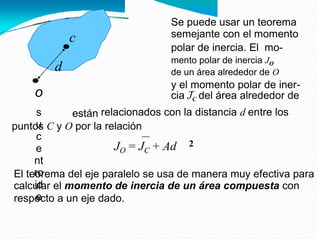
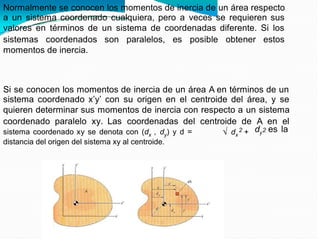
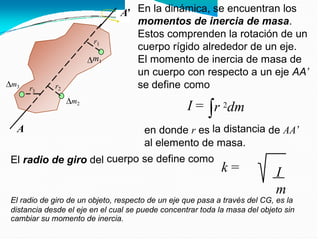
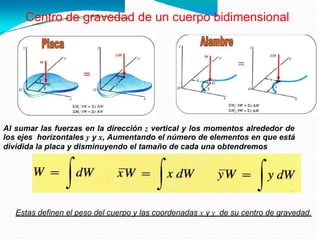
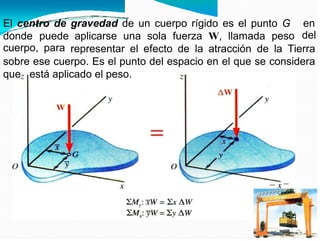
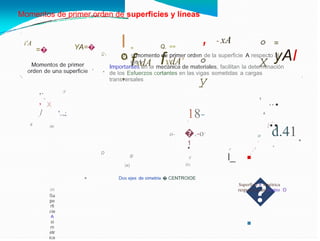
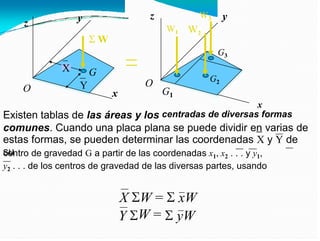
El documento detalla el cálculo del centro de gravedad de cuerpos bidimensionales, enfatizando cómo las fuerzas y momentos se combinan para determinar las coordenadas del centro de gravedad. También aborda los momentos de inercia y su importancia en el análisis mecánico, incluyendo cómo se relacionan con la resistencia de materiales y la dinámica de cuerpos en rotación. Finalmente, se discuten las integrales y fórmulas necesarias para calcular centroides y momentos de inercia para diversas formas geométricas.

2. Centro de gravedad de un cuerpo bidimensional
Al sumar las fuerzas en la dirección z vertical y los momentos alrededor de
los ejes horizontales y y x, Aumentando el número de elementos en que está
dividida la placa y disminuyendo el tamaño de cada una obtendremos
Estas definen el peso del cuerpo y las coordenadas x y y de su centro de gravedad.

3. El centro de gravedad de un cuerpo rígido es el punto G en
del
donde
cuerpo,
puede
para
aplicarse una sola fuerza W, llamada peso
representar el efecto de la atracción de la Tierra
sobre ese cuerpo. Es el punto del espacio en el que se considera
que está aplicado el peso.

4. El peso de un cuerpo no actúa en un solo punto sino
que está distribuido sobre su volumen total, sin embargo
el peso se puede representar con una sola fuerza
equivalente actuando en u punto llamado centro de
masa. Por ejemplo cada parte de un automóvil tiene un
peso propio, pero se puede representar su peso total
con una sola fuerza que actúa en su centro de masa.
Este coincide con el centro de gravedad. Siempre y
cuando actué la fuerza gravitatoria sobre un cuerpo.

5. Centroides de superficies y líneas
llW = pgt M
LW = pgaM
p
g
= den idad (masa por unidad de volumen) del material
2)
= aceleración de la gravedad (9,81
= pe or de la placa
= área del elemento
m/
p = densidad del material
a = área de la sección recta del alambre
1
M
6L longitud del elemento
=
xA = X1 M, + X1 M2 + ... + xn M.,
+ YallA,.
!.M,:
jA = Y1 M, + YzM2 + ···
l:.M,,
: yl
Aumentando et número de elementos en que se divide
la superficie a la vez que se disminuye et tamaño de e/u
= fxdA
lr
A
y y
I
/
-l'
'i:M·xL=Üó.L
l:M�: yL = Iy s:
Alam
bre
'fil¡. xA = ü ÁÁ
�_.: yA = I .1.A
Pla
ca
fiMfi.Nl��-illfNMü .
�rf&��
I�
Estas integrales se conocen como los primeros momentos del área
A con respecto a los ejes y y x, y se denotan por Qy y Qx , X

6. !W =
pgtA!
�w = pgr !
lA
p
g
r
M
= den idad (masa por unidad de volumen) del material
= aceleración de la gravedad (9,81 m/ 2
)�----------------------------,
xA
= espe or de la placa
= área del elemento
yA
Aumentando e número de elementos en que se divide
la superficie a la vez que se disminuye e tamaño de e/u
y y
Jxd
A
xA yA

7. Momentos de primer orden de superficies y líneas
=
yAI
Q, ==
fydA'
/
I
º
·
=
fxdA
- xA
º
X
i'A
'
º
y
YA=�
Q.
=�
Q 1 = momento de primer orden de la superficie A respecto al
eje I
Momentos de primer
orden de una superficie
Importantes en la mecánica de materiales, facilitan la determinación
de los Esfuerzos cortantes en las vigas sometidas a cargas
transversales
' •
.
'-
,.
, ...
.,
/J'
,
'
X
18-
1
/
I ..
d.41
·
'..,; A
'
,
/
B
(a)
�.-o·
1
o- o
/ •
·
�
·
• J
-r
l_
I
D I
B' 8'
(b)
(a)
• Dos ejes de simetria � CENTROIOE
Superficie A simétrica
respecto a un centro O
(bl
Su
pe
rfi
cie
A
si
m
étr
ica

8. Placas y alambres compuestos
+
w,
+ w,
+
x,w,
+ ¡2w2
+
x.w.
+ f.W.
= .f1W1
= ¡,w,
'
Si la placa es HOMOGENEA y de espesor uniforme
X(W,
Y<
W,
+ ··· + W.)
W.
>
+
M,:
+ x,A,
+
+ y,A2 +
+
x.,A,
+
Y.A.
Q, = X(A, + A2 + +A.)=
x,A,
+ ... + +
'f.M,:
' Q, = Y(A, + A2 + + A.) = y,A,
w,
;• A,
,v, -"
L'
w
.
G,
e,•
X X
-
Yl:W l:yW
Xl:W = XI:A - I:.iA
Q
Y
z y
X A
- +
.xA
-
+
-
A 1 Semicírculo
A2 Rectángulo
entero
A3 Orificio circular
X
+
+
+
-

9. W3
W2
z y
y
z
W1
W
G3
X G
G2
O
Y
O G
x 1
x
centradas de diversas formas
Existen tablas de las áreas y los
comunes. Cuando una placa plana se puede dividir en varias de
estas formas, se pueden determinar las coordenadas X y Y de
su
centro de gravedad G a partir de las coordenadas x1, x2 . . . y y1,
y2 . . . de los centros de gravedad de las diversas partes, usando
X W =
W =
xW
Y yW

10. y
z
G
O
x
Si la placa es homogénea y de espesor uniforme, su centro
de gravedad coincide con el centroide C del área de la
misma y los primeros momentos del área compuesta son
Qy = X A = xA Qx = Y A = yA

11. y
Cuando el área está limitada por curvas analíticas, se
pueden determinar por integración las coordenadas de su
centroide. Esto se puede hacer al evaluar integrales dobles
o una sola integral en la cual se use un elemento de área,
rectangular delgado o con forma de pastel. Denotando por
xel y yel las coordenadas del centroide del elemento dA, se
tiene
Qy = xA = xel dA Qx = yA = dA
el

12. Tabla de centroides de figuras simples
Forma y Área
X
1
h
_
h
3
bh
2
Á.rea triangular
�f¿+Q ..¡
2 2
4r
31
7'
'1f'·
i4
4
..1!
:.
3'
11
'
Un cuarto de área
circular
4r
31
7'
'1f'r2
2
o
Area semicircular
0
1
4b
3'
11
'
•
'Tf'a
b
4
4a
3-
.,
.
Un cuarto de área
elíptica
b
.l..
.o
,
4b
31
7'
7mb
2
.Áre
a
semí
olípti
ca
º1- a --l ()
X
1-a--¡ 31
1
5
Área
semí
parab
élica
2ah
3
3
a
8
T
h
.l
..
o
-j r
3h
5
4<1
h
3
o
Area parabólica

13. ah
3
3h
10
3a
4
Enjuta parabólica
1-+-----a---�
t ah
n+
l
n+l �h
411 + 2
--a
Enjuta general n+2
2rsen
a
3a
o
Sector circular
Figuta 5.8A Centroides de áreas comunes.

14. -
y Longitud
Fonna .r
·Jr
r
,
,--- j
¡; n cuarto de arco
circular
1
2r
2r
,
�
1Tr
2
- -
1
T
1
T
ºL _ _ _
o -2r
k- o
Arco semicircular 1Tr
1T
X
------
_-
r
r;�-
�
�
- e rsena
o
--
-
º1.----:
-"---
Arco de círculo 2.ar
- a
X
Figura 5.88 Centroides de formas comunes de líneas.

15. L Los teoremas de Pappo-Guldino
relacionan la determinación del
área de una superficie de
revolución o del volumen de un
cuerpo de revolución con la
determinación del centroide
de la curva o área generadoras. El
área A de la superficie generada al
hacer girar una curva de longitud L
alrededor de un eje fijo es
C
y
x
2 y
A = 2 yL
en donde y representa la distancia del centroide C de la
curva al eje fijo.

16. C
A
y
x
2 y
El volumen V del cuerpo generado al hacer girar un área
A alrededor de un eje fijo es
V = 2 yA
en donde y representa la distancia del centroide C del
área al eje fijo.

17. w
w
x
B
O
B x
O P
dx
x
L
L
También se puede usar el concepto de centroide de un área para
resolver problemas diferentes a los de tratar con el peso de
placas planas. Por ejemplo, para determinar las reacciones en los
apoyos de una viga, se reemplaza una carga distribuida w por
una carga concentrada W con magnitud igual al área A debajo de
la curva de carga y que pase a través del centroide C de esa
área. Se puede usar el mismo enfoque para determinar la
resultante de las fuerzas hidrostáticas ejercidas sobre una placa
rectangular sumergida en un líquido.
x
W
C W = A
dW
w

18. x y z
x y z
Las coordenadas del centro de gravedad G de un cuerpo
tridimensional se determinan a partir de
xW = dW yW = dW zW = dW
Para un cuerpo homogéneo, el centro de gravedad G coincide
con el centroide C del volumen V del mismo; las coordenadas
de C se definen por las relaciones
xV = dV yV = dV zV = dV
Si el volumen posee
estará en ese plano;
un plano de simetría, su centroide C
si posee dos planos de simetría, C estará
localizado sobre la recta de intersección de los dos planos; si
posee tres planos de simetría que se intersequen en un solo
punto, C coincidirá con ese punto.

19. y
15mm
r30mm
1
I e
X
80mm
u
40mm
30mm�,
Lw
mm
40
15mm
Fig. PS.25

20. Determinación de CENTROIDES por integración
1�
= fxdA
X
1
1
1
l
y
lL.....L---
11�-
o�a� z
o dx X
.ia1•
2r
cot9
f.. --
a+
z-z
3
1-, • X
,.. -,
4.4 • (a-z)d)'
(b)
J.. • 2r
acn9
,.. - yfl
4.4 •ydx
(a)
3
4.
4
•
+
r
d
9
(e)
1 y
= J1
2
+ (:)
dy
_, dL
-z
dL =
J,2
2
+ (:;) d8
oL------1c._ _
z
QL----L....:::...--
yL = fy dl:
= fxdL
n:

21. fXe1 dA
XA
fYet
yA dA
o )'
-,r= X y
1- ...............---
-J�
O��=!_j X
.fil, =--r-
4l +.x:
y._, ;¡:
y

22. Vigas con cargas DISTRIBUIDAS
w
w
w
dW
W-'> [N/m]
W=A
-
(OP)W = fxdW
ldw = wdx = dA y
W
=
Al
W= fdA (¡)A - J:xdA tjXA
- fxdA
-
=A
X

23. MOMENTOS DE INERCIA
Las cantidades llamadas momentos de inercia aparecen con frecuencia en
los análisis de problemas de ingeniería. Por ejemplo, los momentos de
inercia de áreas se utilizan en el estudio de las fuerzas distribuidas y en el
cálculo de deflexiones de vigas. El momento ejercido por la presión sobre
una placa plana sumergida se puede expresar en términos del momento de
inercia del área de la placa. En dinámica, los momentos de inercia de masa
se usan para calcular los movimientos rotatorios de objetos.
Los momentos de inercia de un área son integrales de forma similar a las
usadas para determinar el centroide de un área. El momento de Inercia es
una medida de la distribución del área respecto a un eje dado.

24. El momento de inercia
inercia respecto a dos
respecto a un punto es la suma de los momentos de
ejes perpendiculares entre sí, contenidos en el plano,
que se cortan en dicho
y
Los momentos rectangulares
de inercia Ix e Iy de un área se
definen como
y 2dA x 2dA
Ix = Iy =
dx x
El momento de inercia respecto a un punto es igual al momento de
inercia respecto a un eje perpendicular a la figura, que pase por dicho
punto. También será igual al momento de inercia respecto a un plano
perpendicular a él que le corte en dicho eje.
La inercia es la propiedad de la materia que hace que ésta resista a
cualquier cambio en su movimiento, ya sea de dirección o de
velocidad
y
x

25. El momento polar de
inercia de un área A
con
respecto al polo O
define como
se
r 2dA
JO =
La distancia de O al elemento de área dA es r. Observando
que r 2 =x + y
2 2, se establece la relación
JO = Ix + Iy
y
dA
r y
O x x
A

26. El radio de giro de un
área A con respecto al
eje x se define como la
distancia kx, en donde
2
Ix = kx A. Con definiciones
semejantes para los
radios de giro de A con
respecto al eje y y
con respecto a O, se tiene
JO
Ix Iy
kO =
kx = ky =
A
A A
El radio de giro es una medida de la
Inercia
distribución del area respecto al eje de
y
A
kx
O x

27. Tablas de Momentos de Inercia

28. Teorema de los ejes paralelos
Si se conoce el momento de Inercia de un área alrededor
de un eje que pasa por su Centroide, conviene determinar
el momento de inercia
paralelo
del área en torno
teore
ma
a un eje
Correspondiente
paralelos.
usando el de ejes
Esto establece que el momento
es igual al
de inercia de un área
alrededor de un eje Momento de inercia del
área en torno
más
a un eje paralelo que pasa a través del
centroide el producto del área y el cuadrado de la
distancia perpendicular entre los ejes.
Esto permite transferir el momento de
respecto a su eje centroidal al eje que
así la Inercia Total.
inercia de cada parte
pasa por G y obtener

29. El teorema del eje parale-
lo afirma que el momento
de inercia I de un área con
respecto a cualquier eje
dado AA’ es igual al
c
B B’
d
A’
A momento de inercia I del
área con respecto al eje
centroidal BB’ que es paralelo a AA’ más el producto del área A
y el cuadrado de la distancia d entre los dos ejes:
2
I = I + Ad
También se puede usar esta expresión para determinar I
cuando se conoce el momento de inercia con respecto a
AA’:
2
I = I - Ad

30. Se puede usar un teorema
semejante con el momento
c
polar de inercia. El mo-
mento polar de inercia JO
de un área alrededor de O
y el momento polar de iner-
cia JC del área alrededor de
relacionados con la distancia d entre los
d
o
s
u
c
e
nt
ro
id
e
están
puntos C y O por la relación
2
JO = JC + Ad
El teorema del eje paralelo se usa de manera muy efectiva para
calcular el momento de inercia de un área compuesta con
respecto a un eje dado.

31. El producto de inercia
área A se define como
de un
Ixy = xy dA
I = 0 si el área A es
xy
simétrica con respecto a
cualquiera de los ejes de
coordenadas o a ambos.
El teorema del eje paralelo para los productos de inercia es
Ixy = Ix’y’ + xyA
en donde Ix’y’ es el producto de inercia del área con respecto a
los ejes centroidales x’ y y’, los cuales son paralelos a los ejes x
y y, y x y y son las coordenadas del centroide del área.
y
y’
x’
O
x

32. Normalmente se conocen los momentos de inercia de un área respecto
a un sistema coordenado cualquiera, pero a veces se requieren sus
valores en términos de un sistema de coordenadas diferente. Si los
sistemas coordenados son paralelos, es posible obtener estos
momentos de inercia.
Si se conocen los momentos de inercia de un área A en términos de un
sistema coordenado x’y’ con su origen en el centroide del área, y se
quieren determinar sus momentos de inercia con respecto a un sistema
coordenado paralelo xy. Las coordenadas del centroide de A en el
dy es la
2 2
sistema coordenado xy se denota con (dx , dy) y d =
distancia del origen del sistema xy al centroide.
dx +

33. En la dinámica, se encuentran los
momentos de inercia de masa.
Estos comprenden la rotación de un
cuerpo rígido alrededor de un eje.
El momento de inercia de masa de
un cuerpo con respecto a un eje AA’
A’
r1
m1
se define como
I =
m3 r2
r3
m2
r 2dm
la distancia
A en donde r es de AA’
al elemento de masa.
cuerpo se define como
El radio de giro del
k = I
m
El radio de giro de un objeto, respecto de un eje que pasa a través del CG, es la
distancia desde el eje en el cual se puede concentrar toda la masa del objeto sin
cambiar su momento de inercia.

34. Los momentos de inercia de masa con respecto a los ejes de
coordenadas son
2 2
Ix
Iy
Iz
=
=
=
(y
(z
+
+
z
x
y
)
)
)
dm
dm
dm
2 2
2 2
(x +
A’
También se aplica el teorema del eje
paralelo a los momentos de inercia de
masa.
d
B’
2m
I = I + d
A I es el momento de inercia de masa
con respecto al eje centroidal BB’,
el cual es paralelo al eje AA’. La
masa del cuerpo es m.
G
B

35. La Inercia de un elemento de àrea.
El momento de inercia de área plana respecto a un eje
de su plano será el producto del área del elemento por
el cuadrado de su distancia a ese eje. El momento de
Inercia se conoce también como momento estático de
segundo orden y también como segundo momento.
y 2dA Iy = x 2dA
incercia de todos
Ix =
La Inercia de un área es la suma de los momentos de
sus elementos asi:
∫ y 2dA x 2dA
Ix = Iy = ∫

36. El procedimiento para determinar el momento de inercia en
aéreas
compuestas es:
1. Divida en figuras simples. Usando croquis indique la distancia
perpendicular a partir del centroide de cada parte del eje de
referencia.
El momento de inercia de cada parte deberá calcularse en
torno a su eje centroidal que sea paralelo al eje de referencia.
Para el calculo use tabla de inercias. Si el eje centroidal no
coincide con el eje de referencia deberá de calcularse por el
teorema de los ejes paralelos, para determinar el momento
de inercia de la parte en torno al eje de referencia.
2.
3. El momento de inercia de toda el área alrededor del eje de
referencia se determina sumando los resultados de las partes
componentes. Si fuese un agujero este se restará.

37. En resumen…

38. Bibliografía Consultada
Mecánica para estudiantes de Ingenieria. Branson,Lane K.
Física Fundamental. Valero, Michel. Editorial Norma, Bogotá – Colombia.
1986
Estática. Mecánica para ingeniería Bedford, Anthony – Fowler, Wallace
Editorial Progreso, México DF. 200
Dinámica. Mecánica para ingeniería
Editorial Progreso, México DF. 200
Fundamentos de Física. Tomo
1, Sexta Frederick J. Buecche –
David A. Jerde S.A. México. 1995
Bedford, Anthony – Fowler, Wallace
edición
McGraw – Hill Interamericana Editores
Manual de Mecanica Aplicada. MEDIOS DIDÁCTICOS. INACAP
Apuntes Estática. Jorge Enrique Meneses Flórez. Universidad de Chile.
Beer, Ferdinand; Johnston, Russell. “Mecánica vectorial para ingenieros:
Estática”, 6ta ed. Mc – Graw Hill, México. 1997.
James M. Gere “Mecánica de Materiales”
Quinta Edición, Editora. Thomson Learning , 2002
Mecànica vectorial Estática y Dinámica. Shaum. E.W. Nelson, C.L. Best, W.
G.
Mc. Lean. 5Tha Edición. Mc. Graw Hill.