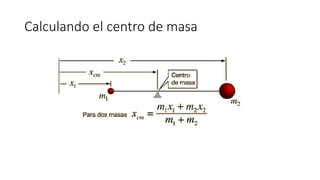
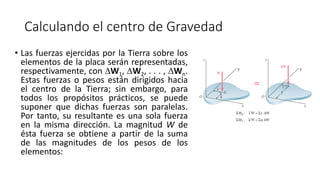
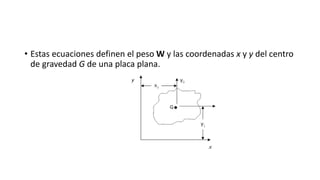
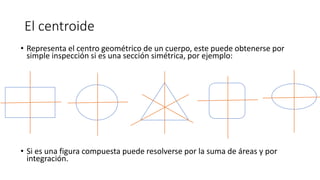
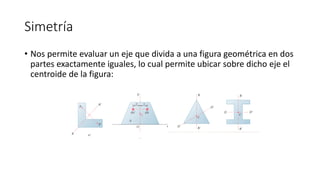
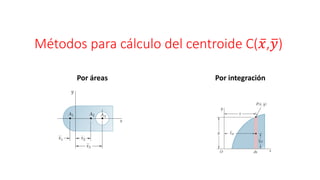
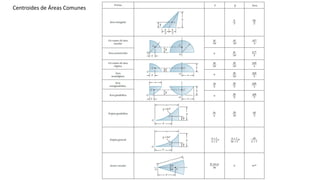
El documento aborda conceptos sobre centroides, centro de gravedad y centro de masa, explicando sus diferencias y métodos de cálculo. Se discute la importancia de estos conceptos en la ingeniería para analizar fuerzas distribuidas y momentos en cuerpos rígidos. Además, se presentan técnicas para encontrar centroides mediante descomposición en áreas conocidas y métodos de integración.

1. Centroides e Inercias

2. Tema: Centroides
Conceptos Generales y métodos de cálculo

3. Introducción
• Sabemos que el peso es la fuerza que ejerce la tierra sobre un cuerpo. El
peso es un vector que se ubica en la partícula más representativa del
cuerpo denominada centro de gravedad. Bajo condiciones de uniformidad,
este centro coincide con el centro de masa y con condiciones de simetría-
geometría, por lo cual le llamamos comúnmente centroide a tal punto de
interés.
• El objetivo del estudio de los centroides es el análisis de fuerzas
distribuidas a lo largo de un cuerpo rígido, mediante un procedimiento de
cálculo de áreas e integración que permitirá incluir en el análisis de fuerzas
y momentos a estas cargas denominadas distribuidas, dándoles un punto
de aplicación (centroide) y una magnitud (área), que son los elementos
primordiales para la obtención de resultantes.

4. Conceptos Básicos
Inicialmente debemos reconocer la diferencia entre los siguientes
conceptos:
• Centro de Gravedad: En dicho punto, se aplica la resultante de
las fuerzas gravitatorias que ejercen su efecto en un cuerpo.
• Centro de masa: Depende de la distribución de la materia, se
utiliza para calcular la respuesta dinámica ante la inercia de un
cuerpo.
• Centroides: es un punto que define el centro geométrico de un
objeto

5. Suposición Básica
• En nuestros estudios de Ingeniería se asume que el cuerpo se
encuentra en “condición ideal”, es decir, el campo gravitatorio es
uniforme y el objeto motivo de estudio es homogéneo; luego el
centro de gravedad, el centro de masa y el centroide coinciden en un
mismo punto.
• Para esta suposición se toman en cuenta las siguientes condiciones:
1. El cuerpo rígido es de un material homogéneo (no cambia su densidad)
2. El espesor del elemento de análisis se asume uniforme
3. Hay simetría o uniformidad en el campo gravitatorio (la atracción de la
gravedad es constante)

6. El centro de masa
• En física, además del centro de gravedad aparecen los conceptos de centro
de masa y de centro geométrico o centroide que, aunque pueden
coincidir con el centro de gravedad, son conceptualmente diferentes.
• Centro de masa y centro de gravedad: El centro de masa coincide con el
centro de gravedad sólo si el campo gravitatorio es uniforme; es decir,
viene dado en todos los puntos del campo gravitatorio por un vector de
magnitud y dirección constante.
• Centro geométrico (Centroide) y centro de masa: El centro geométrico de
un cuerpo material coincide con el centro de masa si el objeto es
homogéneo (densidad uniforme) o cuando la distribución de materia en el
sistema es simétrico.

7. Calculando el centro de masa

8. El centro de gravedad
• Es el punto de aplicación de la resultante de todas las fuerzas de
gravedad que actúan sobre las distintas porciones materiales de un cuerpo,
de tal forma que el momento respecto a cualquier punto de esta resultante
aplicada en el centro de gravedad es el mismo que el producido por los
pesos de todas las masas materiales que constituyen dicho cuerpo.
• En otras palabras, el centro de gravedad de un cuerpo es el punto respecto
al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos
materiales que constituyen el cuerpo producen un momento resultante
nulo.
• El centro de gravedad de un cuerpo no corresponde necesariamente a un
punto material del cuerpo. Así, el c.g. de una esfera hueca está situado en
el centro de la esfera que, obviamente, no pertenece al cuerpo

9. Calculando el centro de Gravedad
• Considere una placa plana
horizontal. La placa puede dividirse
en n elementos pequeños. Las
coordenadas del primer elemento
se representan con x1 y y1, las del
segundo elemento se representan
con x2 y y2, etc.

10. Calculando el centro de Gravedad
• Las fuerzas ejercidas por la Tierra sobre los
elementos de la placa serán representadas,
respectivamente, con W1, W2, . . . , Wn.
Estas fuerzas o pesos están dirigidos hacia
el centro de la Tierra; sin embargo, para
todos los propósitos prácticos, se puede
suponer que dichas fuerzas son paralelas.
Por tanto, su resultante es una sola fuerza
en la misma dirección. La magnitud W de
ésta fuerza se obtiene a partir de la suma
de las magnitudes de los pesos de los
elementos:

11. Calculando el centro de Gravedad
Fz: W = W1 +
W2+…+ Wn
• Para obtener las coordenadas
x y y del punto G, donde debe
aplicarse la resultante W, se
escribe que los momentos de
W con respecto a los ejes y y
x son iguales a la suma de los
momentos correspondientes
de los pesos elementales,
esto es:

12. Calculando el centro de Gravedad
My: ҧ
𝑥W = x1 W1 + x2 W2 +…+ xn Wn
Mx: ത
𝑦W = y1 W1 + y2 W2 +…+ yn Wn
• Si ahora se incrementa el número de
elementos en los cuales se ha dividido la
placa y simultáneamente se disminuye el
tamaño de cada elemento se obtienen, en
el límite, las siguientes expresiones:
W =‫׬‬ 𝑑𝑊 ҧ
𝑥W =‫׬‬ 𝑥𝑑𝑊 ത
𝑦W =‫׬‬ 𝑦𝑑𝑊

13. • Estas ecuaciones definen el peso W y las coordenadas x y y del centro
de gravedad G de una placa plana.

14. El centroide
• Representa el centro geométrico de un cuerpo, este puede obtenerse por
simple inspección si es una sección simétrica, por ejemplo:
• Si es una figura compuesta puede resolverse por la suma de áreas y por
integración.

15. Simetría
• Nos permite evaluar un eje que divida a una figura geométrica en dos
partes exactamente iguales, lo cual permite ubicar sobre dicho eje el
centroide de la figura:

16. Calculando
el centroide

18. Primeros momentos de áreas (Qx , Qy)
• La integral ‫׬‬ 𝑥𝑑𝐴 se conoce como el primer momento del área A
con respecto al eje y y se representa con Qy. En forma similar, la
integral ‫׬‬ 𝑦𝑑𝐴 define el primer momento de A con respecto al eje x y
se representa con Qx. Así se escribe:

19. Métodos para cálculo del centroide C( ҧ
𝑥,ത
𝑦)
Por áreas Por integración

20. Preguntas
1. ¿Qué es centro de gravedad y cómo se calcula?, ¿Cuál es su
utilidad?
2. ¿Qué es centro de masa y cómo se calcula?, ¿Cuál es su utilidad?
3. ¿Qué es centroide y cómo se calcula?, ¿Cuál es su utilidad?
4. ¿Bajo qué condiciones puedes suponer que centro de gravedad,
centro de masa y centroide es el mismo punto?
5. ¿Qué significa primer momento de área?, ¿cómo se calcula?, ¿para
qué sirve?

21. Método de áreas compuestas

22. Centroides de Áreas Comunes

23. Cálculo de Centroides por el Método de Áreas
Compuestas
• El método consiste en la descomposición el elemento de análisis en figuras geométricas conocidas,
considerando la densidad o peso específico del material constante, se iguala la ubicación del centro de
gravedad con el centroide, por lo que el cálculo se simplifica a la obtención de áreas de cada figura y
ubicación de su centroide específico y luego su valor promedio.
• Fórmulas:

24. Procedimiento:
1. Distribuya el cuerpo en áreas de geometría conocida: Triángulos, rectángulos, semi círculos,
etc.
2. Enumere cada una de las figuras en el esquema
3. Obtenga de forma detallada de cada una: Su área, y la ubicación de su centroide particular
desde un punto de referencia especificado, por ejemplo en la figura anterior ҧ
𝑥 𝑦 ത
𝑦 se
referencian desde el punto O
4. Es importante que áreas huecas se consideran negativas
5. También considerar que en los puntos a la izquierda y abajo del origen, ҧ
𝑥 𝑦 ത
𝑦 se consideran
negativos:
6. Luego trasladar todos los datos a un cuadro resumen donde se suman por columna: Los
datos de la primera columna se toman del dibujo, los de la segunda, tercera y cuarta del
cálculo (para el cual pueden usar las tablas anexas), las dos ultimas columnas se obtienen
multiplicando segunda con tercera o segunda con cuarta columna, así también las
unidades, respectivamente. Las sumatorias solo se requieren de la segunda, quinta y sexta
columna.
7. Los resultados de las sumatorias son numerador y denominador, que irán a las fórmulas:
ҧ
𝑥 =
σ𝑖=1
𝑛
ҧ
𝑥𝐴
σ𝑖=1
𝑛 𝐴
ത
𝑦 =
σ𝑖=1
𝑛
ത
𝑦𝐴
σ𝑖=1
𝑛 𝐴
8. Las coordenadas del Centroide serán: C( ҧ
𝑥 , ത
𝑦)

25. Figura 𝐴 ҧ
𝑥 ത
𝑦 ҧ
𝑥 𝐴 ത
𝑦 𝐴
1
2
3
= -------- =

26. Ejemplo: Obtenga las coordenadas del centroide de la figura mostrada.

28. • Determine el centroide del área mostrada

29. Primer Paso
• Dividimos la figura en elementos geométricos
y los enumeramos:
1
2

30. Segundo paso
Obtenemos de cada figura el área, ҧ
𝑥, ത
𝑦, recordando que estas
coordenadas van desde el origen.

31. Tercer paso: llenamos la tabla

33. Listo!

34. Cálculo de Centroides por el
método de integración

35. Método de integración
• Se aplica para obtener las coordenadas del centroide del área bajo
una curva que se comporta según la ecuación especificada, o que
puede obtenerse en el análisis matemático de su comportamiento.

37. Ejemplo

38. Primer paso: Obtener las ecuaciones para
cada sección ó área:

39. Segundo paso: Definir el elemento diferencial a
trabajar: Vertical u horizontal (depende desde que
eje se proyecta el área)

40. Tercer paso: Cálculo de las integrales según
delimitación

41. Si hubiéramos trabajado el elemento
horizontal sería:

42. Ejercicios:
Resolver
obteniendo
por
integración
el centroide
de las
siguientes
figuras:

43. Algunas respuestas:

44. genial!