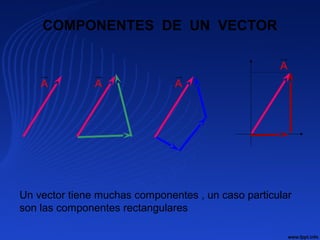
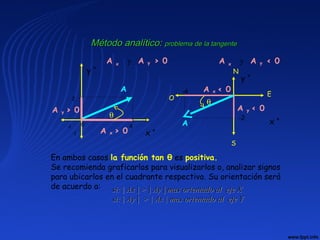
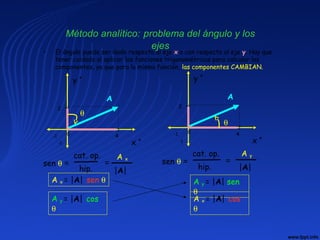
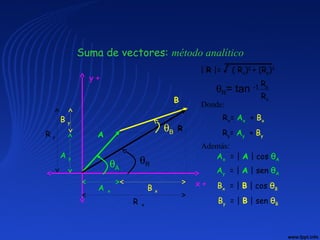
El documento proporciona un resumen de la historia de la física desde sus orígenes hasta el siglo XXI. Comienza describiendo los primeros avances en Egipto y Grecia antigua, luego menciona figuras clave como Arquímedes, Kepler, Galileo y Newton. Explica que la física se dividió en clásica y moderna, con Einstein y la teoría cuántica transformando el campo en el siglo XX. Concluye que se esperan mayores avances en el siglo XXI.

1. CURSO DE FÍSICA I
MECÁNICA
MSc. WILLIAM MURILLO LÓPEZMSc. WILLIAM MURILLO LÓPEZ
wmlopez@gmail.com

2. BREVE HISTORIA DE LA FÍSICA
La física es una ciencia que surgió desde que el hombre existe
en la tierra. Los egipcios construyeron las pirámides de Gizeh
alrededor del año 3000 A.C. orientándolas de tal manera que
cada una de sus caras esta colocada frente a cada punto
cardinal. Los inicios de la astronomía pueden situarse en Grecia
en el siglo VI A, .C. Algunos personajes asociados a la historia de
la física son:
 Tales de Mileto (-640 a -547) estudio los eclipses,
consideraba que la tierra era un disco flotando en un océano.
 Filolao (Fines del siglo V A.C.) descubre que los astros son
esféricos, y los planetas giran alrededor del sol.
 Heráclito (-540 a -480) propone que el calor es una fuerza en
la que esta el origen de las transformaciones de los cuerpos.

3.  Durante largo tiempo, el hombre conoció la electricidad estática,
es decir, de los cuerpos cuya carga eléctrica esta en equilibrio y
la electricidad en movimiento.
 Arquímedes (287 a 212 A.C.) estudió el centro de gravedad, la
teoría de la palanca y del plano inclinado, el principio de
flotabilidad de los cuerpos, el polipasto, el tornillo y maquinas de
guerra. Realizó estudios de óptica, mecánica e hidrostática.
 En el año 300 A.C. se consideraba que la tierra se movía
alrededor del sol, aunque predominaba la idea de que la tierra
era el centro del universo. Paso mucho tiempo hasta el año
1500 en que se realizaron estudios experimentales de física.
 Johannes Kepler obtuvo las leyes con las que podía dar
explicación respecto al movimiento de los planetas alrededor del
sol.

4.  Galileo Galilei (1564-1642) Estudió el movimiento de los astros y
las leyes de la mecánica, invento el telescopio para observar el
movimiento de los planetas y sus satélites así como las manchas
solares.
 Isaac Newton en 1687 describe las leyes de la dinámica conocidas
como leyes de Newton y la ley de la gravitación universal.
 En el siglo XVIII se estudió la termodinámica, en el siglo XIX se
estudió la electricidad y el magnetismo.
 Roentgen descubrió en 1895 los rayos X, los cuales eran ondas
electromagnéticas de frecuencias muy altas.
 Pierre Curie y Marie Curie realizaron estudios de la radioactividad
dando comienzo a la física nuclear y al estudio de la estructura
microscópica de la materia.
 En el siglo XX el desarrollo de la física promovió el desarrollo
tecnológico con el descubrimiento de la teoría de la relatividad y el
comienzo de la mecánica cuántica.

5.  Albert Einstein formuló en 1905 la teoría de la relatividad y realizo
estudios que relacionan la energía y la materia.
 Rutherford realizo estudios en 1911 del núcleo atómico cargado
positivamente llamando protones a estas partículas, los neutrones
fueron descubiertos en 1932 y se comprobó que no tenían carga
eléctrica.
Es de esperarse que en el presente siglo XXI los avances de la física
sean significativos y se reflejen en avances en la ciencia.

6. ORIGEN Y SIGNIFICADO DE LA FÍSICA.
La palabra física proviene del vocablo griego Physiké que
significa naturaleza y del latín Physis que significa “realidad” o
“naturaleza, en el sentido más amplio.
Ejemplos: La lluvia, la temperatura, la luz del día, la noche, la
gravedad 9.8 m/s2
, las olas del mar, el temblor, el aire, el
movimiento de rotación y traslación.

7. La física es el estudio del universo material, los conceptos básicos
como materia, espacio y tiempo son difíciles de definir de manera
conceptual. La propiedad de la materia es que es observable,
existen conceptos que corresponden a las propiedades básicas de la
materia (como masa, carga, cantidad de movimiento y energía),
otras que describen la ubicación de la materia en el espacio y
tiempo(como el desplazamiento, velocidad y aceleración) o que
pertenecen al comportamiento de la materia en conjunto(calor,
corriente eléctrica, resistencia y presión) todos estos conceptos
tienen significados científicos muy específicos.
INTRODUCCIÓN

8. Las ciencias naturales a diferencia de las ciencias sociales, tiene
a la naturaleza como su objetivo, esto es, a los fenómenos
naturales. La física es la primera ciencia natural, su motivo de
estudio es la composición, estructura, forma, origen, movimiento,
luz y sonido, átomos y moléculas, fisión y fusión, sólidos,
líquidos, gases y en general a todas las cosas físicas. Le
incumbe todo lo que se puede observar y medir.
OBJETIVO

9. CONCEPTO ACTUAL DE LA FÍSICA.
La física actualmente se entiende como la ciencia de la naturaleza
o fenómenos materiales, proviene del griego physis que significa
naturaleza, estudia las propiedades de la materia, la energía, el
tiempo, el espacio y sus interacciones.
La física estudia por lo tanto un amplio rango de campos y
fenómenos naturales, desde las partículas subatómicas hasta la
formación y evolución del universo así como una multitud de
fenómenos naturales que observamos en nuestra vida diaria.

10. DIVISIÓN DE LA FÍSICA.
Para su estudio la Física se divide en:
1.- Física clásica o Newtoniana se funda en tres bases teóricas;
la mecánica newtoniana, la termodinámica y la teoría
electromagnética: Estudia los movimientos que tienen
velocidades pequeñas comparadas con la velocidad de la luz. La
física clásica representa el material conceptual básico que debe
comprenderse para interactuar bien con el ambiente físico a nivel
cotidiano. El principal personaje es Isaac Newton. En esta parte
se estudia la mecánica, óptica, acústica, termodinámica,
electricidad y magnetismo.
2.- Física moderna: se divide en física relativista, que es el
estudio de la teoría de la relatividad y su principal personaje es
Albert Einstein, y en física cuántica que estudia los movimientos
de los átomos y partículas que lo constituyen.

11. MÉTODO CIENTÍFICO EN LA FÍSICA.
Es necesario tener presentes algunos conceptos fundamentales
que nos permitirán entender mejor a la física.
Ciencia. Es un conjunto de conocimientos ordenados y
sistematizados que se refieren a algún hecho o fenómeno
particular.
Teoría. Esquema que se compone como una explicación de un
fenómeno o hecho a partir del cual se fundamenta un conocimiento
o conjunto de conocimientos.
Fenómeno. Cambios espontáneos que suceden en la naturaleza.
Los cambios pueden ser inducidos con el fin de ser estudiados.
Universo. Comprende todo lo que nos interesa e influye en el
comportamiento de los sistemas formados por partículas o cuerpos.

12. Los fenómenos podemos clasificarlos en:
1.- Fenómenos físicos, aquellos que no alteran la estructura
interna de la materia. Por ejemplo el movimiento de los
cuerpos, la luz, etc.
2.- Fenómenos químicos, estos cambios alteran la estructura
interna de la materia. Por ejemplo la combustión de un papel,
la oxidación de un metal, etc.
3.- Fenómenos biológicos, son aquellos que suceden en los
organismos vivientes tales como el nacimiento de una planta,
el desarrollo del cuerpo humano, las enfermedades entre
otras.

13. 1.Microuniverso. Para observarlo nos auxiliamos del
microscopio y podemos ver el comportamiento de pequeñas
partículas.
2. Universo real. Es el que observamos a simple vista y en
donde ocurren los fenómenos que estudiaremos en este curso.
3. Macrouniverso o macrocosmos. Se observa con el
telescopio y se estudia el comportamiento de los astros.
UNIVERSO. Para estudiarlo podemos dividirlo en:

14. MÉTODO CIENTÍFICO.
Es el conjunto de procedimientos que sigue la ciencia para obtener un
conocimiento sobre la naturaleza. Consta de ciertos pasos recomendables,
que permiten al investigador la posibilidad de explicar un fenómeno o suceso.
Los pasos del método científico son:
1. Elección del fenómeno o hecho.
2. Observación. Consiste en fijar la atención de diferentes sentidos para
captar las variables que intervienen en un fenómeno.
3. Razonamiento lógico. Consiste en la construcción de hipótesis y es la
búsqueda de una posible relación causa efecto.
4. Experimentación. Es la repetición sistemática de un hecho o fenómeno,
que nos permite hacer un análisis más amplio de las diferentes variables del
mismo.
5. Obtención de leyes. Son principios que se cumplen cada vez que sucede el
fenómeno en estudio.
6. Verificación y predicción.

15. SISTEMAS DE UNIDADES.
Un sistema es una convención que fija las magnitudes con las
que se van a medir las cantidades físicas que intervienen en un
fenómeno físico, tales como longitud, masa, tiempo, velocidad,
fuerza etc.
Desde su origen el hombre ha tenido la necesidad de medir y
para ello se han establecido unidades patrón. Para construir
los sistemas absolutos de unidades se utilizan las unidades
físicas fundamentales de longitud, masa y tiempo.
En el sistema MKS el metro es la unidad para medir la
longitud, el kilogramo es la unidad para medir la masa y el
segundo para el tiempo.

16. INSTRUMENTOS

17. TABLA DEL SISTEMA ABSOLUTO.
TABLA DEL SISTEMA GRAVITACIONAL.

18. TABLA DE CANTIDADES FUNDAMENTALES DE S.I.

19. CONVERSIÓN DE UNIDADES.
Una aplicación de esto es la conversión de unidades de un
sistema a otro para obtener la equivalencia de una medición en
un fenómeno de un sistema a otro.
Tabla de algunas equivalencias.

20. Ejemplo: Un automóvil viaja a una velocidad de 75 km/h ¿Que
velocidad lleva el automóvil en m/s? ¿Velocidad en ft/s?
Sustituyendo las equivalencias respectivas, se tiene
Ejemplo: Convertir 60 mi/h a pies/s que es la velocidad de un
balón de fútbol americano.

21. ANÁLISIS DIMENSIONAL.
Este análisis consiste en que la unidades de una expresión
matemática o formula se expresen en función de las unidades
fundamentales L, M y T, y se determine que todas las cantidades
sean homogéneas o compatibles.
Ejemplo: ¿Cuales son las dimensiones de la siguiente
ecuación?
Donde

22. Solución: Se sustituyen las dimensiones de cada una de las variables
Simplificando se tiene
Conclusión: como todos los términos tienen las mismas dimensiones
(L) la ecuación es dimensionalmente correcta.

23. ANÁLISIS DE ERRORES.
La física se fundamenta en la determinación cuantitativa de las magnitudes
pertinentes de los fenómenos que estudia, medir implica comparar con una
unidad patrón. Las medidas en ocasiones no permiten obtener el verdadero
valor de las magnitudes que se miden. En algunos aparatos se presentan
imperfecciones y en otras nuestros sentidos cometen equivocaciones. Se tiene
que muchas medidas son inciertas o tienen un cierto grado de incertidumbre.
Al expresar el resultado de una medida pueden especificarse tres elementos:
número, unidad e incertidumbre. Se distinguen dos tipos de errores: errores
sistemáticos y accidentales.
1.Errores sistemáticos. Surgen al emplear un método inadecuado, un
instrumento defectuoso o por usarlo en condiciones imprevistas para su uso.
Al no realizarse las lecturas correctamente o bien al no tener un rango de
precisión adecuado el instrumento de medición.
2.Errores accidentales. Son incertidumbres debidas a numerosas causas
incontrolables e imprevistas que dan lugar a resultados distintos cuando se
repite la medida.

24. El error obtenido en una medición puede expresarse en dos formas:
Error absoluto: es la diferencia del valor obtenido en la medición
menos el valor promedio de las mediciones.
Error relativo: se obtiene dividiendo el error absoluto entre el valor
promedio de las mediciones. Mediante éste se puede saber la calidad
de la medición.
El promedio de los errores con respecto al promedio de las medidas
se representa por la desviación media. Utilizaremos las siguientes
fórmulas:

25. Ejemplo: Los seis integrantes de un equipo de trabajo miden
individualmente la longitud del laboratorio escolar y obtienen los
siguientes datos: 10.57 m, 10.58 m, 10.54 m, 10.53 m, 10.59 m,
10.57 m. Calcular: a) El valor promedio de las mediciones, b) El error
absoluto o desviación absoluta de cada medición, c) La desviación
media o incertidumbre absoluta del valor promedio, d) El error
relativo de cada medición, e) El error porcentual de cada medición.
Solución:

29. NOTACIÓN CIENTÍFICA
La notación científica: sirve para expresar los números de potencia
de 10. el número se expresa como un número comprendido entre
1 y 10 , multiplicado por la potencia de 10 correspondiente.
Repasemos las potencia de 10

30. NOTACIÓN CIENTÍFICA
EjemplosEjemplos
156234000000000000000000000000 ⇒ 1.56234 x 1029
0,0000000000234 ⇒ 2,34 x 10-11
4 x 10 5
= 400 000
3.0 X 10 0
=
6.75 x10 9
=
8.0 x101
=
5680 x 10 5
=
4 x 10 -5
= 0.000 04
6.75 x10-9
=
2.3 x 10-15
=
8.0 x10-1
=
9682.3 x 10-3
=

31. 10= 1x101
4200= 4.2x103
0.00003= 3x10-5
420,000= 4.2x105
25,000= 2.5x104
0.000500= 5.0x10-4
0.000501= 5.01x10-4
= 50.1x10-5
= 501X10-6
NOTACIÓN CIENTÍFICA

32. MULTIPLICACIÓN DE POTENCIA DE 10

34. SISTEMAS DE REFERENCIA.
En mecánica se tratan problemas relacionados con la descripción del
movimiento de un objeto en el espacio, por lo que se requiere un
método para conocer la posición de ese objeto. Para esto se definen los
sistemas de coordenadas y marcos de referencia. Un sistema de
coordenadas usado para indicar las posiciones en el espacio consta de:
1. Un punto de referencia fijo O,
llamado origen.
2. Un conjunto de ejes o
direcciones con una escala
apropiada.
3. Instrucciones sobre como
identificar un punto en el
espacio respecto al origen y a
los ejes.

35. SISTEMAS DE REFERENCIAS
Un sistema de referencia (o marco de referencia) es un conjunto
de convenciones usadas por un observador para poder medir la
posición y otras magnitudes físicas de un sistema físico y de
mecánica.
Para nuestra información o
para cualquier persona la
posición de un punto en el
plano cartesiano, lo podemos
denotar por:
Por ejemplo el punto B en el
grafico se encuentra ubicado
en las coordenadas (6 en x , 5
en y) ó (6, 5).
Coordenadas Cartesianas
o
rectangular (x, y)

36. MOVIMIENTO EN UN PLANO
• El estudio de la Física va de lo sencillo a lo complejo y de lo
particular a lo general.
• En este contexto, se analiza el movimiento de un cuerpo que
se mueve ya no en un eje (recta), sino en dos ejes
mutuamente perpendiculares que forman una superficie.
• Estos ejes serán ahora nuestro sistema de referencia, al cual
también se le conoce como:

37. SISTEMA DE COORDENADAS CARTESIANO O COORDENADAS
RECTANGULARES
y + ( unidades)
eje vertical
(variable dependiente)
x + (unidades)
eje horizontal
(variable independiente)
0 1 2 3 4
1
2
-1
-2
-3
-1-2-3-4
l l l l l
lll
l l l l l
llll
3
abscisas
ordenadas

38. LOCALIZACIÓN DE UN PUNTO EN EL PLANO
CARTESIANO
• Se hace a partir del origen del sistema, ya sea
• Mediante la pareja de puntos coordenados (x,y
• Especificando la distancia, el ángulo y a partir de que eje y hacia
donde se mide el ángulo.
θ
y + (m)
x + (m)0 1 2 3 4
1
2
-1
-1-2-3-4
3 (4,3)
d
I cuadranteII cuadrante
III cuadrante IV cuadrante- 2
l l l l l l l l l l

39. Como medir DISTANCIAS EN EL PLANO
(Teorema de Pitágoras)
( ) ( )2
12
2
12 yyxxd −+−=
( ) ( ) mmmmmmmmd 5259160304 22222
==+=−+−=
θ
y + (m)
x + (m)0 1 2 3 4
1
2
-1
-1-2-3-4
3
( 4 , 3 )
d
- 2
l l l l l l l l l l l
(x 2 , y 2)
(x 1 , y 1)
( 0 , 0 )
x 2 - x 1
y 2 - y 1
P1(x1,y1)= (0,0)
P2(x2,y2)= (4,3)

40. Como medir el ANGULO
Se forma un triángulo rectángulo, donde el lado más largo se denomina
hipotenusa y los lados más cortos catetos.
– El lado que está junto al ángulo se denomina cateto adyacente
– El cateto opuesto es el que se encuentra en el lado contrario al
ángulo.
θ
y + (m)
x + (m)
0 1 2 3 4
1
2
-1
-1-2-3-4
3
(4,3)
Cateto opuesto
Hipotenusa
Cateto adyacente
- 2
•Se requiere conocer las funciones trigonométricas

41. FUNCIONES TRIGONOMÉTRICAS
d
yy
hipotenusa
opuestocateto
sen 12 −
==θ
d
xx
hipotenusa
adyacentecateto 12
cos
−
==θ
12
12
tan
xx
yy
adyacentecateto
opuestocateto
−
−
==θ
θ
y + (m)
x + (m)
0 1 2 3 4
1
2
-1
-1-2-3-4
3
(4,3)
Cateto opuesto
Hipotenusa
Cateto adyacente
- 2

42. • El ángulo se encuentra sacando el inverso de la función seleccionada
• El sentido se estipula haciendo referencia a los puntos cardinales. El
ángulo anterior se expresa en función de dichos puntos como:
• Lo cual indica que el ángulo se está midiendo hacia el Norte a partir
del Este.
EdelNal0
87.36
0111121
87.36)6.0(
5
3
5
03
==





=




 −
=




 −
= −−−−
sen
m
m
sen
m
mm
sen
d
yy
senθ

43. • Un cuerpo cambia de posición, si cambia una de las parejas
coordenadas (x , y)
• Eso implica que hay desplazamiento.
• Este se calcula de la forma acostumbrada
Posición final – Posición inicial
• Como involucra dos variables (x , y) se utiliza el teorema de
Pitágoras para determinar la magnitud del desplazamiento (que en
la mayoría de las situaciones, no es igual a la distancia recorrida).
• Veámoslo mediante un ejemplo que involucra dos movimientos
sucesivos.
CAMBIO DE POSICIÓN EN EL PLANOCAMBIO DE POSICIÓN EN EL PLANO

44. • Un cuerpo inicialmente se encuentra en el origen. Recorre 4 m en
dirección horizontal en el sentido del eje de las x positivo.
Posteriormente se mueve 3 m en dirección vertical en sentido del
eje y positivo.
• Los cambios de posición se representan gráficamente en el plano
cartesiano mediante flechas A y B.
• La longitud de las flechas es proporcional a la distancia que recorre.
• La punta de la flecha indica el sentido en el cual a ocurrido el
movimiento.
Ejemplo CAMBIO DE POSICIÓN EN EL PLANO

45. Representación gráfica deRepresentación gráfica de
CAMBIO DE POSICIÓN EN EL PLANOCAMBIO DE POSICIÓN EN EL PLANO

46. • El DESPLAZAMIENTODESPLAZAMIENTO resultante o cambio de posición se representa
mediante la flecha C que va desde la posición inicial hasta la posición final.
Tiene las siguientes características:
Magnitud (o longitud): 5
Unidad: metros
Dirección: 36.87 0
Sentido: al Norte del Este
Todas las cantidades físicas que cumplan con las características anteriores,
se les denominan VECTORES .
VectorVector DESPLAZAMIENTODESPLAZAMIENTO
y + (m)
x + (m)
0 1 2 3 4
1
2
-1
-1-2-3-4
3
(4,3)
- 2
C
Posición inicial
Posición final
N
S
O E

47. ESCALARES
• Son todas aquellas cantidades físicas que para especificarse
completamente basta con dar un número y su unidad
correspondiente.
• Se manejan mediante las operaciones ordinarias de la
aritmética: suma, resta, multiplicación y división.
Cantidad físicaCantidad física UnidadesUnidades Cantidad físicaCantidad física UnidadesUnidades
TiempoTiempo 30 s30 s VolumenVolumen 10 cm10 cm33
MasaMasa 20 kg20 kg GravedadGravedad 9.81 m/s9.81 m/s22
Distancia, longitud,Distancia, longitud,
profundidad, altura.profundidad, altura.
50 m50 m PresiónPresión 760760
mmHgmmHg
TemperaturaTemperatura 303000
CC DensidadDensidad 1 Kg/m1 Kg/m33
RapidezRapidez m/sm/s CargaCarga 5x105x10-6-6
CoulombCoulomb

48. VECTORES
Son todas aquellas cantidades físicas que para especificarse
completamente hay que proporcionar:
– un número (4);
– una unidad (m, m/s, Newton, Newton / Coulomb);
– una dirección (horizontal, vertical, inclinada);
– un sentido (derecha, izquierda, arriba, abajo, eje x positivo, eje x
negativo)
Se representan gráficamente mediante flechas.
•Se manejan mediante operaciones especiales:
– Suma y resta vectorial
– Producto punto o producto escalar
– Producto cruz o producto vectorial

49. CANTIDADES VECTORIALES
CantidadCantidad MagnitudMagnitud UnidadUnidad DirecciónDirección SentidoSentido
DesplazamientoDesplazamiento
55 mm HorizontalHorizontal Hacia la izquierdaHacia la izquierda
FuerzaFuerza 1010 NewtonNewton 303000
al N del Eal N del E
PesoPeso
1515 NewtonNewton VerticalVertical Hacia el centro deHacia el centro de
la Tierrala Tierra
AceleraciónAceleración
9.819.81 m/sm/s22
VerticalVertical Hacia el centro deHacia el centro de
la Tierrala Tierra
Campo EléctricoCampo Eléctrico
1212 N/CN/C RadialRadial SaliendoSaliendo
VelocidadVelocidad
1111 Km/hrKm/hr 606000
A partir del eje xA partir del eje x++
en sentido de lasen sentido de las
manecillas delmanecillas del
relojreloj
Graficar los vectores anteriores en el plano cartesianoGraficar los vectores anteriores en el plano cartesiano

50. Diferencia entre escalares y vectores
Para diferenciar entre escalares y vectores analicemos los siguientes
ejemplos:
La distancia entre dos puntos es de 5 metros (es un escalar).
Una persona recorre 5 metros de donde estaba inicialmente.
(hay un cambio de posición o desplazamiento)
5 es el NÚMERO de metros y éste a su vez es la UNIDAD. Sin embargo
no podemos localizar a la persona, puede estar ubicada en cualquier
punto deuna circunferencia de radio 5 metros, medidos a partir de donde
estaba inicialmente. Tenemos que dar su DIRECCIÓN y SENTIDO, por
ejemplo 300
al S del O

51. PROPIEDADES DE LOS
VECTORES

52. Todo vector se puede desplazar por el espacio si se mantiene la
magnitud, dirección y sentido
A
 B

C

A B C= =
 

53. A
Sea el vector A
B = λ AEl resultado es otro vector en la misma dirección
Si multiplicamos un escalar “ λ ” y un vector “A”
λ > 0
Para: λ > 0 , el vector B es
paralelo al vector A
B

54. A
Sea el vector A
B = λ AEl resultado es otro vector en la misma dirección
Si multiplicamos un escalar “ λ ” y un vector “A”
Para: λ < 0 , el vector B es
anti paralelo al vector A
B

55. A

B

AB

2
1
=
A

B

AB

4
1
−=

56. COLINEALES.- Cuando las líneas de acción son paralelas.
A
B
C

57. A
Sea el vector A
B = λ AEl resultado es otro vector en la misma dirección
Si multiplicamos un escalar “ λ ” y un vector “A”
Para: λ = 1 , el vector B es
igual al vector A
B
λ = 1

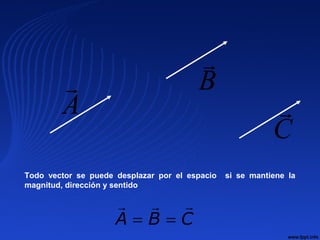
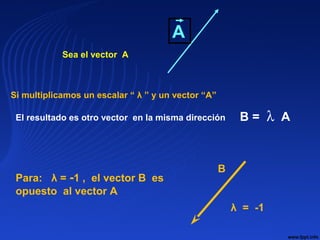
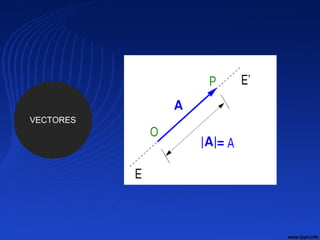
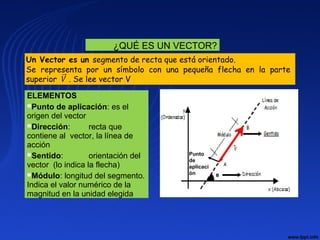
58. VECTORES IGUALES.- Si tienen su módulo, dirección
y sentido iguales
α β
A B
Si A y B son iguales se cumple
[ A] = [ B]
α = β
Sentido de A = Sentido de B

59. A
Sea el vector A
B = λ AEl resultado es otro vector en la misma dirección
Si multiplicamos un escalar “ λ ” y un vector “A”
Para: λ = -1 , el vector B es
opuesto al vector A
B
λ = -1

60. COLINEALES.- Si se encuentran sobre la misma línea de
acción.
CONCURRENTES.- Si sus líneas de acción concurren en un mismo
punto.
A
C
B
Punto de
Concurrencia
A B C

61. SUMA y RESTA de
VECTORES

62. El vector que empieza en el origen de uno de los vectores y termina en el final
de el otro vector es el vector suma R
B
A
Si deseamos sumar dos vectores, se coloca un vector a continuación
del otro vector
RA
B
R B
A

63. 2AB.cosθ
2
B
2
AR ++=
θ
A
B
R

64. Si los vectores son perpendiculares
22
BAR +=
B
A
R

65. rβ
α
R
B
A
Ley de SenosLey de Senos

66. Suma de n VectoresSuma de n Vectores
B
A C

67. PropiedadesPropiedades
de la suma dede la suma de
VectoresVectores
Ley Conmutativa
ABBAR +=+=
Ley Asociativa
C)BA)CBAR

++=++= ((

68. Resta deResta de
VectoresVectores R A (-B)= +
  
A
B A
-B
R

69. A
B
R=A+B
A
B
R=A-B

70. COMPONENTES DE UN VECTOR

71. COMPONENTES DE UN VECTOR
A
u
A
u
A
u
A
u
Un vector tiene muchas componentes , un caso particular
son las componentes rectangulares

72. y
x
A
u
Ax
Ay

yA
u
xA
u
x
y
A Acos
A A sen
= θ
= θ
COMPONENTES RECTANGULARES EN EL
PLANO
AX , AY : proyecciones o componentes
AX , AY : vectores componentes A = AX + AY

73. AZ
Ax
COMPONENTES RECTANGULARES EN EL
ESPACIO
A = Ax + Ay + Az

74. VECTORES UNITARIOS

75. Vector Unitarios
• Un vector cuya magnitud es la unidad y
es paralelo al vector, se denomina vector
unitario.
$ A
A
u =
A
u u
A
u

76. Vectores unitarios en el plano cartesiano
iˆjˆ
x
y
iˆ Vector unitario en la dirección del eje x+
jˆ Vector unitario en la dirección del eje y+

77. Vectores unitarios en el espacio
x
iˆ
z
kˆ
yjˆ

78. Representación deRepresentación de
un vector conun vector con
vectores unitariosvectores unitarios
x
y
z
θ
ϕ
A
Ax
Ay
Az
2 2 2
x y zA A A A A= = + +

kAjAiAA zyx

++=x y z
A A i A j A k= + +


79. OPERACIONES ANALÍTICAS CON
VECTORES

80. Y
X
SUMA ANALÍTICA DE VECTORES
→
R
A
→
∧
j ∧
i
AX
AY
B
→
BX
BY
X YA = A i + A j
u
$ $
X YB = B i + B j
u
$ $
( ) ( ) ( ) ( )  = + +   
u  uu
x yAR = + +A AB x y jBi jBi

81. PRODUCTO ESCALAR

82. x x y y z z
A B ABcos( )
A B A B A B A B
→ →
→ →
• = θ
• = + +
ProductoProducto
escalar de dosescalar de dos
vectoresvectores
A
B
θ

83. ProductoProducto
escalar de dosescalar de dos
vectoresvectores
θABBA cos=⋅

cosθAAB
=
Proyección de A sobre B
cosθBBA =
Proyección de B sobre A
ProductoProducto
escalar de dosescalar de dos
vectoresvectores

84. Propiedades del producto escalar
Teorema: Sean a,b vectores en ℜ2
y α un
número real, entonces:
 a.0 = 0
 a.b = b.a (propiedad conmutativa)
 (αa).b = α(a.b) = a.(α b)
 a.(b + c) = a.b + a.c (propiedad distributiva)
Si a . b = 0 entonces el vector a es
perpendicular al vector b
2
.a a a=

85. 1ˆˆ =⋅ii
1ˆˆ =⋅ jj
0ˆˆ =⋅ ji
0ˆˆ =⋅kj
0ˆˆ =⋅ki
xAiA =⋅ ˆ

1ˆˆ =⋅kk
yAjA =⋅ ˆ

zAkA =⋅ ˆ
 X X Y Y Z ZA B A B A B A B⋅ = + +
 

86. PRODUCTO VECTORIAL

87. ProductoProducto
vectorial de dosvectorial de dos
vectoresvectores
BAC

×=
A x B = |A| |B| sen φ û

88. Producto Vectorial: AxB
A x B = |A| |B| sen φ û A x B = - B x A

89. 0iˆiˆ

=× 0ˆˆ

=× jj
0ˆˆ

=× kk
kji ˆˆˆ =× ikj ˆˆˆ =×
jik ˆˆˆ =×
PRODUCTO VECTORIAL DE LOS VECTORES UNITARIOS

90. NOTACIÓN DE VECTORES
• Se denotan (escriben) mediante letras mayúsculas o minúsculas, a
las cuales se les pone encima una flechita para indicar que es un
vector. Ejemplo:
• Generalmente en libros de textos o notas de clase donde se facilita
más la escritura, se suprime la flechita pero se remarca la letra por
ejemplo:
A, B, C, D, E, etc. ó a, b, c, etc.
que comúnmente son llamadas "negritas"
.. etcetc dcbaFCBA
→→→→→→→→

91. Representación, magnitud e igualdad de Vectores
• Se representan mediante flechas.
A b
F c
 Su magnitud es proporcional a la longitud de la flechaSu magnitud es proporcional a la longitud de la flecha
A Magnitud del vector A = valor absoluto del vector A
A = |A| = |A|
 Dos o más vectores son iguales si tienen la misma magnitud, dirección y sentido, no importa si sus orígenes noDos o más vectores son iguales si tienen la misma magnitud, dirección y sentido, no importa si sus orígenes no
coincidancoincidan..
A
B
F c
A = B = c ≠ F ≠ M
M

92. OPERACIONES CON VECTORES
Como se mencionó anteriormente, los vectores se manejan mediante
operaciones especiales siendo éstas:
• SUMA VECTORIAL.- Sean A y B dos vectores, se define la suma
vectorial como:
A + B = C
donde C es un nuevo vector con su propia magnitud, dirección y sentido.
• PRODUCTO ESCALAR O PRODUCTO PUNTO.- Sean A y B dos
vectores, se define el producto punto entre los dos vectores como:
A ● B = |A| |B| cos θ = A B cos θ = B A cos θ = C
donde A B cos θ = C es un escalar que posee únicamente
magnitud y unidad.
θ es el MENOR ÁNGULO que se forma entre los dos vectores. Si ….

93. OPERACIONES CON VECTORES …
00
< θ < 900
A ● B > 0
θ = 900
A ● B = 0
900
< θ < 2700
A ● B < 0
θ = 2700
A ● B = 0
2700
< θ < 3600
A ● B > 0

94. OPERACIONES CON VECTORES
• PRODUCTO VECTORIAL O PRODUCTO CRUZ
Sean A y B dos vectores, se define el producto vectorial como:
dondedonde CC es un nuevo vectores un nuevo vector
 LaLa MAGNITUDMAGNITUD del vectordel vector CC viene dada por:viene dada por:
A x B = C
|C| = C = | A x B | = | A | | B | sen θ = AB sen θAB
Donde θAB es el menor ángulo que se forma entre los vectores
 LaLa DIRECCIÓNDIRECCIÓN del vectordel vector CC es perpendicular tanto al vectores perpendicular tanto al vector AA
como alcomo al BB
 SuSu SENTIDOSENTIDO viene dado por laviene dado por la REGLA DE LA MANO DERECHAREGLA DE LA MANO DERECHA

95. Regla de la mano derecha
• Con los dedos extendidos de la mano derecha y el pulgar perpendicular
a ellos, tratar de empujar la punta del primer vector hacia la punta del
segundo vector cerrando los dedos y dejando extendido el pulgar, el
sentido en el que apunta este pulgar, nos indicará el sentido hacia
donde apunta el vector C o producto vectorial entre los dos vectores
A
B
θ
C = A x B
A
B
θ
C' = B x AA x B = - B x A
Si el ángulo entre los dos vectores es de 90Si el ángulo entre los dos vectores es de 9000
, entonces el producto vectorial entre, entonces el producto vectorial entre
ellos es el VECTOR NULO o Vector cero, ya que Sen 90ellos es el VECTOR NULO o Vector cero, ya que Sen 9000
= 0= 0
NotaNota: Los vectores: Los vectores AA yy BB forman o están en un plano, siendo el vectorforman o están en un plano, siendo el vector CC
perpendicular a dicho plano, por ejemplo, es como si los vectoresperpendicular a dicho plano, por ejemplo, es como si los vectores AA yy BB estuviesenestuviesen
en el piso, luego entonces, el vectoren el piso, luego entonces, el vector CC estaría saliendo o entrandoestaría saliendo o entrando
perpendicularmente al piso.perpendicularmente al piso.

96. Para sumar dos o más vectores,
existen dos métodos:
• Métodos Gráficos
– Método del paralelogramo (es
ideal para dos vectores)
– Método del polígono ( Para sumar
más de dos vectores)
• Método Analítico
Suma de V e c t o r e s

97. Consiste en sumar dos vectores
gráficamente y se realiza de la
siguiente manera:
• Se unen los orígenes de los
dos vectores.
• A partir de sus puntas o
terminaciones se trazan
paralelas a cada uno de ellos
formando una paralelogramo.
• La diagonal de dicho
Método del Paralelogramo

98. ejemplo:
Método del ParalelogramoMétodo del Paralelogramo
A
B
A
B
Resultante

99. Consiste en unir el origen del segundo vector con la punta
del primero. Si son mas de dos vectores, unir el origen
del tercer vector con la punta del segundo y así
sucesivamente, el vector resultante es el que va desde
el origen del primero hasta la punta del último.
A
B
B
Resultante
C
A
C
D
D
Método del Polígono

100. Ley conmutativa de la suma:
• Al sumar dos o mas vectores se obtiene el mismo
resultado, no importa el orden en que se sumen. Del
ejemplo anterior:
A
B
C
D
BA
C
D
Resultante
Resultante
C
D
A
B
Propiedades de la Suma Vectorial

101. Ley asociativa de la suma:
• Al sumar dos o mas vectores, algunos o todos se
pueden asociar para obtener semi-resultantes, las
cuales se suman a su vez para obtener el vector
resultante. Del ejemplo anterior:
Propiedades de la Suma VectorialPropiedades de la Suma Vectorial
A
B
B
Resultante
C
A
C
D
D
A +
D
C + B

102. Multiplicación de un vector por
un escalar
• Al multiplicar un vector por un escalar, se obtiene
un nuevo vector ( B ) que es k veces mayor, k veces
menor o bien igual que el vector que le dio origen,
todo depende del escalar. Ejemplo:
Propiedades de la Suma VectorialPropiedades de la Suma Vectorial
F
B = 2 F
k = 2
k = 1/2
W = 1/2 F = F/
2

103. Negativo de un vector
• El negativo de un vector S es aquél que tiene la
misma magnitud y dirección que S pero sentido
contrario.
• El negativo de un vector S es aquél que hay que
sumarle a S para obtener el vector nulo.
• O bien el vector multiplicado por un escalar unitario
negativo. Ejemplo:
Propiedades de la Suma VectorialPropiedades de la Suma Vectorial
S
-
S
B = - S
k = - 1
S + ( - S ) =
0

104. Se define la resta de vectores como:
A - B = A + ( - B ) = R
Para restar un vector B al vector A, se procede igual que
en la suma con la única salvedad de que se toma el
negativo del vector B. Ejemplo
A
B
A
+ ( - B ) = R
A
- B
Resta de Vectores

105. Se define la resta de vectores como:
A - B = A + ( - B ) = R
Para restar un vector B al vector A, se procede igual que
en la suma con la única salvedad de que se toma el
negativo del vector B. Ejemplo
Resta de Vectores …Resta de Vectores …
A
B A
– B = A
+ ( - B ) = R
A
- B
B – A
= - (A
- B ) = - R
- A
B

106. • El método analítico consiste en hablar de vectores con
respecto a un sistema de referencia, en el caso del
plano, éste es el plano cartesiano
M E T O D O A N A L Í T I C OM E T O D O A N A L Í T I C O
A
0 1 2 3 4
1
2
-1
-2
-3
-1-2-3-4
l l l l l
lll
l l l l l
llll
3
x +
y +

107. • Una vez elegido el plano, se definen las componentes
Ax y Ay de un vector como las proyecciones o sombras
del vector sobre los ejes coordenados, éstas se
obtienen trazando paralelas a los ejes a partir de la
terminación del vector.
Método analítico:Método analítico: componentes rectangularescomponentes rectangulares
A
0 1 2 3 4
1
2
-1
-2
-3
-1-2-3-4
l l l l l
lll
l l l l l
llll
3
x +
y +
A x
A y

108. • Cuando se proporciona la magnitud del vector y su orientación
mediante el ángulo, las componentes rectangulares se calculan
utilizando las funciones trigonométricas.
• Se forma un triángulo rectángulo, en donde las componentes vienen
siendo los catetos y la hipotenusa la magnitud del vector. Aplicando
las funciones trigonométricas:
Método analítico:Método analítico: cálculo de las componentes rectangularescálculo de las componentes rectangulares
A y
A
0 1 4
1
-1
-1
ll
l l l
3
x +
y +
A x
θ
cateto adyacente
cateto opuestohipotenusa
hipotenusa
cateto opuesto
sen θ = =
A y
|A|
despejando la componentedespejando la componente
vertical:vertical:
despejando la componente horizontal:despejando la componente horizontal: A x= |A| cos θ
cos θ =
hipotenusa
cateto Adyacente
=
A x
|A|
A y = |A| sen θ

109. • Cuando se proporcionan las componentes rectangulares (A x , A y ) de
un vector, se puede conocer:
– Su magnitud aplicando el teorema de Pitágoras
– Su orientación mediante el inverso de la función tangente del ángulo.
A y
A
0 1 4
1
-1
-1
ll
l l l
3
x +
y +
A x
hipotenusa
θ
|A| = √ (A x )2
+ ( A y )2
θ = tan -1
A y
A x
tan θ = cateto opuesto
cateto adyacente
A y
A x
=
Método analítico: cálculo de la magnitud y ángulo de un
vector

110. Cuando se proporcionan las componentes rectangulares (A x , A y ) de un
vector, éste puede estar en:
• I cuadrante si: Ax > 0 y Ay > 0 sentido al N del E
• II cuadrante si: Ax < 0 y Ay > 0 sentido al N del O
• III cuadrante si: Ax < 0 y Ay < 0 sentido al S del O
• IV cuadrante si: Ax > 0 y Ay < 0 sentido al S del E
Método analítico:Método analítico: ubicación y orientación de un vectorubicación y orientación de un vector
x +
A y
A
0 1 4
1
-1
-1
ll
l l l
3
x +
y +
A x
A y < 0
A
y +
A x < 0
θ
N
S
O E
Aplicando la igualdad de
vectores

111. Método analítico:Método analítico: problema de la tangenteproblema de la tangente
si:si: || AxAx || >> || AyAy || mas orientado al eje Xmas orientado al eje X
si:si: || AyAy || >> || AxAx || mas orientado al eje Ymas orientado al eje Y
A y > 0
A
0
4
-1
-1
l
l l
2
x +
y +
A x > 0
θ
A x y A y > 0
O
x +
A y < 0
A
y +
A x < 0
θ
N
S
E
A x y A y < 0
En ambos casos la función tan θ es positiva.
Se recomienda graficarlos para visualizarlos o, analizar signos
para ubicarlos en el cuadrante respectivo. Su orientación será
de acuerdo a:
-4
-2

112. A
0
4
-1
-1
l
l l
2
x +
y +
θ
Método analítico: problema del ángulo y los
ejes
• El ángulo puede ser dado respecto al eje x o con respecto al eje y. Hay que
tener cuidado al aplicar las funciones trigonométricas para calcular las
componentes, ya que para la misma función, las componentes CAMBIAN.
A
0
4
-1
-1
l
l l
2
x +
y +
θ
hip.
cat. op.
sen θ = =
A y
|A|
A y = |A| sen
θ
A x = |A| cos
θ
hip.
cat. op.
sen θ = =
A x
|A|
A y = |A| cos
θ
A x = |A| sen θ

113. Suma de vectores: método analítico
A
B
R
θR
θB
θA
A x B x
R x
A y
B y
R y
x +
y +
| R |= √ ( Rx)2
+ (Ry)2
Donde:
Rx= Ax + Bx
Ry= Ay + By
Además:
Ax = | A | cos θA
Ay = | A | sen θA
Bx = | B | cos θB
By = | B | sen θB
θR= tan -1 Ry
Rx

114. Ejercicio: suma de vectores
La magnitud del vector A es de 200 unidades y forma una
ángulo de 300
con respecto a la horizontal; la magnitud del
vector B es de 300 unidades y forma una ángulo de 1350
con
respecto a la horizontal; la magnitud del vector C es de 150
unidades y forma un ángulo de 2350
con respecto a la
horizontal. Todos los ángulos son medidos en sentido
contrario a las manecillas del reloj.
a) Utilizando el método gráfico,
encuentre:
i ) A + B + C
ii ) B + A + C
iii ) A - B + C
iv ) C - B – A

115. Representación de vectores: vectores unitarios
Para representar un vector en forma vectorial, lo analizaremos mediante los
siguientes ejemplos:
A = |A|
Simbología incorrecta, ya que un vector no puede ser igual a un escalar como lo es la
magnitud de un vector.
A = A x + A y
Simbología incorrecta, ya que un vector no puede ser igual a la suma de dos escalares
como lo son las componentes rectangulares de un vector.
|A| = A x + A y
Simbología incorrecta, ya que la magnitud de un vector se determina mediante el
teorema de Pitágoras.
Como se puede apreciar, aún no contamos con una terminología para describir a un
vector en notación vectorial.
Para suplir esta falta de información, se definen los vectores unitarios î , ĵ cuya
magnitud como su propio nombre lo indica es la unidad y su dirección es a lo largo de
los ejes coordenados, su sentido saliendo del origen.
Veámoslos en el plano.

116. Vectores unitarios
Para indicar que se trata de un vector unitario, encima de la letra se le
pone un gorrito.
La letra î se reserva para el vector unitario en la dirección del eje de
las x positivo
La letra ĵ para el vector unitario en la dirección del eje de las y
positivo.
También pueden ser escritos en negritas.
Se le conocen también como vectores direccionales
î = i
ĵ = j
| î |
= | ĵ | = 1
1 2
1
2
î
ĵ
x +
y +
Un vector se representa como:
A = Ax i + Ay j

117. Suma de Vectores: método de vectores unitarios
Sumar los siguientes vectores:
A = 4 i + 5 j
B = 6 i + 2 j
Solución
C = A + B = (4 i + 5 j ) + (6 i + 2 j )
= 4 i + 6 i + 5 j + 2 j
= (4 + 6) i + (5 + 2) j
=10 i + 7 j
ó más sencillo
A = 4 i + 5 j +
B = 6 i + 2 j
R = 10 i + 7 j
R = |R| = √100+49 = √149 = 12.2 u
θ = tan-1
(7/10) = 350
Como Rx y Ry son positivos, el vector resultante se encuentra en el I cuadrante; como Rx > Ry, mas cargado hacia el eje x. Es decir, al N del E
5 10
5
10
x +
y +
Dibujar los vectores y sumarlos

118. Producto punto o producto escalar
El producto punto o producto escalar se definió como:
A ● B = |A| |B| cos θ = A B cos θ
En función de los vectores unitarios
A ● B = (A x i + A y j) ● (B x i + B y j)
Desarrollando:
A●B = A x B x (i●i) + A x B y (i●j) + A y B x (j●i) + A y B y (j●j)
Aplicando la definición
i ● i = (1) (1) cos 00
= 1
i ● j = (1) (1) cos 900
= 0
j ● j = (1) (1) cos 00
= 1
j ● i = (1) (1) cos 900
= 0

119. Producto punto …
Sustituyendo los productos punto
A ● B = A x B x + A y B y
Igualando ambas definiciones
|A| |B| cos θ = A x B x + A y B y
Despejando el ángulo
θ = cos-1
A x B x + A y B y
||AA| || |BB||

120. Ejemplo: producto punto
Encontrar el producto punto o producto escalar de los siguientes
vectores:
A = 4 i + 5 j análisis: I cuadrante a 51.340
al N del E; magnitud 6.4
B = 6 i + 2 j análisis: I cuadrante a 17.430
al N del E; magnitud 6.3
A ● B = A x B x + A y B y
= 24 + 10
= 34
El menor ángulo que forman entre si los dos vectores es:
θ = cos-1
θ = cos-1
θ = 32.90
A x B x + A y B y
||AA| || |BB||
34
√16+25 √36+4

121. Producto cruz o producto vectorial
El producto cruz o producto vectorial se definió como:
A x B = |A| |B| sen θ = A B sen θ
En función de los vectores unitarios
A x B = (A x i + A y j) x (B x i + B y j)
Desarrollando:
AxB = A x B x (ixi) + A x B y (ixj) + A y B x (jxi) + A y B y (jxj)
Aplicando la definición
i x i = (1) (1) sen 00
= 0
i x j = (1) (1) sen 900
= k (aplicando la regla de la mano derecha)
j x j = (1) (1) sen 00
= 0
j x i = (1) (1) sen 900
= -k (aplicando la regla de la mano derecha)

122. Producto cruz …
Sustituyendo los productos cruz de vectores unitarios
A x B = A x B y (k) + A y B x (-k)
A x B = (A x B y - A y B x ) k
Un nuevo vector cuya:
Magnitud es: A x B y - A y B x
Dirección: perpendicular al plano formado por A y B.
Sentido:
Sale del plano si A x B y - A y B x > 0
Entra al plano si A x B y - A y B x > 0

123. Producto cruz en tres dimensiones
El producto cruz o producto vectorial de vectores unitarios
A x B = (A x i + A y j + A z k) x (B x i + B y j + B z k)
Desarrollando:
A x B = A x B x (i x i) + A x B y (i x j) + A x B z (i x k) +A y B x (j x i) + A y B y (j x
j) + A y B z (j x k) + A z B x (k x i) + A z B y (k x j) + A z B z (k x k)
Aplicando la definición
i x i = (1) (1) sen 00
= 0
i x j = (1) (1) sen 900
= k
i x k = (1) (1) sen 900
= - j
j x i = (1) (1) sen 00
= - k
j x j = (1) (1) sen 900
= 0
j x k = (1) (1) sen 900
= i
k x i = (1) (1) sen 00
= j
k x j = (1) (1) sen 900
= - i
k x k = (1) (1) sen 900
= 0

124. Producto cruz …
Sustituyendo
A x B = AxBy (k) + AxBz (-j) +AyBx (-k) + AyBz (i) + AzBx (j) + AzBy (-i)
Reagrupando
A x B = (AyBz - AzBy) i + (AzBx - AxBz) j + (AxBy - AyBx) k

125. Producto cruz: determinantes
A x B =
i j k
Ax Ay Az
Bx By Bz
= +(Ay Bz - By Az ) i - (Ax Bz - Bx
Az ) j
+ (Ax By – Bx Ay )k

126. VECTORES

127. ELEMENTOS
Punto de aplicación: es el
origen del vector
Dirección: recta que
contiene al vector, la línea de
acción
Sentido: orientación del
vector (lo indica la flecha)
Módulo: longitud del segmento.
Indica el valor numérico de la
magnitud en la unidad elegida
¿QUÉ ES UN VECTOR?
Un Vector es un segmento de recta que está orientado.
Se representa por un símbolo con una pequeña flecha en la parte
superior . Se lee vector V
Punto
de
aplicaci
ón