El documento presenta información sobre las emisiones de gases de efecto invernadero en Chile en 2016. Se emitieron 13 959 687 500 kg de dióxido de carbono y 2 215 823 412 kg de metano. Se pide calcular la diferencia entre las emisiones de estos gases y el total emitido.










































![45
Lección 4 • Razones y porcentajes
6. Propón 2 razones para cada imagen y explícalas.
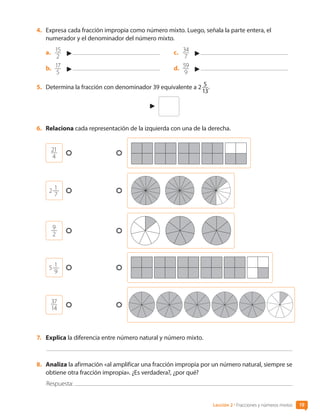
a. b.
Razón 1
Razón 2
Razón 1
Razón 2
7. Analiza los conjuntos de piezas de ajedrez.
Conjunto 2
Conjunto 1
a. ¿En qué conjunto es mayor la razón de la cantidad de piezas blancas respecto del total?
Respuesta:
b. ¿En cuál es menor la razón de la cantidad de piezas negras respecto del total?
Respuesta:
c. ¿Qué pieza trasladarías de un conjunto a otro de manera que la razón de la cantidad de piezas
blancas respecto del total sea la misma en ambos conjuntos? [Profundización]
Respuesta:
CL0000000001374 MATE_6B_CA_U1B_7104.indd 45 11-12-20 16:06](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-47-320.jpg)


















![Lenguaje algebraico
1. Describe qué es el lenguaje algebraico y da un ejemplo.
2. Expresa con lenguaje algebraico.
a. Un número aumentado en 20.
b. Un número multiplicado por 2 y dividido por 5.
c. Un número disminuido en su cuarta parte.
d. Un número multiplicado por sí mismo.
e. Un número triplicado y luego disminuido en 7.
f. La octava parte de un número aumentada en 1.
3. Expresa con lenguaje cotidiano.
a. x + 11
b. 18 – x
c. 2x – 4
d. 12 – 3x
e. ]x + 3g • 2
f. 4x + 3x + 2x – 1
Unidad 2 • La tecnología
64
CL0000000001374 MATE_6B_CA_U2_7150.indd 64 11-12-20 16:07](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-66-320.jpg)
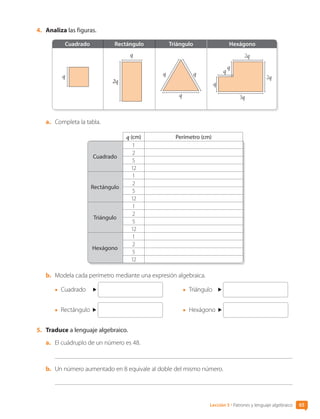

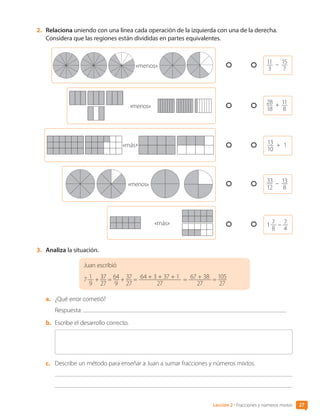
![7. Dos integrantes. Analicen el rectángulo.
Etapa 1 (grupal): Construyan una tabla de valores naturales para
p y q.
Rectángulo A B C D E F G
p (cm)
q (cm)
Etapa 2 (individual): Calcula el área del rectángulo usando una de las multiplicaciones: p • q o q • p.
Rectángulo A B C D E F G
Área (cm2
)
Etapa 3 (grupal): Comparen los valores de área obtenidos de esta manera. Relaciónenlos con la
propiedad conmutativa de la multiplicación y redacten una conclusión. [Profundización]
Conclusión:
8. Traduce a lenguaje cotidiano de acuerdo con la situación del problema .
En las imágenes, el precio de venta de dos equipos se representa con letras.
$D
$E
a. D + E
b. 2 • E
c. 2 • D = E
d.
E
2
= D
p
q
Lección 5 • Patrones y lenguaje algebraico 67
CL0000000001374 MATE_6B_CA_U2_7150.indd 67 11-12-20 16:07](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-69-320.jpg)
![9. Inventa una situación cotidiana que pueda modelarse con cada expresión.
a. A – 500
b. 3B + 1
c. C • C
10. Resuelve los problemas .
a. Lee las afirmaciones.
Cualquier número par
se puede representar
como 2n, en que n es
un número natural.
Javiera Alberto
Cualquier número impar
se puede representar como
2n + 1, en que n es un
número natural.
• ¿Cuál de los niños hace una afirmación correcta?, ¿cómo lo sabes?
Respuesta:
• ¿Cuál de los niños hace una afirmación incorrecta?, ¿cómo lo sabes? [Profundización]
Respuesta:
b. Analiza la información.
El gobierno, a través del Ministerio de Transportes y Telecomunicaciones, se
propuso como meta que a 2022 haya 100 veces más vehículos eléctricos
en el parque automotor que en 2018.
Fuente: www.latercera.com. «La revolución de los autos eléctricos en Chile y el mundo». Noviembre, 2019.
• ¿Con qué expresión algebraica puedes representar la situación?
Respuesta:
Unidad 2 • La tecnología
68
CL0000000001374 MATE_6B_CA_U2_7150.indd 68 11-12-20 16:07](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-70-320.jpg)
![• Se estima que en 2018 había 120 autos eléctricos. ¿Cuántos habría en 2022?
Respuesta:
c. Analiza la oferta.
Precio original: C Descuento: $15 000 Precio final: $84 000
• ¿Qué ecuación permite modelarla?
Respuesta:
• ¿Cuál es el valor de C?
Respuesta:
d. El ancho de una cancha de fútbol debe medir entre 45 m y 90 m, y su largo, entre 90 m y
120 m. Considera una cancha en que el largo mide 35 metros más que el ancho.
• ¿Qué ecuación permite modelar su perímetro?, ¿y su área? [Profundización]
Respuesta:
• ¿Qué medidas puede tener la cancha? [Profundización]
Respuesta:
Crea un juego que requiera aplicar los aprendizajes que lograste en la lección. ¿Cuáles de los
contenidos te parecieron atractivos?, ¿cuáles no? Explica por qué.
Contenidos atractivos
Explicación:
Contenidos no atractivos
Explicación:
Sintetiza
Lección 5 • Patrones y lenguaje algebraico 69
CL0000000001374 MATE_6B_CA_U2_7150.indd 69 11-12-20 16:07](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-71-320.jpg)



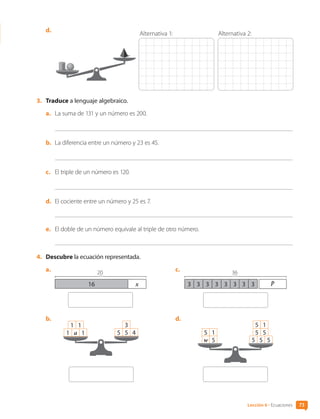

![6. Resuelve los problemas .
a. Observa la balanza equilibrada.
• ¿Qué ecuación se representa?
Respuesta:
• Juan dice que para resolver la ecuación se pueden retirar
de cada lado una de las incógnitas y 4 unidades. ¿Estás de
acuerdo con él o no?, ¿por qué?
Respuesta:
• ¿Cuál es el valor de la incógnita? Resuelve la ecuación planteada.
Respuesta:
• ¿Cómo puedes verificar en la balanza si el resultado es correcto?
Respuesta:
b. Ciencias Analiza la información. Verifica tus resultados en https://bit.ly/3asORjU.
Una estrategia para expresar en grados Fahrenheit (°F) una temperatura medida
en grados Celsius (°C) es multiplicar la cantidad de grados Celsius por 18, sumar
320 a este producto y el resultado dividirlo por 10.
• ¿Qué ecuación permite efectuar la transformación? Representa con C y F las incógnitas.
[Profundización]
Respuesta:
• ¿A cuántos grados Fahrenheit equivalen 10 °C?
Respuesta:
• ¿A cuántos grados Fahrenheit equivalen 25 °C?
Respuesta:
w 2 w
2
1 w 1
2 4 12
75
Lección 6 • Ecuaciones
CL0000000001374 MATE_6B_CA_U2_7150.indd 75 11-12-20 16:08](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-77-320.jpg)

![Etapa 3 (individual): Resuelve ahora la ecuación de la balanza que dibujaste.
Valor de la incógnita =
Etapa 4 (grupal): Comparen sus resultados y respondan.
• ¿Es correcta la afirmación de Lorena?, ¿por qué?
Respuesta:
• ¿Cuál sería la solución si se cuadruplica la cantidad de elementos en la balanza?, ¿y si se
aumenta en 9 veces?
Respuesta:
• ¿Qué conclusión pueden sacar de los resultados obtenidos?
Respuesta:
f. En un colegio se hizo una campaña para reunir la basura electrónica. [Profundización]
Curso A B Total
Basura electrónica (kg) 2x + 7 3x + 3 50
• ¿Cuántos kilogramos de basura electrónica se reunieron?
Respuesta:
• ¿Cuántos kilogramos recolectó el curso A?
Respuesta:
• ¿Cuántos kilogramos de diferencia hay entre lo recolectado por los cursos?
Respuesta:
• Para el próximo año, la meta es duplicar la cantidad de basura electrónica recolectada entre
ambos cursos. ¿Cuál es la ecuación que modela dicha meta?
Respuesta:
77
Lección 6 • Ecuaciones
CL0000000001374 MATE_6B_CA_U2_7150.indd 77 11-12-20 16:08](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-79-320.jpg)








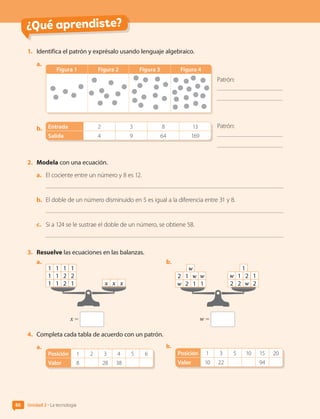
![5. Resuelve las ecuaciones.
a. 3n – 13 = 14
n =
b. h + 5 = 8 • 10
h =
c. 6q + 1 = 49
q =
d. 111 – 5k = 96
k =
6. Resuelve los problemas .
a. Observa las mascotas.
R kilogramos U kilogramos S kilogramos
¿Qué representa la expresión 2S + R =
U
2
?
Respuesta:
b. Lucas tiene (v + 8) videojuegos. Fabián tiene el doble de esta cantidad. Lucas tiene
11 videojuegos menos que Fabián. ¿Cuántos videojuegos tiene cada uno? [Profundización]
Respuesta:
Unidad 2
Para finalizar
¿Aprendiste estrategias nuevas
para resolver ecuaciones?
Sí Explica una de ellas.
No Crea una estrategia personal para hacerlo.
87
¿Qué aprendiste? • Evaluación de Unidad 2
CL0000000001374 MATE_6B_CA_U2_7150.indd 87 11-12-20 16:08](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-89-320.jpg)







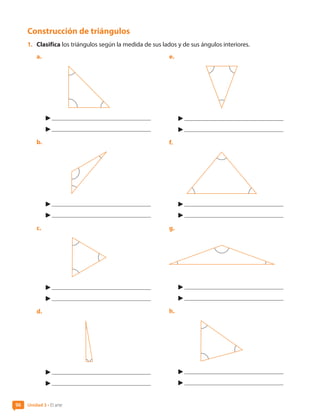
![2. Analiza las medidas de cada trío de segmentos e indica si es posible construir un triángulo
con ellos. Justifica.
a. 4 cm, 4 cm y 5 cm
b. 10 cm, 4 cm y 6 cm
c. 9 cm, 15 cm y 8 cm
d. 20 cm, 10 cm y 5 cm
e. 1 cm, 1 cm y 3 cm
f. 6 cm, 2 cm y 7 cm
3. Resuelve los problemas.
a. Dos de los ángulos interiores de un triángulo miden 30°. ¿Cuántos triángulos que cumplen
esta condición puedes dibujar?, ¿por qué? [Profundización]
Respuesta:
b. Dos lados de un triángulo isósceles miden 6 cm y 9 cm, respectivamente. ¿Cuántos triángulos
que cumplen esta condición puedes dibujar?, ¿por qué? [Profundización]
Respuesta:
Lección 7 • Construcciones geométricas 97
CL0000000001374 MATE_6B_CA_U3A_7804.indd 97 11-12-20 16:08](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-99-320.jpg)



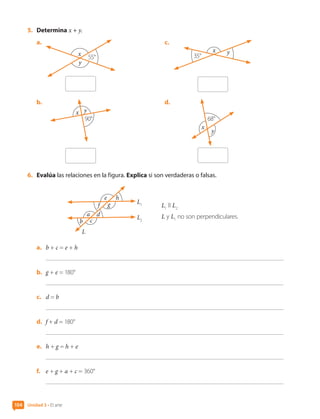
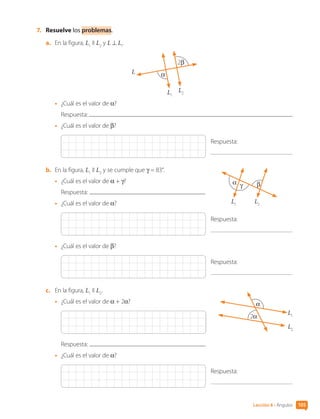




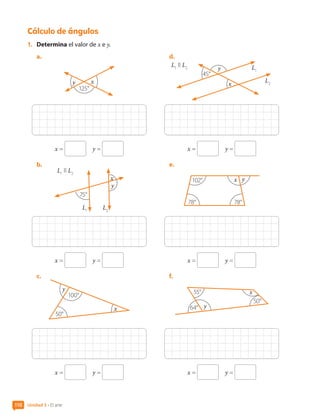
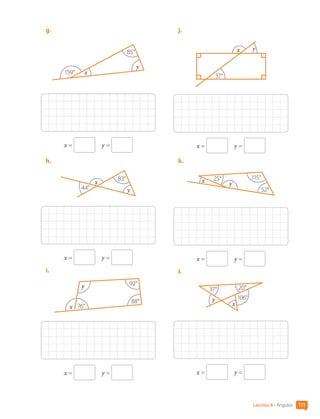
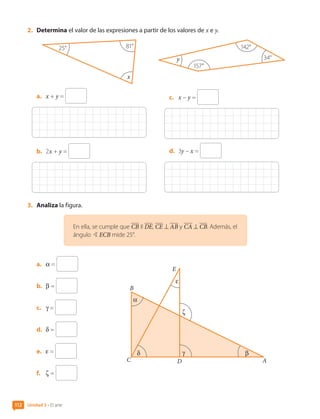





![6. Construye una teselación con la figura 2D.
a. Cuadrado.
b. Triángulo equilátero.
c. Hexágono regular.
7. Evalúa y escribe V (verdadero) o F (falso). Justifica.
a. Las figuras regulares tienen sus lados y ángulos interiores iguales.
b. Una teselación regular puede estar formada por rectángulos.
c. Es posible construir una teselación regular con triángulos equiláteros aplicando
únicamente traslaciones. [Profundización].
d. Es posible construir una teselación regular con cuadrados aplicando únicamente
traslaciones. [Profundización]
Unidad 3 • El arte
118
CL0000000001374 MATE_6B_CA_U3B_7760.indd 118 11-12-20 16:10](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-120-320.jpg)
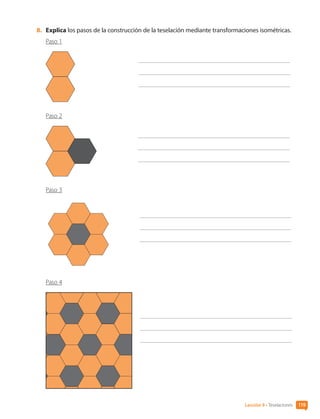




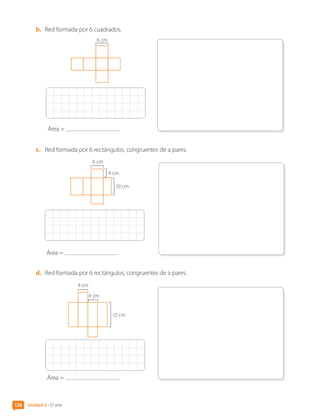

![Unidad 3 • El arte
128
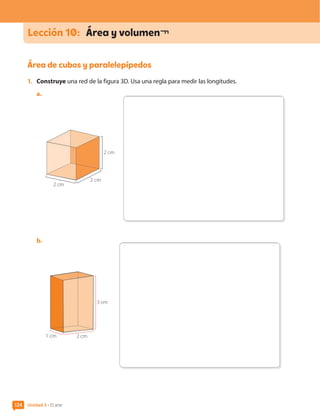
Cálculo del área de cubos y paralelepípedos
1. Determina el área A de un cubo cuya arista mide p y completa la tabla.
p (cm) A (cm2
)
1
3
5
7
9
11
20
24
2. Determina el área A de los paralelepípedos y completa la tabla.
Alto (cm) Largo (cm) Ancho (cm) A (cm2
)
1 5 2
3 6 4
6 8 6
4 6 5
3 10 2
7 11 7
9 10 8
5 11 10
2 5 3,5
1,5 8 3
4 5,5 4
3 9,5 7
3. Determina la longitud p de la arista de un cubo de área A y completa la tabla. [Profundización]
A (cm2
) p (cm)
24
96
216
384
600
726
1 944
CL0000000001374 MATE_6B_CA_U3B_7760.indd 128 11-12-20 16:10](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-130-320.jpg)
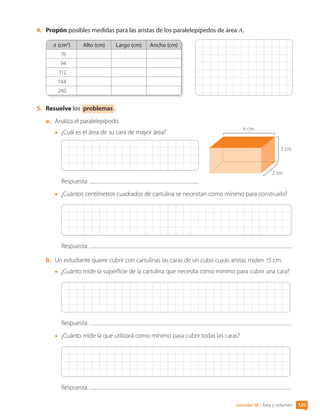
![Unidad 3 • El arte
130
c. Alejandro y Natalia construyeron paralelepípedos con el mínimo posible de cartón. El de
Alejandro mide 20 cm de alto, 15 cm de largo y 10 cm de ancho. El de Natalia, 18 cm de alto,
15 cm de largo y 12 cm de ancho.
• ¿Cuánto cartón ocupó Alejandro?
Respuesta:
• ¿Cuánto cartón utilizó Natalia?
Respuesta:
• ¿Cuál de los niños empleó más cartón en su construcción?
Respuesta:
d. La figura se armó con 5 cubos cuyas aristas miden 7,5 cm. [Profundización]
• ¿Cuál es el área de uno de los cubos?
Respuesta:
• ¿Cuál es el área de la figura compuesta?
Respuesta:
CL0000000001374 MATE_6B_CA_U3B_7760.indd 130 17-12-20 10:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-132-320.jpg)
![Lección 10 • Área y volumen 131
e. La figura se armó con cubos cuyas aristas miden 5 cm. [Profundización]
• ¿Cuál es el área de uno de los cubos?
Respuesta:
• ¿Cuál es el área de la figura compuesta?
Respuesta:
f. Adriana va a pintar las paredes y el cielo de su pieza. Esta tiene forma de paralelepípedo,
cuyo alto, largo y ancho son 2,5 m, 4 m y 3,5 m, respectivamente. Además, hay 2 ventanas
cuadradas de 1 m de lado. [Profundización]
• ¿Cuál es el área de las paredes de su pieza?
Respuesta:
• ¿Cuál es el área del cielo de su pieza?
Respuesta:
• ¿Cuál es el área total que pintará Adriana?
Respuesta:
CL0000000001374 MATE_6B_CA_U3B_7760.indd 131 11-12-20 16:10](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-133-320.jpg)
![Unidad 3 • El arte
132
Cálculo del volumen de cubos y paralelepípedos
1. Determina el volumen V de un cubo cuya arista mide q y completa la tabla.
q (cm) V (cm3
)
1
2
3
4
5
6
7
8
9
10
11
12
2. Determina el área V de los paralelepípedos y completa la tabla.
Alto (cm) Largo (cm) Ancho (cm) V (cm3
)
4 9 8
5 10 7
9 13 9
1 25 2
4 20 12
12 22 15
10 32 10
19 29 15
2,5 8 5
3 11 3,5
9 10,5 7
8 8,5 8
3. Determina la longitud q de la arista de un cubo de volumen V y completa la tabla. [Profundización]
V (cm3
) q (cm)
27
64
125
343
1 000
CL0000000001374 MATE_6B_CA_U3B_7760.indd 132 11-12-20 16:10](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-134-320.jpg)
![4. Resuelve los problemas .
a. La figura se armó con cubos cuyas aristas miden 3,5 cm. [Profundización]
• ¿Cuál es el volumen de uno de los cubos?
Respuesta:
• ¿Cuál es el volumen de la figura compuesta?
Respuesta:
Respuesta:
b. Las aristas basales de un paralelepípedo miden 3 cm y 2 cm; y su altura, 6 cm. [Profundización]
• Si su altura aumenta al doble, ¿en qué porcentaje se incrementa su volumen?
Respuesta:
Respuesta:
• Si cada arista aumenta al doble, ¿cuál es la razón entre sus volumenes final e inicial?
Respuesta:
Respuesta:
Crea una maqueta de cartón a partir de la red de un cubo o paralelepípedo, y calcula su área
y su volumen. ¿Qué contenidos de los estudiados has aplicado en otras asignaturas?, ¿cuáles
no? Describe un ejemplo en cada caso.
Contenidos aplicados
Ejemplo:
Contenidos no aplicados
Ejemplo:
Sintetiza
Lección 10 • Área y volumen 133
CL0000000001374 MATE_6B_CA_U3B_7760.indd 133 17-12-20 10:13](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-135-320.jpg)



![5. Dibuja y recorta triángulos equiláteros congruentes.
a. Construye una teselación con ellos y represéntala.
b. ¿Qué transformaciones isométricas aplicaste para construir la teselación?
Respuesta:
c. ¿Cómo clasificas la teselación?
Respuesta:
6. En la figura se cumple que L1
L2
.
a. ¿Cuáles son los valores de α y β?
Respuesta:
b. ¿Qué relación existe entre α y β?
Respuesta:
7. Resuelve el problema . [Profundización]
La figura está formada por cubos cuya arista mide 6 cm.
¿Cuál es la razón entre su área y su volumen?
Respuesta:
115°
L1
L2
α
β
Unidad 3
Para finalizar
¿Te ayuda lo aprendido en
esta unidad a comprender
mejor tu entorno?
Sí Da un ejemplo.
No Enumera figuras 2D que observas a tu alrededor.
137
¿Qué aprendiste? • Evaluación de Unidad 3
CL0000000001374 MATE_6B_CA_U3B_7760.indd 137 11-12-20 16:10](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-139-320.jpg)




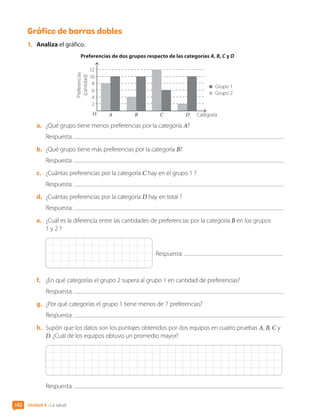
![2. Resuelve los problemas.
a. Dos amigos compiten en un juego que se divide en cuatro etapas. El puntaje que obtuvieron
se representa a continuación:
Puntaje en cuatro etapas de un juego
Etapa (n°)
2
O
4
6
8
10
12
14
16
18
Puntaje
(puntos)
Diego
Mónica
1 2 3 4
• ¿Cuántos puntos obtuvo Diego en la etapa 3?
Respuesta:
• ¿Cuántos puntos logró Mónica en la etapa 1?
Respuesta:
• ¿En qué etapa Mónica tuvo su puntaje menor?
Respuesta:
• ¿Cuál fue la diferencia de puntajes en la etapa 2?
Respuesta:
• ¿Cuál de los niños tenía un puntaje acumulado mayor al cabo de la segunda etapa?
Respuesta:
• Gana el juego el que obtiene más puntaje acumulado en las cuatro etapas. ¿Cuál de los
niños ganó el juego? [Profundización]
Respuesta:
Lección 11 • Representación de datos 143
CL0000000001374 MATE_6B_CA_U4A_7752.indd 143 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-145-320.jpg)
![b. El gráfico representa las ventas semanales en dos tiendas de juegos.
Ventas semanales de dos tiendas de juegos
Tipo de juego
5
O
10
15
20
25
30
35
40
Venta
(cantidad)
Tienda 1
Tienda 2
Consolas Juegos de mesa Bicicletas
• ¿Qué tienda vendió más juegos de mesa?
Respuesta:
• ¿Cuántas bicicletas vendió la tienda 2?
Respuesta:
• ¿Cuántas consolas vendieron las dos tiendas en conjunto?
Respuesta:
• ¿Cuál de los tres juegos se vendió más en la tienda 2?
Respuesta:
• ¿Cuál de las tiendas vendió más bicicletas?
Respuesta:
• ¿Cuál de las tiendas vendió una mayor cantidad de juegos?
Respuesta:
• El precio de una consola es de $18 000 en la tienda 1 y de $24 500 en la tienda 2. ¿Cuál de
las tiendas recibió más dinero por la venta de consolas? [Profundización]
Respuesta:
Unidad 4 • La salud
144
CL0000000001374 MATE_6B_CA_U4A_7752.indd 144 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-146-320.jpg)
![c. El gráfico se construyó a partir de encuestas realizadas a nivel nacional. En él se muestra la
evolución de dos de las respuestas a una de las preguntas planteadas.
Fuente: Ministerio del Deporte. «Encuesta Nacional de Actividad
Física y Deporte en Población de 18 años y más, 2018».
Habitualmente, ¿qué hace usted en su tiempo libre?
Tiempo (año)
O
Porcentaje
(%) Veo televisión.
Practico un deporte
o actividad física.
5
15
25
10
20
2006 2009 2012 2015 2018
• ¿Cuál de las dos respuestas fue más frecuente en todos los años considerados?
Respuesta:
• ¿Qué porcentaje de los encuestados, aproximadamente, preferían ver televisión en 2012?
Respuesta:
• ¿Qué porcentaje de los encuestados, aproximadamente, preferían practicar un deporte o
actividad física en 2006?
Respuesta:
• ¿En qué año la diferencia porcentual entre las dos respuestas fue menor?
Respuesta:
• ¿Qué tendencia a lo largo del tiempo se produce en el porcentaje de encuestados que
declaran practicar un deporte o actividad física?
Respuesta:
• Supón que se encuestó a 6 000 personas en 2012. ¿Cuántos de ellos declararon practicar un
deporte o actividad física? [Profundización]
Respuesta:
Lección 11 • Representación de datos 145
CL0000000001374 MATE_6B_CA_U4A_7752.indd 145 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-147-320.jpg)

![3. Un robot realizó cuatro tipos de movimientos: arriba, abajo, izquierda y derecha. El
porcentaje de cada tipo de movimiento realizado se muestra en el gráfico circular de la
imagen. Completa la tabla con la cantidad de movimientos de cada tipo que realizó.
24 %
Derecha
Abajo
Izquierda
Arriba
20 % Tipo de movimiento Movimientos (cantidad)
Arriba
Abajo
Izquierda
Derecha
4. Construye un gráfico circular a partir de la tabla de datos. [Profundización]
Tipo de fruta Porcentaje (%)
Manzana 25
Pera 25
Naranja 50
5. Resuelve los problemas.
a. Analiza el gráfico con los resultados de un equipo de fútbol en un torneo.
• ¿Cuánto suman los porcentajes del gráfico?
Respuesta:
• ¿Cuál es la razón entre los partidos ganados
y perdidos?
Respuesta:
• El equipo jugó 20 partidos en el torneo. ¿Cuántos ganó, empató y perdió?
Respuesta:
Porcentaje de partidos ganados,
empatados y perdidos
25 %
60 %
15 %
Ganados
Empatados
Perdidos
12 %
44 %
Lección 11 • Representación de datos 147
CL0000000001374 MATE_6B_CA_U4A_7752.indd 147 17-12-20 10:27](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-149-320.jpg)
![b. Analiza el gráfico que representa el destino de 300 pasajeros de un avión que despegó de Iquique.
Destino de pasajeros del vuelo
25 %
10 %
50 %
Antofagasta
Santiago
Concepción
Punta Arenas
• ¿Qué porcentaje de los pasajeros descenderá en su primera parada, Antofagasta?
Respuesta:
• ¿A cuántos pasajeros equivale ese porcentaje?
Respuesta:
• ¿Cuántos de los pasajeros que se embarcaron en Iquique descenderán en Punta Arenas?
Respuesta:
6. Dos integrantes.
Etapa 1 (grupal): Analicen la tabla. Calculen los porcentajes y los ángulos asociados a cada
categoría. Como a un círculo se le puede asociar una medida de 360°, pueden expresar cada
porcentaje como una razón de consecuente 360. Anoten sus resultados en la tabla. [Profundización]
Categoría
Preferencias
(cantidad)
Porcentaje
(%)
Medida del
ángulo (°)
A 60
B 50
C 25
D 65
Total
Unidad 4 • La salud
148
CL0000000001374 MATE_6B_CA_U4A_7752.indd 148 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-150-320.jpg)


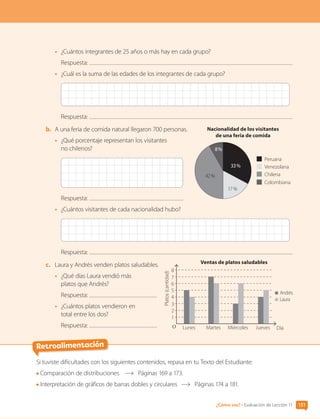

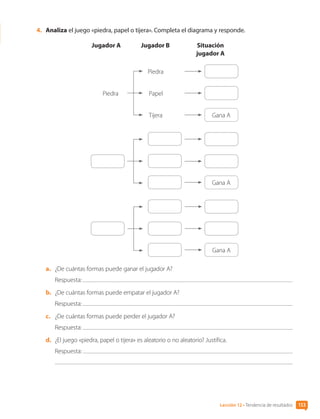

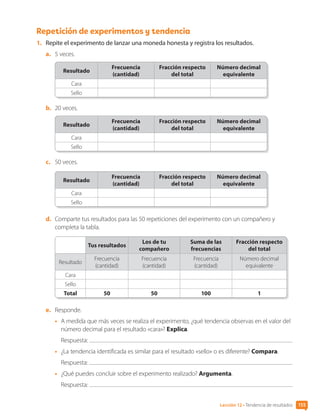
![2. Se lanza una moneda muchas veces. Los resultados se registran en la tabla.
Resultado Cara Sello
Frecuencia (cantidad) 748 752
a. ¿Cuántas veces se lanzó la moneda?
Respuesta:
b. Determina la fracción respecto del total de cada resultado del experimento. Propón una
conjetura para asociar esta fracción con la posibilidad de que se verifique el resultado.
[Profundización]
Respuesta:
c. Simula el experimento en una hoja de cálculo. Compara tus resultados con los de la tabla de
esta actividad. ¿Son iguales o distintos?, ¿por qué?
Respuesta:
3. En una tómbola hay bolitas con los números 1 al 5. Se extrae una bolita, se registra su
número y se devuelve a la tómbola. Analiza la tabla y complétala.
Número
obtenido
Frecuencia
(cantidad)
Fracción respecto del total
1 6
2 5
3 6
4 12
5 6
a. ¿Cuántas veces se repitió el experimento?
Respuesta:
b. ¿Qué fracción obtuviste en la tercera columna para cada número obtenido?
Respuesta:
c. ¿Qué número tiene más posibilidades de obtenerse en la tómbola? Haz una conjetura.
Justifica. [Profundización]
Respuesta:
Unidad 4 • La salud
156
CL0000000001374 MATE_6B_CA_U4B_7757.indd 156 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-158-320.jpg)

![Sintetiza
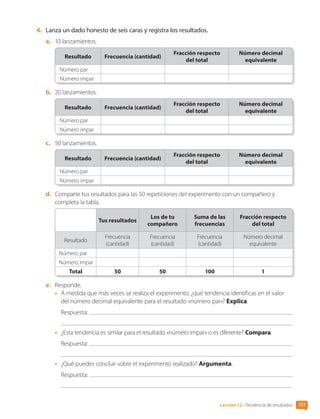
6. Resuelve el problema.
En una urna hay bolitas con los números 1, 2, 3, 4 y 5 pintados en su superficie. Se extrae
una bolita, se anota el resultado y se devuelve a la urna. Los resultados de repetir este
experimento 5 000 veces se muestran en la tabla.
Resultado (n°) 1 2 3 4 5
Frecuencia (cantidad) 1 201 789 703 1 309 998
a. El experimento realizado, ¿es aleatorio o no aleatorio?
Respuesta:
b. ¿Cuál es la razón parte-todo asociada a cada resultado?
1 2 3 4 5
c. ¿Qué número tiene mayor posibilidad de ser seleccionado? Realiza una conjetura.
Respuesta:
d. Supón que la urna tiene 100 bolitas. ¿Cuántas tendrían pintado en su superficie cada número:
1, 2, 3, 4 y 5? Realiza conjeturas y calcula. [Profundización]
1 2 3 4 5
Simula un experimento aleatorio usando una hoja de cálculo y plantea diversas conjeturas.
¿Cuáles de los contenidos estudiados en la lección te resultaron entretenidos?, ¿cuáles no?
Explica por qué.
Contenidos entretenidos
Explicación:
Contenidos no entretenidos
Explicación:
Lección 12 • Tendencia de resultados 159
CL0000000001374 MATE_6B_CA_U4B_7757.indd 159 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-161-320.jpg)



![b. Los resultados de una prueba de cuatro preguntas se muestran a continuación:
Resultados de una prueba de cuatro preguntas
Correcta
Incorrecta
O
5
15
20
10
25
1 2 3 4 Pregunta (n°)
• ¿Qué pregunta presenta una mayor diferencia entre correctas e incorrectas?
Respuesta:
• ¿En qué preguntas hubo más respuestas correctas que incorrectas?
Respuesta:
• ¿Cuántos estudiantes rindieron la prueba?
Respuesta:
c. Se lanza 500 veces un dado de seis caras. [Profundización]
Resultado (n°) 1 2 3 4 5 6
Frecuencia (cantidad) 83 86 87 78 85 81
• ¿Qué fracción conjeturas que expresa la probabilidad de obtener un número múltiplo de 3?
Respuesta:
• ¿Qué fracción conjeturas que expresa la probabilidad de obtener un número par?
Respuesta:
• ¿Te ayudaron los contenidos
de esta unidad a comprender
información de tu entorno?
Sí Da un ejemplo.
No
Nombra dos situaciones en las que has oído
hablar de información estadística o de azar.
Unidad 4
para finalizar
Estudiantes
(cantidad)
163
¿Qué aprendiste? • Evaluación de Unidad 4
CL0000000001374 MATE_6B_CA_U4B_7757.indd 163 11-12-20 16:11](https://image.slidesharecdn.com/cuadernodeactividades6to-210421065313/85/Cuaderno-de-actividades-6to-165-320.jpg)