Este documento presenta el texto para el curso de matemáticas de 6o básico. Incluye capítulos sobre números, álgebra, geometría, probabilidad y estadística. Cada capítulo contiene lecciones, ejercicios de práctica y evaluaciones. El texto fue diseñado por expertos estadounidenses y adaptado al currículo chileno por la editorial Galileo.












































































































































































































































































































![296
3. Ver cuaderno del estudiante
4. Ver cuaderno del estudiante
5. Ver cuaderno del estudiante
6. Ver cuaderno del estudiante
7. Ver cuaderno del estudiante
8. Ver cuaderno del estudiante
Página 206
1. Triángulo escaleno
2. Triángulo equilátero
3. Acutángulo
4. Triángulo rectángulo y escaleno
5. Triángulo rectángulo y escaleno
6. Triángulo acutángulo y equilátero
7. Triángulo obtusángulo e isósceles
8. No siempre
9. No siempre
10. Nunca
11. Siempre
12. Ver cuaderno del estudiante
13. Ver cuaderno del estudiante
14. Ver cuaderno del estudiante
15. 31°
16. 45°
17. 110°
18. Un hexágono
19. 16 cajas
20. 6 ; respuesta abierta
Página 207
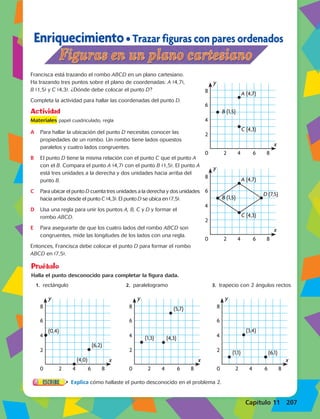
1. ( 2 , 6 )
2. ( 2 , 7 )
3. ( 6 , 4 )
Págs. 208 y 209
1. A
2. B
3. D
4. C
5. Respuesta abierta
6. A
7. A
8. A
9. B
10. A
11. Respuesta abierta
12. D
13. B
14. C
15. A
16. A
Capítulo 12
Página 211
1. Sí
2. No
3. No
4. Sí
5. Sí
6. No
7. No
8. Sí
9. 3/4
10. 8/8
11. 1/4
12. 1/2
Capítulo 12 · Lección 1
Página 212
1. Respuesta abierta
2. Respuesta abierta
3. Respuesta abierta
4. Respuesta abierta
5. Respuesta abierta
6. Respuesta abierta
Página 213
7. a) traslación
b) simetrías o rotaciones
c) traslación
d) traslación
e) rotación
f) traslación
Página 214
8. Regular
9. Semi regular
10. No regular
Página 215
11. Pentágono
12. Trapecios, triángulos y hexágonos
13. hexágono
14. octágonos
15. Traslación, rotación, reflexión
16. Semi regular; triángulos y
pentágonos
17. Semi regular; triángulos y
hexágonos
18. Respuesta abierta
19. Reflexión; respuesta abierta,
traslación
20. Sí; respuesta abierta
21. Un cuadrado
22. Si se puede
23. Ver cuaderno del estudiante
24. Respuesta abierta
25. No regular; Semi regular y regular
26. 360°
Capítulo 12 · Lección 2
Página 217
1. Ver cuaderno del estudiante
2. Aumentar 2; ver cuaderno del
estudiante
3. Círculo grande y puntito al norte,
Círculo chico y puntito al norte;
círculo grande y puntito al este,
círculo chico y puntito al este y así
sucesivamente. Ver cuaderno del
estudiante
4. Un triángulo grande y tres
pequeños. Ver cuaderno del
estudiante
5. Respuesta abierta
6. Se añade un cuadrado y un
círculo a la figura. Ver cuaderno del
estudiante
7. Caritas rotan en sentido contrario
de las manecillas del reloj hasta
llegar a la posición original y así
sucesivamente. Ver cuaderno del
estudiante
8. Primer cuadrado con esquina
oscura en la parte inferior derecha
y segundo cuadrado con la esquina
oscura en la parte inferior izquier-da.
Ver cuaderno del estudiante
9. Ver cuaderno del estudiante
10. Ver cuaderno del estudiante
11. Ver cuaderno del estudiante
12. Sí; respuesta abierta
13. Son cuadrados y en su interior se
alternan rombos y cuadrados de
distintos colores. Comenzaría con
un cuadrado y en su interior un
rombo y así sucesivamente.
14. Traslación a la derecha o izquierda
y rotación en 180°
15. Respuesta abierta
16. Sí
17. Rectángulo
18. Triángulo
19. A
Página 218
Grupo A
1. Sí es posible. Ver cuaderno del
estudiante
2. Ver cuaderno el estudiante
Grupo B
1. Hexágono= 720° y 9 diagonales;
Octógono= 1 080° y 20 diagonales.
Respuesta abierta
2. 2 u2 ; 6 u2 ; 12 u2 ; 20 u2 y 30 u2
Página 220
1. Congruentes
2. Teselación
3. No regular
4. No regular
5. Semi regular
6. Cuadrados; triángulos y hexágonos
7. Rectángulos; triángulos y
hexágonos
8. Cuadrados; triángulos; rectángulos
y paralelogramos
9. Se aumenta el doble de la
figura anterior. Ver cuaderno del
estudiante
10. Respuesta abierta
Página 221
1. Ver cuaderno del estudiante
2. Ver cuaderno del estudiante
3. Ver cuaderno del estudiante
4. Ver cuaderno del estudiante
5. Respuesta abierta
6. Respuesta abierta
Páginas 222 y 223
1. C
2. C
3. A
4. No, respuesta abierta
5. C
6. D
7. B
8. (1,6 · 2) · d
9. C
10. Respuesta abierta
11. A
12. C
13. D
14. Respuesta abierta
Capítulo 13
Página 225
1. recto
2. agudo
3. obtuso
4. agudo
5. Rectángulo
6. Triángulo
7. Triángulo
8. Cuadrado
9. Triángulo
10. Pentágono
Capítulo 13 · Lección 1
Página 228
1. 11 • 21=462 ; 5 • 21=210 ;
11 • 5=110.
Área total = 782 cm2
2. 24 m2
3. 4,5 cm2
4. 8 16/25 cm2
5. 164 cm2
6. Respuesta abierta
7. 158 m2
8. 150 cm2
9. 363,3 cm2
10. 115 3/4 m2
11. 1 350 m2
12. 73,5
13. 121 1/2
14. 15 000
15. 352 cm2
16. 21 400
17. Ver cuaderno
18. Ver cuaderno
Página 229
19. 782 cm2
20. 483 300 m2
21. Respuesta abierta
22. Paralelogramos
23. 63 m2
24. D
25. 884 m2
Poder Matemático
1. 382 cm2
Capítulo 13 · Lección 2
Página 232
1. 3 750 cm3
2. 270 m3
3. 128 cm3
4. Respuesta abierta
5. 1,024 cm3
6. 33 600 m3
7. 166 3/8 cm3
8. 12 cm
9. 12,7 cm
10. 5 cm
11. 37,5 m3
12. 2 cm
Página 233
13. Ver cuaderno del estudiante
14. A= 13 1/2 m2 y V= 3 3/8 m3 ;
respuesta abierta
15. 52 cm2.
16. Respuesta abierta
17. 17 es igual a un número aumen-tado
en 9
18. A
19. 3,85 ; 3,58 ; 3,508 ; 3,08
20. B
Poder Matemático
1. Se reduciría el volumen, sería
36 cm3
2. Aumentaría el volumen, sería 1
152 cm3
3. No cambiaría, seguiría siendo el
volumen 288 cm3
4. Respuesta abierta
Capítulo 13 · Lección 3
Página 236
1. Hay 315 cm3 de diferencia
2. Aumentaría el volumen
3. 144 cm3
4. 1 500 cm3
5. La diferencia es de 750 cm3
6. Sacarle centímetros a cada lazo
7. 17 caras
8. 100 cm3, respuesta abierta
Página 237
9. La cuarta caja es 4 veces más
grande que la segunda
10. No, respuesta abierta
11. Respuesta abierta
12. $ 1 831 aprox.
13. Sí
14. Roberto, Martina, Valentina y
Nicolás
15. Respuesta abierta
16. Sí
17. $ 2 500
Página 238
Grupo A
1. 526 cm2
2. A= 113 cm2
3. 384 m2
4. A= 86,64 m2
5. A= 3 300 cm2
6. 20 m
Grupo B
1. V= 1 386 mm3
2. V= 216 m3
3. V= 74,214 cm3
4. Con A
5. Con B
8. 6 750 cm3
9. 750 cm3
Página 240
1. Área total
2. Volumen
3. A= 907,74 cm2
4. A= 3 060 m2
5. A= 94 1/2 cm2
6. V= 62 712 mm3
7. V= 3 997,76 m3
8. V= 753,571 m3
9. 19 cm
10. 70 cm
11. 5 cm
12. 12,375 m3
13. Respuesta abierta
Página 241
1. Fig.1, V= 90 cm3; fig.2, V= 720
cm3. Tiene 8 veces más volumen
la fig.2
2. Fig.1, V= 343 cm3; fig.2, V= 2
744 cm3, fig.3, V= 9 261. Va
aumentando
3. Sí, si el lado aumenta n veces, el
volumen crece n3 veces.
Págs. 242 y 243
1. D
2. C
3. C
4. D
5. B
6. A
7. D
8. C
9. A
10. D
11. A
12. A
13. C
14. D
15. 7,4 km
16. 43,5 cm
17. V
18. F
19. V
20. Respuesta abierta
21. Área rectángulo 1= 105 cm2 y área
de triángulo 1= 612,5 cm2
Capítulo 14
Página 249
1. $ 400
2. No
3. Julio y septiembre
4. $ 800
5. Fútbol
6. Natación
7. 4 personas
8. 4 personas
Capítulo 14 · Lección 1
Página 250
1. Sí, respuesta abierta
Página 251
2. Ver cuaderno del estudiante
3. En películas
4. Espectáculo en vivo
5. Respuesta abierta
6. Ver cuaderno del estudiante
7. Subsidios de gobierno
8. Contribuciones privadas
9. Suspenso y Ciencia ficción
10. 136 personas por romance, 64 por
comedia, 84 por acción, 52 por
ciencia ficción y 36 por suspenso
11. Respuesta abierta
12. Suspenso
13. Con información de dos conjuntos
de datos y compararlos
14. Contribuciones privadas
15. Comedia
Capítulo 14 · Lección 2
Página 253
1. Ver cuaderno del estudiante
2. 8 días
3. 25
4. 1, porque hay una x en los 30°
5. 30°. Respuesta abierta
6. 16
7. [7 – 15]
8. Sí, 15
9. Ver cuaderno del estudiante
10. Diagrama de tallo y hojas
11. 9 años
12. 15
13. 33
14. Aquella que puede usarse para
mostrar cuántas veces aparece
cada valor de datos](https://image.slidesharecdn.com/libromat6-141102190941-conversion-gate02/85/Libro-mat-6-307-320.jpg)














![296
3. Ver cuaderno del estudiante
4. Ver cuaderno del estudiante
5. Ver cuaderno del estudiante
6. Ver cuaderno del estudiante
7. Ver cuaderno del estudiante
8. Ver cuaderno del estudiante
Página 206
1. Triángulo escaleno
2. Triángulo equilátero
3. Acutángulo
4. Triángulo rectángulo y escaleno
5. Triángulo rectángulo y escaleno
6. Triángulo acutángulo y equilátero
7. Triángulo obtusángulo e isósceles
8. No siempre
9. No siempre
10. Nunca
11. Siempre
12. Ver cuaderno del estudiante
13. Ver cuaderno del estudiante
14. Ver cuaderno del estudiante
15. 31°
16. 45°
17. 110°
18. Un hexágono
19. 16 cajas
20. 6 ; respuesta abierta
Página 207
1. ( 2 , 6 )
2. ( 2 , 7 )
3. ( 6 , 4 )
Págs. 208 y 209
1. A
2. B
3. D
4. C
5. Respuesta abierta
6. A
7. A
8. A
9. B
10. A
11. Respuesta abierta
12. D
13. B
14. C
15. A
16. A
Capítulo 12
Página 211
1. Sí
2. No
3. No
4. Sí
5. Sí
6. No
7. No
8. Sí
9. 3/4
10. 8/8
11. 1/4
12. 1/2
Capítulo 12 · Lección 1
Página 212
1. Respuesta abierta
2. Respuesta abierta
3. Respuesta abierta
4. Respuesta abierta
5. Respuesta abierta
6. Respuesta abierta
Página 213
7. a) traslación
b) simetrías o rotaciones
c) traslación
d) traslación
e) rotación
f) traslación
Página 214
8. Regular
9. Semi regular
10. No regular
Página 215
11. Pentágono
12. Trapecios, triángulos y hexágonos
13. hexágono
14. octágonos
15. Traslación, rotación, reflexión
16. Semi regular; triángulos y
pentágonos
17. Semi regular; triángulos y
hexágonos
18. Respuesta abierta
19. Reflexión; respuesta abierta,
traslación
20. Sí; respuesta abierta
21. Un cuadrado
22. Si se puede
23. Ver cuaderno del estudiante
24. Respuesta abierta
25. No regular; Semi regular y regular
26. 360°
Capítulo 12 · Lección 2
Página 217
1. Ver cuaderno del estudiante
2. Aumentar 2; ver cuaderno del
estudiante
3. Círculo grande y puntito al norte,
Círculo chico y puntito al norte;
círculo grande y puntito al este,
círculo chico y puntito al este y así
sucesivamente. Ver cuaderno del
estudiante
4. Un triángulo grande y tres
pequeños. Ver cuaderno del
estudiante
5. Respuesta abierta
6. Se añade un cuadrado y un
círculo a la figura. Ver cuaderno del
estudiante
7. Caritas rotan en sentido contrario
de las manecillas del reloj hasta
llegar a la posición original y así
sucesivamente. Ver cuaderno del
estudiante
8. Primer cuadrado con esquina
oscura en la parte inferior derecha
y segundo cuadrado con la esquina
oscura en la parte inferior izquier-da.
Ver cuaderno del estudiante
9. Ver cuaderno del estudiante
10. Ver cuaderno del estudiante
11. Ver cuaderno del estudiante
12. Sí; respuesta abierta
13. Son cuadrados y en su interior se
alternan rombos y cuadrados de
distintos colores. Comenzaría con
un cuadrado y en su interior un
rombo y así sucesivamente.
14. Traslación a la derecha o izquierda
y rotación en 180°
15. Respuesta abierta
16. Sí
17. Rectángulo
18. Triángulo
19. A
Página 218
Grupo A
1. Sí es posible. Ver cuaderno del
estudiante
2. Ver cuaderno el estudiante
Grupo B
1. Hexágono= 720° y 9 diagonales;
Octógono= 1 080° y 20 diagonales.
Respuesta abierta
2. 2 u2 ; 6 u2 ; 12 u2 ; 20 u2 y 30 u2
Página 220
1. Congruentes
2. Teselación
3. No regular
4. No regular
5. Semi regular
6. Cuadrados; triángulos y hexágonos
7. Rectángulos; triángulos y
hexágonos
8. Cuadrados; triángulos; rectángulos
y paralelogramos
9. Se aumenta el doble de la
figura anterior. Ver cuaderno del
estudiante
10. Respuesta abierta
Página 221
1. Ver cuaderno del estudiante
2. Ver cuaderno del estudiante
3. Ver cuaderno del estudiante
4. Ver cuaderno del estudiante
5. Respuesta abierta
6. Respuesta abierta
Páginas 222 y 223
1. C
2. C
3. A
4. No, respuesta abierta
5. C
6. D
7. B
8. (1,6 · 2) · d
9. C
10. Respuesta abierta
11. A
12. C
13. D
14. Respuesta abierta
Capítulo 13
Página 225
1. recto
2. agudo
3. obtuso
4. agudo
5. Rectángulo
6. Triángulo
7. Triángulo
8. Cuadrado
9. Triángulo
10. Pentágono
Capítulo 13 · Lección 1
Página 228
1. 11 • 21=462 ; 5 • 21=210 ;
11 • 5=110.
Área total = 782 cm2
2. 24 m2
3. 4,5 cm2
4. 8 16/25 cm2
5. 164 cm2
6. Respuesta abierta
7. 158 m2
8. 150 cm2
9. 363,3 cm2
10. 115 3/4 m2
11. 1 350 m2
12. 73,5
13. 121 1/2
14. 15 000
15. 352 cm2
16. 21 400
17. Ver cuaderno
18. Ver cuaderno
Página 229
19. 782 cm2
20. 483 300 m2
21. Respuesta abierta
22. Paralelogramos
23. 63 m2
24. D
25. 884 m2
Poder Matemático
1. 382 cm2
Capítulo 13 · Lección 2
Página 232
1. 3 750 cm3
2. 270 m3
3. 128 cm3
4. Respuesta abierta
5. 1,024 cm3
6. 33 600 m3
7. 166 3/8 cm3
8. 12 cm
9. 12,7 cm
10. 5 cm
11. 37,5 m3
12. 2 cm
Página 233
13. Ver cuaderno del estudiante
14. A= 13 1/2 m2 y V= 3 3/8 m3 ;
respuesta abierta
15. 52 cm2.
16. Respuesta abierta
17. 17 es igual a un número aumen-tado
en 9
18. A
19. 3,85 ; 3,58 ; 3,508 ; 3,08
20. B
Poder Matemático
1. Se reduciría el volumen, sería
36 cm3
2. Aumentaría el volumen, sería 1
152 cm3
3. No cambiaría, seguiría siendo el
volumen 288 cm3
4. Respuesta abierta
Capítulo 13 · Lección 3
Página 236
1. Hay 315 cm3 de diferencia
2. Aumentaría el volumen
3. 144 cm3
4. 1 500 cm3
5. La diferencia es de 750 cm3
6. Sacarle centímetros a cada lazo
7. 17 caras
8. 100 cm3, respuesta abierta
Página 237
9. La cuarta caja es 4 veces más
grande que la segunda
10. No, respuesta abierta
11. Respuesta abierta
12. $ 1 831 aprox.
13. Sí
14. Roberto, Martina, Valentina y
Nicolás
15. Respuesta abierta
16. Sí
17. $ 2 500
Página 238
Grupo A
1. 526 cm2
2. A= 113 cm2
3. 384 m2
4. A= 86,64 m2
5. A= 3 300 cm2
6. 20 m
Grupo B
1. V= 1 386 mm3
2. V= 216 m3
3. V= 74,214 cm3
4. Con A
5. Con B
8. 6 750 cm3
9. 750 cm3
Página 240
1. Área total
2. Volumen
3. A= 907,74 cm2
4. A= 3 060 m2
5. A= 94 1/2 cm2
6. V= 62 712 mm3
7. V= 3 997,76 m3
8. V= 753,571 m3
9. 19 cm
10. 70 cm
11. 5 cm
12. 12,375 m3
13. Respuesta abierta
Página 241
1. Fig.1, V= 90 cm3; fig.2, V= 720
cm3. Tiene 8 veces más volumen
la fig.2
2. Fig.1, V= 343 cm3; fig.2, V= 2
744 cm3, fig.3, V= 9 261. Va
aumentando
3. Sí, si el lado aumenta n veces, el
volumen crece n3 veces.
Págs. 242 y 243
1. D
2. C
3. C
4. D
5. B
6. A
7. D
8. C
9. A
10. D
11. A
12. A
13. C
14. D
15. 7,4 km
16. 43,5 cm
17. V
18. F
19. V
20. Respuesta abierta
21. Área rectángulo 1= 105 cm2 y área
de triángulo 1= 612,5 cm2
Capítulo 14
Página 249
1. $ 400
2. No
3. Julio y septiembre
4. $ 800
5. Fútbol
6. Natación
7. 4 personas
8. 4 personas
Capítulo 14 · Lección 1
Página 250
1. Sí, respuesta abierta
Página 251
2. Ver cuaderno del estudiante
3. En películas
4. Espectáculo en vivo
5. Respuesta abierta
6. Ver cuaderno del estudiante
7. Subsidios de gobierno
8. Contribuciones privadas
9. Suspenso y Ciencia ficción
10. 136 personas por romance, 64 por
comedia, 84 por acción, 52 por
ciencia ficción y 36 por suspenso
11. Respuesta abierta
12. Suspenso
13. Con información de dos conjuntos
de datos y compararlos
14. Contribuciones privadas
15. Comedia
Capítulo 14 · Lección 2
Página 253
1. Ver cuaderno del estudiante
2. 8 días
3. 25
4. 1, porque hay una x en los 30°
5. 30°. Respuesta abierta
6. 16
7. [7 – 15]
8. Sí, 15
9. Ver cuaderno del estudiante
10. Diagrama de tallo y hojas
11. 9 años
12. 15
13. 33
14. Aquella que puede usarse para
mostrar cuántas veces aparece
cada valor de datos](https://image.slidesharecdn.com/libromat6-141102190941-conversion-gate02/85/Libro-mat-6-322-320.jpg)



