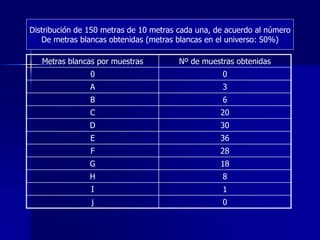
Este documento define estadística y describe sus usos y métodos. Explica que la estadística estudia la recolección y análisis de datos numéricos. Se divide en estadística descriptiva, analítica e inferencial. También describe el método estadístico y sus etapas, así como los conceptos de universo, muestra, y cómo obtener muestras representativas para realizar estudios estadísticos.

1. UNIVERSIDAD NACIONAL EXPERIMENTAL
“FRANCISCO DE MIRANDA”
ADI
UNIDAD CURRICULAR: TRABAJO COMUNITARIO 2
ESTADISTICA
PROF: Dra. Marina Ávila

2. ESTADISTICA:
Tiene 2 significados diferentes:
 En plural: sinónimo de datos numéricos, es decir,
es un método
 En Singular: método utilizado en el manejo de los
datos numéricos, es decir el método de recolectar,
elaborar e interpretar datos numéricos.

3. Estadística como:
Ciencia: Que estudia la
recolección, clasificación
y presentación de los hechos,
Sujetos a la apreciación numérica
Método: Apto para recolectar,
Elaborar, analizar e interpretar
Datos numéricos
Técnica: ayuda a la ciencia a trabajar,
Con material cualitativo y cuantitativo

4. Usos de la Estadística:
1. Se emplea en el estudio de grandes poblaciones
2. Se usa en el estudio de fenómenos cuantitativos y cualitativos
3. Al realizar el Dx de un estado patológico, o el examen al Px
a través de los signos y síntomas.
4. Al estudiar los resul. de exámenes de Lb. y considerar los
valores normales y patológicos.
5. Al elaborar encuestas epidemiológicas y observar las bondades de
la vacunación.
6. Para elaborar el perfil de una región, tomando en consideración los
índices utilizados en salud.

5. BASE DE LA ESTADISTICA
 Se fundamenta en la variación de los fenómenos y
de las observaciones. Consta de un componente
real y uno falso
 El componente real, es inherente a todos los individuos.
 El componente falso, viene dado por factores
sobreañadidos

6. CLASIFICACIÓN DE LA ESTADISTICA
1. Según el tipo de análisis:
 Estadística General: Estudia en forma racional y
sistemática los procesos numéricos descriptivos e
inductivos, comunes a todos los campos de la
investigación científica.
 Estadística aplicada: Es la estadística referida a
determinados campos de la investigación. Ejm.
Demografía, Biometría.

7. 2. Según los fines del estudio:
2.1 Estadística Descriptiva: Se ocupa de la recolección, clasificación,
ordenación, tabulaciones y representaciones gráficas de los datos
estadísticos que se deriven de la medición de las características
objetos de estudio.
2.2 Estadística Analítica: Consiste en el análisis de la información a
partir de los datos estadísticos disponibles, partiendo de medidas
estadísticas simples (promedio, mediana) las medidas de
correlación, hasta los más complejos, tanto en el campo
univariante como multivariante
2.3 Estadística Inferencial: es la que propone obtener conclusiones
válidas del conjunto en es estudio (Población, Universo) a partir
del análisis de subconjuntos representativos (Muestras)

8. ESTUDIO ESTADISTICO
Es el que se realiza con datos numéricos y
utilizando el método.
 Clasificación del estudio estadístico:
1. Según su procedimiento
Longitudinal: Estudio
Continuo, seriado. Ejm:
Los registros
Transversal: Estudio que
se realiza en un momento
dado (censos)

9. 2. Según el análisis o propósito:
3. Según el tiempo.
Descriptivo. Describe las
características principales
del estudio
Inductivo: relacionaos
Con las poblaciones
Prospectivo
Retrospectivo Actual

10.  MÉTODO ESTADÍSTICO Y MÉTODO CIENTÍFICO

11.  Etapas del método científico:
1. Exacta observación del fenómeno que se
estudia.
2. Formulación de una hipótesis, mediante
la cual puedan explicarse los hechos
observados.
3. Verificación de la hipótesis mediante
nuevas observaciones.

12. El Método Estadístico
1. El Método Estadístico interviene en el primer paso
de la investigación científica ayudando a que las
observaciones sean fidedignas y exactas.
2. En la Verificación de la hipótesis. Como la
verificación de las hipótesis se hace siempre
mediante nuevas observaciones, es necesario poder
resumir adecuadamente los resultados de éstas
3. al resumir convenientemente el resultado de las
observaciones, facilita el razonamiento y pone
presente relaciones que pueden conducir a la
formulación de hipótesis racionales.

13. ETAPAS DE MÉTODO ESTADÍSTICO
 La aplicación de la estadística a un problema determinado
comprende las siguientes 4 etapas:
1. Planificación del estudio.
2. Recolección de la información.
3. Elaboración de los datos recogidos.
4. Análisis e Interpretación.

14. ETAPA DE PLANIFICACIÓN
1. Cuando intentamos realizar un estudio, comenzamos por
hacer un Planteamiento del Problema en el cual estamos
interesados.
2. Búsqueda y Evaluación de la Información ya existente, lo
cual nos llevará a su mejor conocimiento, nos enseñará
nuevas técnicas y complementará nuestra previa
experiencia, pero a la vez nos pondrá presentes un
conjunto de fallas en nuestros conocimientos que conducirá
3. Formulación de Hipótesis
4. Verificación de las Hipótesis
5. Conclusiones y Recomendaciones.

15. Relaciones entre el Método Estadístico y la Medicina.
 Tiene gran utilidad para el investigador médico que
trata de probar una hipótesis de trabajo que
pretende simplemente extraer ciertas conclusiones
de las observaciones realizadas.
 El estudiante le permite evaluar más objetivamente
la evidencia que otros investigadores le presentan.

16. USOS DE LA ESTADÍSTICA EN MEDICINA INDIVIDUAL
 En el campo de la clínica, al diagnóstico de cualquier
enfermedad sólo es posible llegar mediante la experiencia
ganada a través del análisis estadístico de un conjunto de
síntomas y signos observados en muchos individuos. Si
decimos por ejemplo, que el signo de Koplick sólo se presenta
en el Sarampión
 Un pronóstico a su vez, no es otra cosa que la aplicación del
cálculo de probabilidades a un enfermo determinado.
 Finalmente, todo nuevo tratamiento requiere un ensayo
experimental que demuestre si es realmente efectivo e
inocuo.

17. USOS DE LA ESTADÍSTICA EN MEDICINA COLECTIVA
 En el campo de la Salud Pública, sólo mediante
procedimientos estadísticos podrá conocerse la composición y
Principales características de la población que se van a servir,
los cambios que acontecen en ella los riesgos a que está
sometida y las necesidades que presenta.
 La planificación de la actividades de Salud Pública, el control
de los programas que se estén desarrollando y la actividad
final de sus rendimientos y eficiencia sólo podrá llevarse a
cabo mediante procedimientos Estadísticos.

18. UNIVERSO Y MUESTRAS

19. UNIVERSO Y MUESTRAS
 UNIVERSO o POBLACIÓN la totalidad de individuos o
elementos en los cuales puede presentarse determinada
característica susceptible de ser estudiada.
 MUESTRA a su vez, es una parte o grupo del universo.
 Ejemplo si con el fin de conocer la estatura media de los
5.000 alumnos de la escuela de medicina escogemos un
grupo representativo de 500 de ellos, el universo en
estudio estará formado por la totalidad de los 5.000, y la
muestra consistirá de los 500 escogidos.

20. Los universos pueden ser finitos e infinitos.
 El universo se denomina finito, cuando está formado
por un número limitado de unidades, como sería el
número de alumnos de la Universidad, de médicos en
Venezuela, entre otros.
 Se denomina infinito, cuando cuenta con un número
ilimitado de unidades: el número de estrellas en el
cielo, de insectos en la naturaleza, entre., son
universos infinitos que nunca podrán ser
cuantificados. En ocasiones, el universo que se
estudia puede ser hipotético y entonces se le
considera como infinito.

21. VENTAJAS DEL EMPLEO DE MUESTRAS
 Ahorra tiempo, dinero y trabajo.
 Permite una gran exactitud en el
estudio.

22. DESVENTAJAS DEL EMPLEO DE MUESTRAS
 Única desventaja, es el error de muestreo, el cual sumando a
los 3 tipos de errores antes mencionados, podría invalidar
nuestro estudio.
 Este error por muestreo es una constancia de la variabilidad
de las poblaciones.
 Ejm. Con el fin de aclarar el anterior concepto,
supongamos una población de 4 personas que tuvieran
respectivamente 5, 3, 2 y 10 bolívares.
 El error por muestreo suele ser mucho menos importantes
que los errores debidos al observador, al método de
observación y a los individuos estudiados, y en segundo lugar,
que el error por muestreo puede medirse estadísticamente y
en cierto modo, puede disminuirse a voluntad, tan solo con
aumentar el tamaño de la muestra.

23. CONDICIONES DE UNA BUENA MUESTRA
 Las condiciones que una muestra deben tener
para que sea «buena», es decir para que
rinda la mayor utilidad posible, son dos. La
muestra debe ser adecuada en:
 a. Cantidad
 b. Calidad

24. CANTIDAD DE INDIVIDUOS EN LA MUESTRA
 El que una muestra sea buena en CANTIDAD, quiere decir
que debe incluir un número óptimo y mínimo de individuos.
Hay fórmulas estadísticas mediante las cuales podemos
calcular el número de individuos que debemos incluir en cada
investigación.
El número de individuos que deben incluirse en la muestra,
depende, entre otros de 2 factores, a saber:
a. La fr. con la cual en fenómeno que se estudia se encuentra
en el universo. Si una enfermedad representa tan solo en el
1% de la población.
b. La variabilidad del universo que se estudia.

25. CALIDAD DE LA MUESTRA
 El que una muestra sea buena en CALIDAD debe reflejar
fielmente las características del universo del cual procede y
diferir de él sólo en el número de unidades incluidas.
 Los aspectos referentes a la calidad de la muestra, son
más importantes que los referentes a su cantidad y no
debe pensarse que la calidad de la muestra depende de su
cantidad.
Si queremos estudiar las características del pueblo
Venezolano, y se estudia a los habitantes de Mérida,
aunque estudiaríamos a todos ellos, nuestra muestra no
sería representativa de todo el país.

26. MUESTRAS REPRESENTATIVAS Y MUESTRAS SELECCIONADAS
 Quiere decir que si queremos generalizar que lo que es cierto
en la muestra es cierto también en todo el universo, entonces
la muestra debe ser perfectamente representativa en él.
 Muestra no es representativa de su universo, se dice que es
una muestra «seleccionada» y generalmente no es
conveniente trabajar con tales muestras.
 La selección puede ser voluntaria o involuntaria.
Voluntaria: el investigador conoce las limitaciones del
material que está estudiando y las conclusiones que derive
debe estar de acuerdo con ellas. Un investigador, por ejemplo
que estudie las variaciones del peso de un grupo de escolares
de 8 años, no podrá generalizar sus hallazgos a escolares de
todas las edades sino exclusivamente al grupo de edad
investigado

27. La involuntaria: es más importante, porque a menudo se ignora dicha
selección, se prenderá generalizar a toda una población, conclusiones
que no le corresponden.
Generalmente este error se comete por una de las 3 causas siguientes:
a. Porque se toma la muestra de un sector del universo, creyendo
equivocadamente que dicho sector constituye todo el universo.
b. Porque el método de escogencia de los individuos no es el azar, el cual
como veremos enseguida es el único procedimiento que nos garantiza
un buena escogencia. Tal error se comete siempre que se trabaja con
muestras de conveniencia
c. Porque una vez obtenida la muestra, existen circunstancias que nos
impide estudiar a los individuos escogidos. La muestra puede haber
sido escogida de toda la población y por un procedimiento al azar, con
lo cual se eliminan las 2 causas de error acabadas de estudiar, pero si
no es posible escoger la información de las personas que deben
estudiarse, ciertos segmentos de la población no van a quedar
representados.

29. TIPOS DE MUESTRAS
Hay dos clases de muestras:
a. Muestras de Conveniencia.
b. Muestras Probabilísticas.

30. MUESTRAS DE CONVENIENCIA
• Son todas aquellas muestras en las cuales, los individuos se
escogen con base en la opinión de un experto por
considerarlos representantes típicos del universo que se
quiera conocer, sin embargo la validez de los resultados
obtenidos dependerá exclusivamente del acierto que se tenga
al seleccionar como típica dicha muestra.
 Desventaja: aun cuando los resultados pueden ser bastante
fidedignos, existe la incapacidad de juzgar objetivamente
sobre su precisión.

31. MUESTRAS PROBABILÍSTICAS
 Son aquellas en que cada individuo de la población tiene
una probabilidad perfectamente conocida de ser incluido en
la muestra. No es ni siquiera necesario que los diferentes
individuos tengan un igual chance de pertenecer a la
muestra, basta con que tengan cualquier posibilidad
(diferente de cero) de formar parte de ella y que esa
probabilidad sea conocida.
 Condiciones para elegir una muestra probabilística:
1. Que la probabilidad de elegir a cada individuo sea
perfectamente conocida
2. Es indispensable que los individuos se elijan al azar, sin
permitir la intervención de ningún factor voluntario que
favorezca la elección.

32. Metras blancas por muestras Nº de muestras obtenidas
0 0
A 3
B 6
C 20
D 30
E 36
F 28
G 18
H 8
I 1
j 0
Distribución de 150 metras de 10 metras cada una, de acuerdo al número
De metras blancas obtenidas (metras blancas en el universo: 50%)

33. 1. Hay cierta variación en los resultados obtenidos
con las muestras
2. La causa de la variación fue al azar
3. A pesar de la variación presente, puede
observarse que no todos los resultados se
presentan con la misma frecuencia
4. Puede observarse que los resultados no son
desordenados, sino que presentan cierta simetría.

34. ELECCIÓN ENTRE MUESTRAS
PROBABILÍSTICAS Y DE CONVENIENCIA
 la diferencia de la muestra de conveniencia con la
probabilística es que la posibilidad de que un
individuo sea incluido en la muestra es
desconocida, siendo imposible medir la exactitud de
los resultados obtenidos.
 A causa de esto, siempre que sea posible deben
utilizarse muestras probabilísticas, a pesar de que
hay ocasiones en las cuales se precisa recurrir a
muestras de conveniencia.

35. a. Por limitaciones en recursos, se tiene que estudiar un número
de individuos menor que el fuera deseable y entonces la
opinión de un experto puede ser conveniente.
b. No se puede obtener una lista completa de la población que se
va a estudiar, siendo por lo tanto imposible aplicar el azar.
c. Hay ocasiones en las cuales el principal interés esta en
localizar individuos con determinadas características con una
población muy numerosa, digamos los enfermos tuberculosos
de una colectividad.
ocasiones en las cuales se precisa recurrir a
muestras de conveniencia.

36. MÉTODOS PARA LA OBTENCIÓN DE UNA
MUESTRA PROBABILÍSTICA
 Básicamente son dos los métodos para asegurar la
escogencia de una nueva muestra:
a. El método de la lotería.
b. El método de los números al azar.
 El método de la lotería consiste en colocar en un
recipiente fichas con los nombres de todos los
integrantes de la población que se va a estudiar y
después de revolverlas bien, se extraerán tantas
fichas como individuos se quieran obtener. Se
comprende que si la población es muy numerosa
este procedimiento resulta poco práctico.

37.  Las tablas de números al azar son tablas con miles de
números obtenidos por un procedimiento como el de la lotería
(azar). Los números están agrupados en bloques de 5 x 5,
esta distribución se hace simplemente con el fin de facilitar la
lectura, siendo indiferente que ésta se realice hacia abajo,
hacia arriba, horizontal o diagonalmente.
 Para utilizar estas tablas se empieza por numerar a los
individuos de la población desde el 1 en adelante y luego se
extraerán tantos números como individuos vayan a incluirse
en la muestra.
 La tabla puede empezarse a leer en cualquier parte, pero
debe escogerse al azar la columna y fila de comienzo, para lo
cual es suficiente colocar a ciegas un dedo sobre el cuerpo de
la tabla y empezar desde ese sitio la lectura.

38. DIFERENTES TIPOS DE MUESTRAS
PROBABILISTICAS
1. Muestras por azar simple
2. Muestras sistemáticas
3. Muestras estratificadas
4. Muestras de conglomerado
5. Muestras por procedimiento combinado

39. 1. Muestras por azar simple.
Tiene 3 inconvenientes
a) Se necesita una lista detallada de todos los
individuos de la población en estudio
b) La muestra quedara dispersa
c) No hay garantía que las distintas poblaciones
estén adecuadamente representadas en la
muestra

40. 2. Muestras sistemáticas
Para obtener este tipo de muestra, se debe tener
una lista de toda la población en estudio (todos
los estudiantes del País) y se numeran del 1 al
20000, luego se escogerá al azar un Nº entre 1 y
10 que indica el Nº que entra en el estudio.
Sin embargo, si la lista no esta hecha al azar la
utilización de este tipo de muestra puede
conducir a serios errores

41. 3. Muestras estratificadas.
 En este sistema la población se divide en
“estratos o sectores y luego cada uno de los
estratos se escogerán al azar los individuos que
formaran la muestra.
 Se requiere igualmente una lista detallada.
 La ventaja sobre el muestreo por azar simple:
a) Se obtiene información separada para cada uno
de los estratos
b) Se evita el riesgo que determinado estrato o
sector quede inadecuadamente representada

42. 4. Muestras de conglomerado:
Se escogen grupos o conglomerados de individuos.
 No se necesita tener una lista detallada de los
individuos
 Se evita dispersión
 El único inconveniente pudiera ser que las zonas
no quedaran adecuadamente representadas
 No dan resultados tan precisos como los
obtenidos con las estratificadas

43. 5. Muestras por procedimiento combinado:
 Las muestras por conglomerado evitan la
necesidad de tener una lista detallada de la
totalidad el universo que se estudia y evitan la
dispersión de la muestra, y a la vez la muestras
estratificadas aseguran la representabilidad de los
diferentes sectores de la población, una
combinación de los 2 sistemas elimina los
grandes inconvenientes del muestreo por azar
simple

44. ANÁLISIS DE RESULTADOS DE LA MUESTRA
 Una vez obtenida la muestra y convenientemente
resumidos los hallazgos, el paso siguiente es la
generalización de los resultados a la población a la
cual procede. Dicha generalización exige 2
requisitos:
 Estimar los valores del universo, y
 Juzgar sobre la representación de tales valores.

45. La estimación de los valores de universo depende del tipo de
muestra que se haya utilizado.
1. VALORES DE UNIVERSO
 Cuando se trata de una muestra por azar simple o de un
muestra sistemática, los resultados observados en ella
pueden aplicarse directamente al universo.
 Cuando la muestra es estratificada o de conglomerados, se
resumirán en primer lugar los resultados de cada estrato o
conglomerado y luego se estimará el valor global de todo el
universo lo cual requiere la utilización de los llamados
promedios ponderados.
 En caso de las muestras por procedimiento combinado es
más complicado. Se aconseja el asesoramiento de un
técnico estadístico

46. 2. PRECISION DE LOS RESULTADOS
 Si en la muestra estudiada se encontró que el 40% de los
escolares son mujeres podemos aplicar tal porcentaje a la
totalidad de la población escolar de Venezuela (solo una
aproximación).
 Siempre que se hacen generalizaciones a partir de una
muestra, se corre el riesgo de que los valores dados por ella
no correspondan exactamente a los del universo. Sin
embargo, el riesgo puede reducirse y estimarse con bastante
exactitud a partir de los propios resultados de la muestra, a
condición de que sea una muestra probabilística, y que su
tamaño sea adecuado.