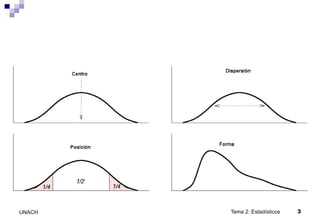
Este documento presenta una introducción a los conceptos básicos de estadística descriptiva, incluyendo parámetros, estadísticos, medidas de posición (media, mediana, moda), medidas de dispersión (rango, desviación estándar) y diagramas de cajas. Explica que los parámetros se calculan sobre poblaciones mientras que los estadísticos se calculan sobre muestras, y que los estadísticos pueden usarse para estimar parámetros. También define y contrasta diferentes medidas de tendencia central y dispersión.















![Tema 2: Estadísticos 17
UNACH
0,5 58
0,75 5
60 – 70
70 - 80
Peso M. Clase Fr. Fr. ac.
40 – 50 45 5 5
50 – 60 55 10 15
65 21 36
75 11 47
80 - 90 85 5 52
90 - 100 95 3 55
100 – 130 115 3 58
Ejemplo (continuación)
x
∑i
xi ni
n
45⋅5 55⋅10 115⋅3
58
69,3
Mediana C0,5 Li−1
⋅ − Ni−1
ni
(Li
−Li−1)
60
58
0,5⋅58−15
21
(70− 60)
66,6
P75 C0,75 Li−1
⋅ 8−
ni
Ni−1
(Li
− Li−1) 70
43,5−36
(80 − 70)
11
76,8
Moda = marca de clase de (60,70] = 65
Cada libro ofrece una fórmula diferente para la moda (difícil estar al día.)](https://image.slidesharecdn.com/estadisticaunach02descriptiva-230208222608-7e996375/85/estadistica_Descriptiva-doc-17-320.jpg)











