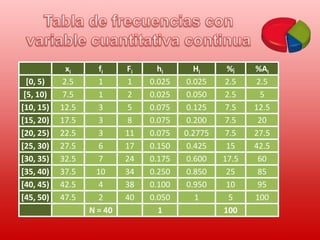
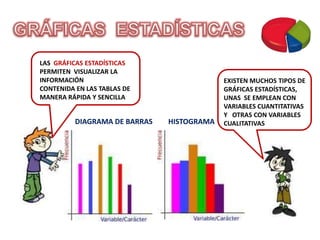
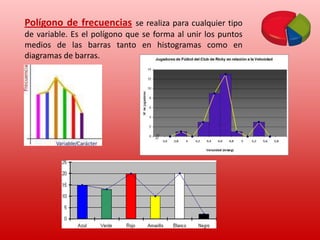
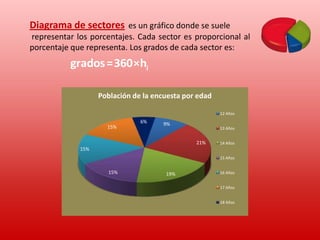
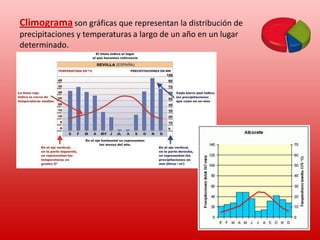
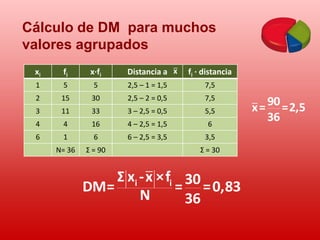
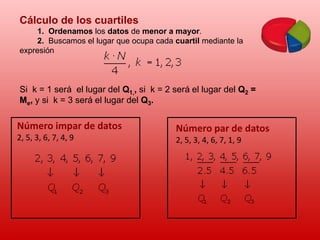
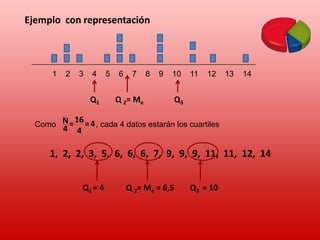
Este documento describe conceptos básicos de estadística. Explica que la estadística se utiliza para recopilar, organizar y analizar datos para sacar conclusiones. Luego detalla las cuatro etapas de un estudio estadístico: recopilación de datos, organización de datos, análisis de datos y obtención de conclusiones. Finalmente, define términos estadísticos clave como población, muestra, variable, valor y proporciona ejemplos de cómo organizar y representar datos estadísticos.

1. Estadística2º ESO

2. La Estadística trata del recuento, la ordenación y clasificación de datos obtenidos por las observaciones, para poder hacer comparaciones y sacar conclusiones. Un estudio estadístico consta de las siguientes fases: Recogida de datos

3. Organización y representación de datos

4. Análisis de datos

5. Obtención de conclusionesConceptosPoblaciónes el conjunto de elementos sobre los cuales se va a estudiar una determinada característica.Muestraes una parte de la población.Variable estadística: el aspecto que se va a estudiar. Si se puede medir se llama variable cuantitativa si no se pueden medir se llama variable cualitativa.Si la variable estadística toma un número determinado de valores se llama variable discreta.Si la variable estadística puede tomar cualquier valor entre dos valores dados se llamavariable continua.Valor es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico.

6. PASO 1:RECOGIDA DE DATOS :Planteado el test o encuesta oportuno , una vez elegido el tema al que se quiere hacer el estudio estadístico, y recogidos los datos que correspondan, el primer análisis que realizaremos es el del tipo de variable que pretendemos estudiar (Cualitativa o Cuantitativa; Discreta o Continua). Esto condicionará en gran medida su posterior tratamiento.

7. PASO 2:ORGANIZACIÓN DE LOS DATOS :Determinado el modo de agrupamiento de las observaciones, procedemos a su recuento,construyendo la tabla de frecuencias. Posteriormente podremos visualizar tales frecuencias de forma gráfica con el diagrama estadístico apropiado.TABLA DE FRECUENCIASGRÁFICOS: diagrama de barras, histograma, polígono de frecuencias, diagrama de sectores, pictogramas, pirámides de población, climogramas, etc.

8. Recuento

9. Tabla de frecuenciasTabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente. Frecuencia absolutaes el número de veces que aparece un determinado valor en un estudio estadístico. Se representa por fi. La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N. Frecuencia relativadecimales el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos. Se representa por hi. La suma de las frecuencias relativas decimales es igual a 1.

10. Frecuencia relativa porcentual es la frecuencia relativa decimal multiplicada por 100. Se puede expresar por %i La suma de las frecuencias relativas porcentuales es 100.Frecuencias acumuladas es la suma de las frecuencias correspondientes de todos los valores inferiores o iguales al valor considerado. Se representa por:Fi la frecuencia absoluta acumulada Hi la frecuencia relativa decimal acumulada%Ai la frecuencia relativa porcentual acumuladaPara que tengan sentido los frecuencias acumuladas, los valores de la variable deben estar ordenados.

11. Tabla de frecuencias con variable cuantitativa discreta

12. Tabla de frecuencias con variable cuantitativa continua

13. GRÁFICAS ESTADÍSTICASLAS GRÁFICAS ESTADÍSTICAS PERMITEN VISUALIZAR LA INFORMACIÓNCONTENIDA EN LAS TABLAS DE MANERA RÁPIDA Y SENCILLAEXISTEN MUCHOS TIPOS DE GRÁFICAS ESTADÍSTICAS, UNAS SE EMPLEAN CON VARIABLES CUANTITATIVASY OTRAS CON VARIABLES CUALITATIVASDIAGRAMA DE BARRASHISTOGRAMA

14. Diagrama de barras se utiliza para de presentar datos cualitativos o datos cuantitativos de tipo discreto.Se representan sobre unos ejes de coordenadas, en el eje de abscisas se colocan los valores de la variable, y sobre el eje de ordenadas las frecuencias absolutas, relativas, porcentajes o frecuencias acumuladas. Los datos se representan mediante barras de una altura proporcional a la frecuencia.

16. Histogramase utiliza para de presentar datos cuantitativos de tipo continuo.Se representan sobre unos ejes de coordenadas, en el eje de abscisas se colocan los intervalos de los valores de la variable, y sobre el eje de ordenadas las frecuencias absolutas, relativas , porcentajes o frecuencias acumuladas. Los datos se representan mediante barras pegadas unas a otras de una altura proporcional a la frecuencia.

17. Polígono de frecuenciasse realiza para cualquier tipo de variable. Es el polígono que se forma al unir los puntos medios de las barras tanto en histogramas como en diagramas de barras.

18. Diagrama de sectoreses un gráfico donde se suele representar los porcentajes. Cada sector es proporcional al porcentaje que representa. Los grados de cada sector es:

19. Pictogramaes un gráfico con figuras

20. Pirámide de poblaciónconsiste en dos histogramas, uno para hombres y otro para mujeres, correspondientes a habitantes de una misma comunidad más o menos extensa, repartidos por edades.Es útil para estudiar su situación demográfica y buscar explicaciones a situaciones presentes , pasadas y futuras.

21. Climogramason gráficas que representan la distribución de precipitaciones y temperaturasa largo de un año en un lugar determinado.

22. PASO 3:ANÁLISIS DE DATOS: Para este análisis se utilizan los parámetros estadísticos:Medidas de centralización MEDIA, MEDIANA y MODA Medidas de dispersión RECORRIDO, DESVIACIÓN MEDIA,….c) Medidas de posición PERCENTILES y CUARTILES

23. Medidas de centralizaciónMEDIA ARITMÉTICA, MODA, MEDIANAMEDIA ARITMÉTICAes el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.Si los datos vienen agrupados en una tabla de frecuencias, la expresión de la media es:Evidentemente esta medida sólo se puede hallar para variables cuantitativas.

24. Ejemplo de cálculo de media:En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media

25. MODAes el valor que tiene mayor frecuencia absoluta.Se representa por Mo.Se puede hallar para cualquier tipo de variable, aunque para variables cuantitativas es poco útil.La moda de la distribución: 2, 3, 3, 4, 4, 4, 5, 5 es Mo= 4 Si en un grupo hay dos o varias puntuaciones con la misma frecuencia y esa frecuencia es la máxima, la distribución es bimodal o multimodal, es decir, tiene varias modas. 1, 1, 1, 4, 4, 5, 5, 5, 7, 8, 9, 9, 9 Mo= 1, 5, 9

26. MEDIANA es el valor que ocupa el lugar central de todos los datos cuando éstos están ordenados de menor a mayor. La mediana se representa por Me.La mediana se puede hallar sólo para variables cuantitativas.Cálculo de la mediana con pocos datosOrdenamos los datos de menor a mayor. Si la serie tiene un número impar de medidas la mediana es la puntuación central de la misma. 2, 3, 4, 4, 5, 5, 5, 6, 6 Me= 5Si la serie tiene un número par de puntuaciones la mediana es la media entre las dos puntuaciones centrales. 7, 8, 9, 10, 11, 12 Me= 9.5

27. Cálculo de la mediana para datos agrupadosSe divide N entre dos para ver dónde está el centro 104/2 = 52Se busca en la columna de Fi dónde estaría 52.Luego el valor o intervalo mediano será:Clase de la mediana: [66, 69)

28. RELACIÓN ENTRE MEDIA Y MEDIANASi , la distribución es completamentesimétricaSi los valores de y son próximos, la distribución es aproximadamentesimétricaSi los valores de y son poco próximos, la distribución es asimétrica

29. ACTIVIDAD 1a) A partir de las siguientes gráficas realiza la tabla de frecuencias y calcula MEDIA, MEDIANA y MODA de cada una de las distribuciones.b) Indica tipo de variable y tipo de gráfico en cada caso.c) Indica cómo es simétricamente cada una de ellas.

30. ACTIVIDAD 2En el comedor de un instituto se da a elegir a su alumnado entre varios primeros platos. El resultado de las distintas elecciones nos lo da el siguiente gráfico.a) Indica tipo de variable, y tipo de gráfica.b) Sabiendo que se le ha preguntado a 240 personas, realiza la tablade frecuencias y calcula las medidas de centralización que mássentido tengan.

31. ACTIVIDAD 3Halla la media y mediana de las siguientes distribuciones. Utiliza los resultados para dilucidar si son más o menos simétricas. Después, represéntalas y comprueba. A: 1, 2, 2, 4, 5, 6, 7, 9, 9, 9, 9, 9, 10, 10, 10, 10 B: 1, 1, 1, 2, 2, 3, 4, 5, 6, 6, 7, 7, 8, 9, 9, 9

32. Medidas de dispersión RECORRIDO, DESVIACIÓN MEDIA,….RECORRIDO es la diferencia entre los valores extremos, es decir, entre el mayor valor y el menorRECORRIDO = Valor mayor - Menor valorDESVIACIÓN MEDIAes un parámetro asociado a la media; y es el promedio ( o media) de las distancias de los valores de todos los individuosa la media.Para muchos valores y agrupadosLas medidas de dispersión sirven para comparar dos o más distribuciones y decidir cuál de ellas es más o menos dispersa

33. Cálculo de DM para pocos valoresDistribución 5, 7, 8, 9, 11, 13, 13, 15, 16, 18SUMA35

34. Cálculo de DM para muchos valores agrupados

35. ACTIVIDAD 4Halla la y la DM de las siguientes distribuciones. Represéntalas y compara. a) b)

36. Medidas de posición CUARTILES, PERCENTILES, ….CUARTILES son los tres valores de la variable que dividen a un conjunto de datos ordenados en cuatro partes iguales.Q1, Q2 y Q3 determinan los valores correspondientes al 25%, al 50% y al 75% de los datos.Por tanto Q2 coincide con la mediana.Q1 : cuartil inferior. Entre Q1 y Me = Q2 está un 25 % de la población.Q3 : cuartil superior. Entre Me = Q2 y Q3 está un 25 % de la población.

37. Cálculo de los cuartiles1. Ordenamos los datos de menor a mayor. 2. Buscamos el lugar que ocupa cada cuartil mediante la expresión Si k = 1 será el lugar del Q1,, si k = 2 será el lugar del Q2 = Me, y si k = 3 será el lugar del Q3.Número impar de datos2, 5, 3, 6, 7, 4, 9Número par de datos2, 5, 3, 4, 6, 7, 1, 9

38. Ejemplo con representación1 2 3 4 5 6 7 8 9 10 11 12 13 14Q1 Q 2= Me Q3Como , cada 4 datos estarán los cuartiles1, 2, 2, 3, 5, 6, 6, 6, 7, 9, 9, 9, 11, 11, 12, 14Q1 = 4 Q 2= Me = 6,5 Q3 = 10

39. ACTIVIDAD 5En cada una de las siguientes distribuciones:Halla Q1 ,Q 2= Me y Q3 .Representa los datos y sitúa Q1, Q 2= Me y Q3 sobre ellos. A: 1, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 6, 7, 8, 9, 10 B: 1, 3, 3, 4, 5, 5, 6, 7, 8, 8, 9, 10, 11, 11, 12, 12, 13, 16

40. PERCENTILES son los valores de la variable que dividen a un conjunto de datos ordenados en cien partes iguales.Los percentiles se representan por: P10, P20, P30, P40, P50 = Me = Q2, P60, P70, P80, P90, P100Así por ejemplo: P1 es el valor que deja a la izquierda el 1 % de datos, y a la derecha el 99 % de datos...............P10 es el valor que deja a la izquierda el 10 % de datos, y a la derecha el 90 % de datos.……………P60 es el valor que deja a la izquierda el 60 % de datos y a la derecha el 40 % de datos.