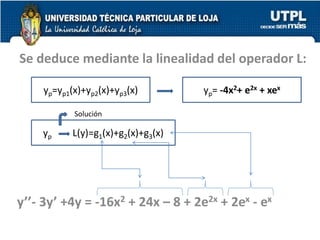
Este documento presenta el Teorema 4.7 sobre el Principio de Superposición para Ecuaciones Diferenciales no Homogéneas. Explica que si yp1, yp2, y yp3 son soluciones particulares de ecuaciones no homogéneas separadas, entonces yp1 + yp2 + yp3 es una solución particular de la ecuación no homogénea combinada. Proporciona un ejemplo numérico para ilustrar esto.

1. Integrantes:
•Marisela Valle
•Gabriela Agila
•Carlos Rojas
•Patricio Jaramillo
•Jorge Ulloa

2. Teorema 4.7
Principio Superposición ENH
Sol.Parti. Supongamos yp1 yp2 yp3
an(x)y(n)+an-1(x)y(n-1)+……….+a1(x)y’+a0(x)y=gi(x),
donde i=1,2,……..,k. Que corresponde a k gi(x), g2(x), g3(x), Entonces
yp=yp1(x)+yp2(x)+………+ypk(x)
Es una solución particular de
an(x)y(n)+an-1(x)y(n-1)+……….+a1(x)y’+a0(x)y
=g1(x)+g2(x)+………+gk(x).

3. DEMOSTRACIÓN
Caso k=2
yp1(x) yp2(x) Soluciones Particulares
L(y)=g1(x) L(y)=g2(x) ED no Homogénea
Demostración
yp=yp1(x)+yp2(x)
Yp L(y)=g1(x)+g2(x)
Solución

4. Se deduce mediante la linealidad del operador L:
Demostración
L(yp) = L{yp1(x)+yp2(x)}
= L(yp1(x))+L(yp2(x))
= g1(x)+g2(x) //
yp=yp1(x)+yp2(x)
Yp L(y)=g1(x)+g2(x)
Solución

5. EJEMPLO 11
yp1(-4x2) Solución Particular
y’’-3y’+4y=-16x2 + 24x - 8 ED no Homogénea
yp2(e2x) Solución Particular
y’’-3y’+4y=2e2x ED no Homogénea
yp3(xex) Solución Particular
y’’-3y’+4y=2e2x - e ED no Homogénea

6. Se deduce mediante la linealidad del operador L:
y’’- 3y’ +4y = -16x2 + 24x – 8 + 2e2x + 2ex - ex
yp=yp1(x)+yp2(x)+yp3(x)
yp L(y)=g1(x)+g2(x)+g3(x)
Solución
yp= -4x2+ e2x + xex

7. EJEMPLO 35
yp1(3e2) Solución Particular
y’’-3y’+4y=-16x2 + 24x - 8 ED no Homogénea
yp2(e2x) Solución Particular
y’’-3y’+4y=2e2x ED no Homogénea
yp3(xex) Solución Particular
y’’-3y’+4y=2e2x - e ED no Homogénea