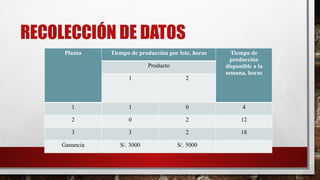
Wyndor Glass Co. busca maximizar sus utilidades mediante la producción de dos nuevos productos de vidrio en tres plantas, enfrentando limitaciones de capacidad. Se ha determinado que la compañía debe fabricar 2 lotes del producto 1 y 6 del producto 2 a la semana, generando una ganancia total de 36,000 soles semanales. Se aplicó un modelo de programación lineal para resolver este problema de producción y optimización.

1. EL PROBLEMA DE LA
WYNDOR GLASS CO.
SOLUCIÓN DE MODELOS DE PROGRAMACIÓN LINEAL CON MÉTODO SIMPLEX

2. DESCRIPCIÓN DE CASO
LA WYNDOR GLASS CO. PRODUCE ARTÍCULOS DE VIDRIO DE ALTA CALIDAD, ENTRE ELLOS
VENTANAS Y PUERTAS DE VIDRIO. TIENE TRES PLANTAS. LOS MARCOS Y MOLDURAS DE
ALUMINIO SE HACEN EN LA PLANTA 1, LOS DE MADERA EN LA PLANTA 2; LA 3 PRODUCE EL
VIDRIO Y ENSAMBLA LOS PRODUCTOS.
DEBIDO A UNA REDUCCIÓN DE LAS GANANCIAS, LA ALTA ADMINISTRACIÓN HA DECIDIDO
REORGANIZAR LA LÍNEA DE PRODUCCIÓN DE LA COMPAÑÍA. SE DESCONTINUARÁN VARIOS
PRODUCTOS NO RENTABLES Y SE DEJARÁ LIBRE UNA PARTE DE LA CAPACIDAD DE PRODUCCIÓN
PARA EMPRENDER LA FABRICACIÓN DE DOS PRODUCTOS NUEVOS QUE TIENEN VENTAS
POTENCIALES GRANDES:
PRODUCTO 1: UNA PUERTA DE VIDRIO DE 3 METROS CON MARCO DE ALUMINIO.
PRODUCTO 2: UNA VENTANA CORREDIZA CON MARCO DE MADERA DE 4 M X 2M.

3. DESCRIPCIÓN DE CASO
EL PRODUCTO 1 REQUIERE PARTE DE LA CAPACIDAD DE PRODUCCIÓN EN LAS
PLANTAS 1 Y 3 Y NADA EN LA PLANTA 2. EL PRODUCTO 2 SÓLO NECESITA TRABAJO
EN LAS PLANTAS 2 Y 3. LA DIVISIÓN DE COMERCIALIZACIÓN HA CONCLUIDO QUE LA
COMPAÑÍA PUEDE VENDER TODOS LOS PRODUCTOS QUE SE PUEDAN FABRICAR
EN LAS PLANTAS. SIN EMBARGO, COMO AMBOS PRODUCTOS COMPETIRÍAN POR LA
MISMA CAPACIDAD DE PRODUCCIÓN EN LA PLANTA 3, NO ESTÁ CLARO QUÉ
MEZCLA DE PRODUCTOS SERÍA LA MÁS RENTABLE. POR LO TANTO, SE HA
FORMADO UN EQUIPO DE INVESTIGACIÓN PARA ESTUDIAR ESTE PROBLEMA.

4. DESCRIPCIÓN DE CASO
EL GRUPO COMENZÓ POR ANALIZAR JUNTAS CON LA ALTA ADMINISTRACIÓN PARA IDENTIFICAR
LOS OBJETIVOS DEL ESTUDIO Y DESARROLLARON LA SIGUIENTE DEFINICIÓN DEL PROBLEMA:
DETERMINAR QUÉ TASAS DE PRODUCCIÓN DEBEN TENER LOS DOS PRODUCTOS CON EL FIN DE
MAXIMIZAR LAS UTILIDADES TOTALES, SUJETAS A LAS RESTRICCIONES IMPUESTAS POR LAS
CAPACIDADES DE PRODUCCIÓN LIMITADAS DISPONIBLES EN LAS TRES PLANTAS. (CADA
PRODUCTO SE FABRICARÁ EN LOTES DE 20 UNIDADES, DE MANERA QUE LA TASA DE
PRODUCCIÓN ESTÁ DEFINIDA COMO EL NÚMERO DE LOTES QUE SE PRODUCEN A LA SEMANA).
SE PERMITE CUALQUIER COMBINACIÓN DE TASAS QUE SATISFAGA ESTAS RESTRICCIONES,
INCLUSO NO FABRICAR UNO DE LOS PRODUCTOS Y ELABORAR TODO LO QUE SEA POSIBLE
DEL OTRO.

5. DESCRIPCIÓN DE CASO
EL EQUIPO DE INVESTIGACIÓN IDENTIFICÓ LOS DATOS QUE SE NECESITABA REUNIR:
1. NÚMERO DE HORAS DE PRODUCCIÓN DISPONIBLES POR SEMANA EN CADA
PLANTA PARA ESTOS NUEVOS PRODUCTOS. (CASI TODO EL TIEMPO DE ESTAS
PLANTAS ESTÁ COMPROMETIDO CON LOS NUEVOS PRODUCTOS ACTUALES, LO
QUE LIMITA LA CAPACIDAD PARA MANUFACTURAR NUEVOS PRODUCTOS).
2. NÚMERO DE HORAS DE FABRICACIÓN QUE EMPLEA CADA LOTE PRODUCIDO DE
CADA ARTÍCULO NUEVO EN CADA UNA DE LAS PLANTAS.
3. LA GANANCIA POR LOTE DE CADA PRODUCTO NUEVO.

6. RECOLECCIÓN DE DATOS
Planta Tiempo de producción por lote, horas Tiempo de
producción
disponible a la
semana, horas
Producto
1 2
1 1 0 4
2 0 2 12
3 3 2 18
Ganancia S/. 3000 S/. 5000

7. SOLUCIÓN
VARIABLES DE DECISIÓN:
X1: NÚMERO DE LOTES DEL PRODUCTO 1 FABRICADOS POR SEMANA.
X2: NÚMERO DE LOTES DEL PRODUCTO 2 FABRICADOS POR SEMANA.
MÁXIMIZAR 3X1+5X2
SUJETA A LAS RESTRICCIONES:
X1 ≤ 4
2X2 ≤ 12
3X1+2X2 ≤ 18
X1≥0 Y X2≥0

8. SOLUCIÓN ÓPTIMA
HACIENDO USO DE SOFTWARE O MÉTODO GRÁFICO: (PRUEBA DE OPTIMALIDAD)
X1= 2
X2= 6
VALOR ÓPTIMO: 3(2)+5(6)=36
EL EQUIPO DE INVESTIGACIÓN CONCLUYÓ QUE WYNDOR GLASS CO DEBE FABRICAR LOS PRODUCTOS 1 Y 2 A UNA TASA DE 2 Y 6
LOTES POR SEMANA, CON UNA GANANCIA SEMANAL TOTAL RESULTANTE DE 36 MIL SOLES SEMANALES.

9. EL PROBLEMA DE LA
WYNDOR GLASS CO.
SOLUCIÓN DE MODELOS DE PROGRAMACIÓN LINEAL CON DOS
VARIABLES MEDIANTE LA APLICACIÓN DE MÉTODO SIMPLEX

10. CONVERTIR RESTRICCIONES FUNCIONALES DE DESIGUALDAD
EN RESTRICCIONES DE IGUALDAD EQUIVALENTES
“INTRODUCIR VARIABLES DE HOLGURA O DE SUPERÁVIT”
ASUMAMOS:
EN LA PRIMERA RESTRICCIÓN X1 ≤ 4
LA VARIABLE DE HOLGURA DE ESTA RESTRICCIÓN SE DEFINE COMO:
X3: “HOLGURA O CANTIDAD NO USADA QUE QUEDA EN EL LADO IZQUIERDO DE LA
DESIGUALDAD”
EN CONSECUENCIA, LA RESTRICCIÓN ORIGINAL ES POR COMPLETO EQUIVALENTE A:
X1+X3=4 Y X3 ≥ 0

11. FORMA AUMENTADA DEL MODELO
MÁXIMIZAR Z= 3X1+5X2
SUJETA A LAS RESTRICCIONES:
Z- 3X1-5X2 = 0
X1 + X3 = 4
2X2 + X4 = 12
3X1+2X2 + X5 = 18
XJ≥0 PARA J=1,2,3,4,5.
Forma equivalente

12. MÉTODO SIMPLEX
Z- 3X1-5X2 = 0
X1 + X3 = 4
2X2 + X4 = 12
3X1+2X2 + X5 = 18
Forma tabular
Forma algebraica
Coeficiente
Variable
Básica Z X1 X2 X3 X4 X5
Lado
derecho
Z 1 -3 -5 0 0 0 0
X3 0 1 0 1 0 0 4
X4 0 0 2 0 1 0 12
X5 0 3 2 0 0 1 18
“Tabla simplex”

13. SOLUCIÓN ÓPTIMA
Planta
Tiempo de producción por
lote, horas
Tiempo de
producción
disponible a
la semana,
horas
Producto
1 2
1 1 0 4
2 0 2 12
3 3 2 18
Ganancia
por lote
S/. 3000 S/. 5000
Coeficiente
Variable
Básica Z X1 X2 X3 X4 X5
Lado
derech
o
Z 1 0 0 0 3/2 1 36
X3 0 0 0 1 1/3 -1/3 2
X2 0 0 1 0 ½ 0 6
X1 0 1 0 0 -1/3 1/3 2
X1=2 : Número de lotes del producto 1 a producir semanalmente
X2=6 : Número de lotes del producto 2 a producir semanalmente
X3=2 : ¿ ?

14. SOLUCIÓN ÓPTIMA
Planta
Tiempo de producción por lote,
horas
Tiempo de
producción
disponible a la
semana, horas
Producto
1 2
1 1 0 4
2 0 2 12
3 3 2 18
Ganancia
por lote
S/. 3000 S/. 5000
Coeficiente
Variable
Básica Z X1 X2 X3 X4 X5
Lado
derech
o
Z 1 0 0 0 3/2 1 36
X3 0 0 0 1 1/3 -1/3 2
X2 0 0 1 0 ½ 0 6
X1 0 1 0 0 -1/3 1/3 2
X1=2 : Número de lotes del producto 1 a producir semanalmente
X2=6 : Número de lotes del producto 2 a producir semanalmente
X3=2 : Número de horas disponibles en planta 1 al producir 2 lotes
del producto 1 de forma semanal.

15. EL PROBLEMA DE LA
WYNDOR GLASS CO.
TÉCNICA DE LA VARIABLE ARTIFICIAL

16. VARIABLES DE DECISIÓN:
X1: NÚMERO DE LOTES DEL PRODUCTO 1 FABRICADOS POR SEMANA.
X2: NÚMERO DE LOTES DEL PRODUCTO 2 FABRICADOS POR SEMANA.
MÁXIMIZAR 3X1+5X2
SUJETA A LAS RESTRICCIONES:
X1 ≤ 4
2X2 ≤ 12
3X1+2X2 = 18 “ASUMIENDO QUE LA PLANTA 3 USARÁ TODA SU CAPACIDAD”
X1≥0 Y X2≥0

17. FORMA AUMENTADA DEL MODELO
MÁXIMIZAR Z= 3X1+5X2
SUJETA A LAS RESTRICCIONES:
Z- 3X1-5X2 = 0
X1 + X3 = 4
2X2 + X4 = 12
3X1+2X2 = 18
XJ≥0 PARA J=1,2,3,4.
Aplicamos la técnica de la variable
artificial no negativa como si fuera una
variable de holgura.

18. FORMA AUMENTADA DEL MODELO
MÁXIMIZAR Z= 3X1+5X2
SUJETA A LAS RESTRICCIONES:
Z- 3X1-5X2 +MX5 = 0
X1 + X3 = 4
2X2 + X4 = 12
3X1+2X2 + X5 = 18
XJ≥0 PARA J=1,2,3,4. Aplicar método simplex
Restamos:
Z- 3X1-5X2 +Mx5 = 0
M(3X1+2X2 + x5 = 18)
___________________
Z-(3M+3) X1- (2M+5) X2=-
18M
Z=18M+(3M+3) X1+ (2M+5) X2

19. APLICACIÓN DEL MÉTODO SIMPLEX
Coeficiente
Variable
Básica Z X1 X2 X3 X4 X5
Lado derecho
Z 1 -3M-3 -2M-5 0 0 0 -18M
X3 0 1 0 1 0 0 4
X4 0 0 2 0 1 0 12
X5 0 3 2 0 0 1 18

20. SOLUCIÓN ÓPTIMA
Coeficiente
Variable
Básica Z X1 X2 X3 X4 X5
Lado
derecho
Z 1 0 0 0 3/2 M+1 36
X3 0 1 0 0 -1/3 1/3 2
X4 0 0 0 1 1/3 -1/3 2
X5 0 0 1 0 1/2 0 6