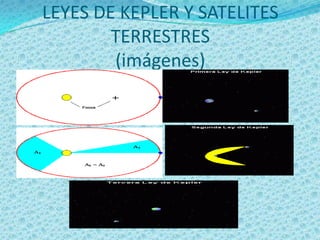
Este documento trata sobre conceptos relacionados con el movimiento circular y angular. Explica cómo se mide el ángulo y la velocidad angular, así como la aceleración centrípeta y angular. También describe la ley de la gravedad de Newton y las tres leyes de Kepler sobre los movimientos de los planetas.

2. INTRODUCCION
 Hay movimiento circular por todos lados, desde los
átomos hasta las galaxias, desde los flagelos de las
bacterias hasta las ruedas de la fortuna, solemos usar
dos términos para describir tales movimientos.

3. 7.1 MEDICIÓN ANGULAR
 Las ecuaciones de transformación
que relacionan un conjunto de
coordenadas con el otro son:
 Algo similar al desplazamiento lineal
es el desplazamiento angular, cuya
magnitud está dada por:
 °, o simplemente si elegimos ° 0°.
 Una unidad muy conveniente para
relacionar el ángulo con la longitud
del arco es el radián (rad). El ángulo
en radianes esta dado por la razón de
la longitud del arco (s) y el radio (r),
es decir, (en radianes) = cuando , el
ángulo es igual a un radián, rad, así,
escribimos (con el ángulo en
radianes).

4. MEDICION ANGULAR
(imágenes)


5. 7.2 RAPIDEZ Y VELOCIDAD
ANGULARES
 Usamos la letra griega minúscula
omega con una barra encima ( )
para representar la rapidez angular
promedio, que es la magnitud del
desplazamiento angular dividida
entre el tiempo total que tomo
recorrer esa distancia:
 Decimos que las unidades de la
rapidez angular son radianes por
segundo, como en el caso lineal, la
rapidez angular es constante,
entonces, = . Si tomamos ° y t°
como cero:
 O

6. RAPIDEZ Y VELOCIDAD ANGULARES
(imágenes)


7. 7.3 MOVIMIENTO CIRCULAR
UNIFORME Y ACELERACION
CENTRIPETA
 La aceleración centrípeta debe
dirigirse radialmente hacia
adentro, es decir, sin componente
en la dirección de la velocidad
Perpendicular (tangencial), pues si
no fuera así cambiaria la magnitud
de esa velocidad. Por lo tanto, es
como es a r, la fuerza centrípeta, al
igual que la aceleración
centrípeta, tiene dirección radial
hacia el centro de la trayectoria
circular.

8. MOVIMIENTO CIRCULAR UNIFORME Y ACELERACION
CENTRIPETA
(imágenes)

9. 7.4 ACELERACION ANGULAR
 Otro tipo de aceleración, es la aceleración
angular, esta cantidad representa la tasa de
cambio de la velocidad angular con respecto al
tiempo. Por similitud con el caso lineal, la
magnitud de la aceleración angular promedio ()
esta dada por: donde la barra sobre alfa indica
que es un valor promedio, como siempre.

10. ACELERACION ANGULAR
(imágenes)

11. 7.5 LEY DE LA GRAVITACION DE
NEWTON

12. LEY DE LA GRAVITACION DE
NEWTON

(imágenes)

13. 7.6 LEYES DE KEPLER Y SATELITES
TERRESTRES
 La fuerza de la gravedad determina los
movimientos de los planetas y satélites y
mantiene unido al sistema solar (y la galaxia).
 PRIMERA LEY DE KEPLER (ley de ORBITAS):
 “Los planetas se mueven en órbitas
elípticas, con el sol en uno de los puntos
focales.”.

 SEGUNDA LEY DE KEPLER (ley de áreas):
 “una línea del sol a un planeta barre áreas
iguales en lapsos de tiempo iguales”.

 TERCERA LEY DE KEPLER (ley de periodos):
 “el cuadrado del periodo orbital de un planeta
es directamente proporcional al cubo de la
distancia promedio entre el planta y el sol;”

14. LEYES DE KEPLER Y SATELITES
TERRESTRES
(imágenes)
