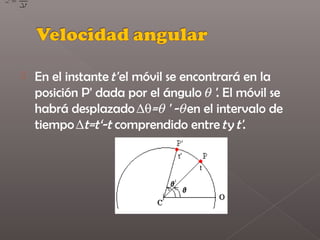
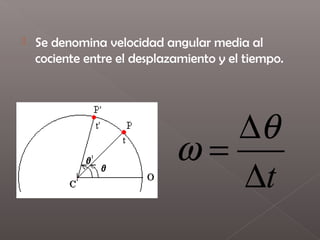
El documento define el movimiento circular y describe cómo se mide la posición angular, velocidad angular y aceleración angular de un objeto que se mueve en una trayectoria circular. Además, explica que la velocidad tangencial de un objeto en movimiento circular depende de su velocidad angular y que la aceleración total incluye tanto la aceleración centrípeta como la aceleración angular.

2. Se define movimiento circular como el movimiento de
un objeto cuya trayectoria dibuja una circunferencia.
Una vez situado el origen O de ángulos describimos el
movimiento circular mediante:
 Posición angular θ
 Velocidad angular ω
 Aceleración angular α

3.  En el instante t el móvil se encuentra en el punto
P. Su posición angular viene dada por el
ángulo q, que hace el punto P, el centro de la
circunferencia C y el origen de ángulos O.

4.  El ángulo θ, es el cociente entre la longitud del
arco s y el radio de la circunferencia r.
s
θ=
r

5.  En el instante t' el móvil se encontrará en la
posición P' dada por el ángulo θ '. El móvil se
habrá desplazado ∆θ=θ ' -θ en el intervalo de
tiempo ∆t=t‘-t comprendido entre t y t'.

6.  Se denomina velocidad angular media al
cociente entre el desplazamiento y el tiempo.
∆θ
ω=
∆t

7. Si en el instante t la velocidad angular del móvil
es ω y en el instante t' la velocidad angular del
móvil es ω'. La velocidad angular del móvil ha
cambiado ∆ω=ω' -ω en el intervalo de
tiempo ∆t=t'-t comprendido entre t y t'.

8. Se denomina aceleración angular media al
cociente entre el cambio de velocidad angular y
el intervalo de tiempo que tarda en efectuar
dicho cambio.
∆ω
α=
∆t

9. Es una distancia recorrida por una partícula en una
trayectoria circular y se expresa frecuentemente en radianes
(rad), grados (°) y revoluciones (rev); es conveniente
expresar toda rotación en radianes. El radian es una
unidad de medida angular, así como el metro es la unidad
de medida lineal.
Se define al radián como el ángulo subtendido por el arco
del círculo cuya longitud es igual al radio del mismo círculo.
Como el perímetro de un círculo es 2 π por el radio r, hay 2
π radian en un circulo completo.
1rev = 2 π radian = 360°

10. Como el movimiento lineal, el movimiento circular puede
ser uniforme o acelerado. La rapidez de rotación varía
bajo la influencia de un momento de torsión resultante.
La aceleración angular se define como la variación de la
velocidad angular con respecto al tiempo y esta dada por:
∝ = ωf - ωi
t
∝ = velocidad angular final en rad/ s2
ωf = velocidad angular final en rad/s
ωi = velocidad angular inicial en rad/s
t = tiempo transcurrido en seg.

11. Este movimiento ocurre sobre una circunferencia, pero se
diferencia del anterior en que la velocidad tangencial
aumenta uniformemente a medida que la partícula recorre
la circunferencia.
A medida que pasa el tiempo, la velocidad tangencial
aumenta, esto es debido a que la velocidad angular w
aumenta uniformemente a medida que se recorre la
circunferencia, este cambio genera una aceleración
angular g definida a continuación. La aceleración total es la
suma vectorial de la aceleración centrípeta y la aceleración
angular.

12. Como se ve en la figura, a medida que pasa el tiempo, la velocidad tangencial aumenta,
esto es debido a que la velocidad angular w aumenta uniformemente a medida que se
recorre la circunferencia, este cambio genera una aceleración angular g definida a
continuación. La aceleración total es la suma vectorial de la aceleración centrípeta y la
aceleración angular.

13. Una rueda de bicicleta de 30 cm de radio comienza a girar
desde el reposo con una aceleración angular constante de 3
rad/s2. Después de 10 segundos calcular:
a)Su rapidez angular b) El desplazamiento angular

14. c) La rapidez tangencial de un punto del borde
R: a) Rapidez Angular: 30 rad/s
b) Desplazamiento angular: 150 rad
c) Rapidez Tangencial: 9 m/s