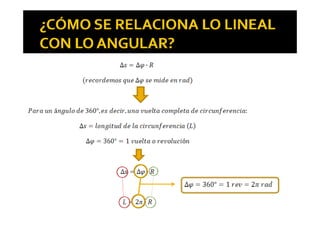
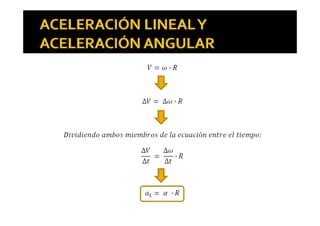
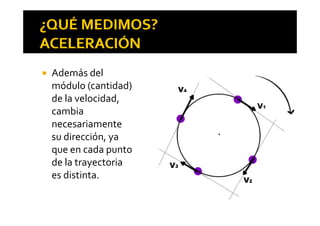
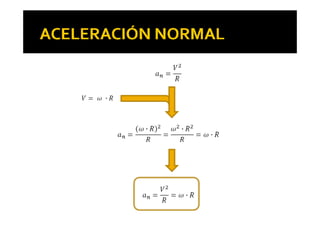
El documento trata sobre el movimiento circular, donde se analizan las trayectorias circunferenciales y las magnitudes asociadas como la velocidad lineal y la velocidad angular. Se explica la relación entre estas magnitudes a través del radián y cómo se relacionan con las unidades de medida. Además, se menciona la existencia de aceleraciones lineales y angulares, así como la aceleración normal que actúa hacia el centro de giro.

2. “Es aquél en que un móvil describe una
trayectoria circunferencial alrededor del trayectoria circunferencial alrededor del
centro de dicha circunferencia, que
d i d idenominamos centro de giro.”

3. En el movimiento rectilíneo medimos posiciones yEn el movimiento rectilíneo, medimos posiciones y
tiempo.
En el movimiento circular además de la trayectoriaEn el movimiento circular, además de la trayectoria
(espacio), medimos el giro que realiza el móvil
(ángulo)(ángulo).

5. Según cambia el espacio o el ángulo a lo largo
del tiempo tenemos dos velocidadesdel tiempo, tenemos dos velocidades:
Velocidad lineal (V): espacio recorrido por unidad
de tiempo
Vel0cidad angular (ω): ángulo recorrido porVel0cidad angular (ω): ángulo recorrido por
unidad de tiempo

6. El espacio recorrido depende tanto del
ángulo recorrido como del radio de laángulo recorrido como del radio de la
circunferencia:
A mayor ángulo, mayor espacio.y g , y p
A mayor radio mayor espacioA mayor radio, mayor espacio.

7. La relación entre las magnitudes lineales y las
l l é d d d dangulares se realiza a través de una unidad de
medida de ángulos: el radián.g

8. “Un radián se define como un ángulo cuyo
id l i diarco mide lo mismo que su radio.”

11. A partir de la definición de radián, podemos
l l d l lrelacionar las magnitudes angulares con las
lineales.

13. li l i l l l l i li d“Lo lineal es igual a lo angular multiplicado
por el radio.”p

14. Ya que las velocidades son los cambios del
espacio (velocidad lineal) o del ánguloespacio (velocidad lineal) o del ángulo
(velocidad angular) en el tiempo, de la
ó d b lexpresión anterior podemos obtener la
relación entre velocidad angular y velocidadg y
lineal.

16. A través de la relación entre ángulo y espacioA través de la relación entre ángulo y espacio
también podemos deducir la fórmula de la
l d d l f í llongitud de la circunferencia, así como la
relación entre las distintas unidades de
medida de los ángulos.

18. En el movimiento circular también puede
existir la aceleración es decir un cambio en laexistir la aceleración, es decir, un cambio en la
velocidad. Puede ser:
Aceleración lineal (at): cambio en el módulo de la( t)
velocidad lineal
Aceleración angular (α): cambio en el módulo de
la velocidad angularla velocidad angular

19. Al igual que con el resto de magnitudes, las
l l l l áaceleraciones lineal y angular están
relacionadas a través del radio.

21. Además del
módulo (cantidad) módulo (cantidad)
de la velocidad,
cambia cambia
necesariamente
su dirección ya su dirección, ya
que en cada punto
de la trayectoria de la trayectoria
es distinta.

22. Esta variación en la dirección de la velocidad
b é l ó l l iótambién es una aceleración: la aceleración
normal (an)n

23. El vector de la
aceleración aceleración
normal es
d l lperpendicular al
de la lineal o
tangencial, y se
dirige siempre dirige siempre
hacia el centro de
girogiro.

25. UNIDAD EN EL S.I.
OTRAS UNIDADES DE USO
COMÚN
CONVERSIÓN DE
UNIDADES
Kilómetro (Km)
Centímetro (cm)
Espacio (s) Metro (m)
Centímetro (cm)
…
Pulgada (‘)
Milla (mi)
(Sistema anglosajón o imperial)
1 m=100 cm =0.001 km
Ángulo ( ) Radián (rad)
Grado sexagesimal (°)
Vuelta o revolución (rev)
Grado centesimal (g)
2π rad = 360° = 1 rev = 400g
Kilómetros por hora (km/h)
Mediante factores de
Velocidad lineal (V) Metros por segundo (m/s) …
Millas por hora (mi/h)
Mediante factores de
conversión
Velocidad angular (ω) Radianes por segundo (rad/s) ‐
Mediante factores de
conversión
Aceleración lineal o
tangencial (at)
Metros por segundo al
cuadrado (m/s2) ‐
Mediante factores de
conversión
Aceleración angular
Radianes por segundo al
cuadrado (rad/s2) ‐
Mediante factores de
conversión
Aceleración normal (an)
Metros por segundo al
cuadrado (m/s2) ‐
Mediante factores de
conversión

26. “Es aquél en que un móvil describe una trayectoria circunferencial
alrededor del centro de dicha circunferencia, que denominamos centro
d i ”de giro.”
El radián es un ángulo cuyo arco tiene la misma longitud que su radio.
22ππ rad = 360rad = 360°° = 1 vuelta o revolución= 1 vuelta o revolución

27. Medimos:
Espacio (s) Velocidad lineal
(V)
Aceleración
lineal (at)
Aceleración
normal (an)
Ángulo ( ) Velocidad
angular (ω)
Aceleración
angular (α)