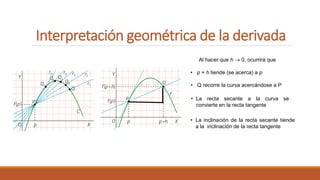
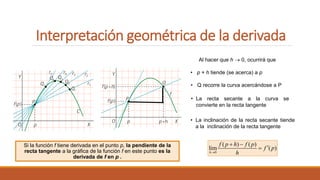
El documento presenta conceptos sobre la interpretación geométrica de la derivada. Explica que al hacer que h se acerque a 0, la recta secante se convierte en la recta tangente. También presenta la ecuación de la recta tangente y normal, y resuelve ejercicios aplicando estos conceptos.

1. Matemáticas II
SEMANA 1 (PERIODO INTENSIVO)
PROF. KEIBER CAMACARO

2. Interpretación geométrica de la derivada
Al hacer que h  0, ocurrirá que
• p + h tiende (se acerca) a p
• Q recorre la curva acercándose a P
• La recta secante a la curva se
convierte en la recta tangente
• La inclinación de la recta secante tiende
a la inclinación de la recta tangente

3. Interpretación geométrica de la derivada
Al hacer que h  0, ocurrirá que
• p + h tiende (se acerca) a p
• Q recorre la curva acercándose a P
• La recta secante a la curva se
convierte en la recta tangente
• La inclinación de la recta secante tiende
a la inclinación de la recta tangente
Si la función f tiene derivada en el punto p, la pendiente de la
recta tangente a la gráfica de la función f en este punto es la
derivada de f en p .
0
( ) ( )
lim ( )
h
f p h f p
f p
h

 



4. Ecuación de la recta tangente
a
f(a)
at
at
Entonces:
• Pendiente de la tangente: 𝒎𝒕 = 𝒇 ′(𝒂)
• Ecuación de la recta tangente:
𝒕 ∶ 𝒚 – 𝒇(𝒂) = 𝒇 ′(𝒂) (𝒙 – 𝒂)
t
Ecuación de la recta que pasa por un
punto 𝐴(𝑎, 𝑏) y de pendiente 𝑚:
𝑦 – 𝑏 = 𝑚 (𝑥 – 𝑎)

5. Ecuación de la recta normal
Como la tangente y la normal son
perpendiculares sus pendientes son
inversas y cambiadas de signo.
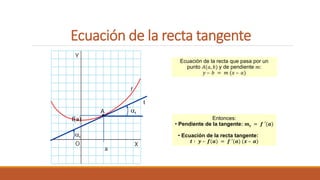
Entonces:
Pendiente de la tangente: 𝑚𝑡 = 𝑓 ′(𝑝)
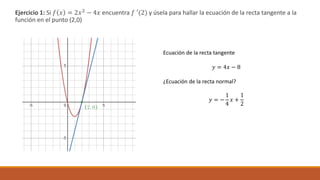
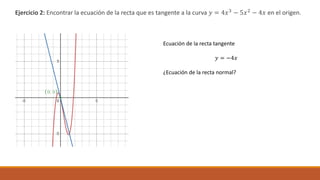
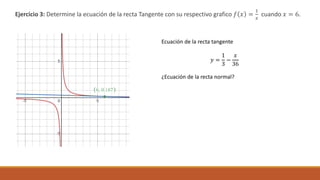
Ecuación de la recta tangente:
𝑦 – 𝑓(𝑝) = 𝑓 ′(𝑝) (𝑥 – 𝑎)
Pendiente de la normal:
𝑚𝑛 = – 1/𝑓′(𝑝)
Ecuación de la normal:
𝑦 – 𝑓(𝑝) = [– 1/𝑓 ′(𝑝)] (𝑥 – 𝑎)
Ecuación de una recta que pasa por un punto
𝑃(𝑝, 𝑓(𝑝)) y de pendiente 𝑚:
𝑦 – 𝑓(𝑝) = 𝑚 (𝑥 – 𝑝)

6. Ejercicio 1: Si 𝑓 𝑥 = 2𝑥2 − 4𝑥 encuentra 𝑓 ′(2) y úsela para hallar la ecuación de la recta tangente a la
función en el punto (2,0)

7. Ejercicio 1: Si 𝑓 𝑥 = 2𝑥2 − 4𝑥 encuentra 𝑓 ′(2) y úsela para hallar la ecuación de la recta tangente a la
función en el punto (2,0)
Ecuación de la recta tangente
𝑦 = 4𝑥 − 8
¿Ecuación de la recta normal?
𝑦 = −
1
4
𝑥 +
1
2

8. Ejercicio 2: Encontrar la ecuación de la recta que es tangente a la curva 𝑦 = 4𝑥3 − 5𝑥2 − 4𝑥 en el origen.

9. Ejercicio 2: Encontrar la ecuación de la recta que es tangente a la curva 𝑦 = 4𝑥3 − 5𝑥2 − 4𝑥 en el origen.
Ecuación de la recta tangente
𝑦 = −4𝑥
¿Ecuación de la recta normal?

10. Ejercicio 3: Determine la ecuación de la recta Tangente con su respectivo grafico 𝑓 𝑥 =
1
𝑥
cuando 𝑥 = 6.
¿Cómo es la gráfica de 𝒇 𝒙 ?

11. Ejercicio 3: Determine la ecuación de la recta Tangente con su respectivo grafico 𝑓 𝑥 =
1
𝑥
cuando 𝑥 = 6.

12. Ejercicio 3: Determine la ecuación de la recta Tangente con su respectivo grafico 𝑓 𝑥 =
1
𝑥
cuando 𝑥 = 6.
Ecuación de la recta tangente
𝑦 =
1
3
−
𝑥
36
¿Ecuación de la recta normal?

13. Ejercicio 4: Encuentre todos los puntos en la gráfica de 𝑦 =
1
3
𝑥3 + 𝑥2 − 𝑥, en donde la recta tenga
pendiente 1.

14. Recuerda,
𝑓′
𝑥 =
𝑑
𝑑𝑥
𝑓 𝑥
𝑦′ =
𝑑𝑦
𝑑𝑥
=
𝑑
𝑑𝑥
𝑦
En los libros encontrarás
notaciones diferentes que
representan lo mismo,
aprende a familiarizarte de
ellas

15. Reglas básicas de derivación
¿Cuál es la derivada de la función 𝑦 = 𝑥3 + 2𝑥2 − 4𝑥 + 5 ?

16. Reglas básicas de derivación
¿Cuál es la derivada de la función 𝑦 = 𝑥3 + 2𝑥2 − 4𝑥 + 5 ?
Solución: ¿Qué debemos considerar sobre la función?
Dada 𝑦 = 𝑥3 + 2𝑥2 − 4𝑥 + 5

17. Reglas básicas de derivación
Deriva la función 𝑦 =
3
𝑥2

18. Reglas básicas de derivación
Deriva la función 𝑦 =
3
𝑥2
Solución: ¿Cómo podemos simplificar el cálculo de la derivada?
Dada 𝑦 =
3
𝑥2 = 𝑥2/3

19. Reglas básicas de derivación
Determina la derivada de la función 𝑦 = 23
𝑥 −
7
𝑥

20. Reglas básicas de derivación
Determina la derivada de la función 𝑦 = 23
𝑥 −
7
𝑥
Solución:
Dada la función 𝑦 = 23
𝑥 −
7
𝑥

21. Reglas básicas de derivación
Determina la derivada de la función 𝑦 = 𝑥 𝑥 + 1

22. Reglas básicas de derivación
Determina la derivada de la función 𝑦 = 𝑥 𝑥 + 1
Solución: Considera que se trata del producto de dos funciones.
Dada la función 𝑦 = 𝑥 𝑥 + 1

23. Reglas básicas de derivación
Determina la derivada de la función 𝑦 =
𝑥2−5
1−3𝑥2

24. Reglas básicas de derivación
Determina la derivada de la función 𝑦 =
𝑥2−5
1−3𝑥2
Solución: Considera que se trata del cociente de dos funciones.
Dada la función 𝑦 =
𝑥2−5
1−3𝑥2