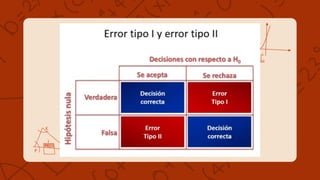
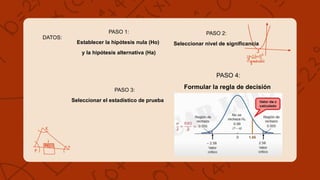
La prueba de hipótesis es un procedimiento para verificar suposiciones acerca de parámetros poblacionales, siendo la hipótesis nula la que se prueba y la alternativa la que se acepta si se rechaza la nula. Se presentan ejemplos prácticos sobre la vida útil de bombillos y la producción de escritorios, donde se demuestra cómo determinar si la media de muestras es diferente a un valor específico. Además, se discuten los errores tipo 1 y tipo 2 que pueden ocurrir durante la prueba y sus implicaciones en decisiones empresariales.

1. Prueba de
Hipótesis
Equipo 1: Estadística inferencial 1

2. Qué es la
hipótesis?
Afirmación relativa a un
parámetro de la población
subjetiva a verificación.
En estadística, una hipótesis es
una aseveración o afirmación
acerca de una propiedad de
una población
Qué es la prueba
de hipótesis?
Es un procedimiento estándar
para probar una aseveración
acerca de una propiedad de
una población
Comienza con una afirmación o
suposición sobre un
parámetro de la población
como podría ser la media
poblacional.

3. Qué es la hipótesis
nula?
Es cualquier hipótesis
que se desea
probar.
Se denota por
Qué es la hipótesis
alternativa?
Es la hipótesis que se
acepta cuando la
hipótesis nula es
rechazada.

4. Ejemplo 1
Una empresa produce bombillos, se espera que éstos
tengan una vida de 1000 horas cuando se venden, eso es lo
que se ofrece a los compradores.
La gerencia tiene dudas ya que hay clientes que se quejan
de que los bombillos no alcanzan las 1000 horas. Se toma
una muestra bombillos al azar.
En esta situación se debe determinar si la afirmación
La vida de los bombillos es 1,000 horas es verdadera o falsa

5. Esta afirmación cuya veracidad se prueba se conoce como
hipótesis. El procedimiento para realizar esta evaluación se
llama prueba de hipótesis.
Entonces si se rechaza la hipótesis nula de que la vida media
de los bombillos es 1000 horas, se estaría tomando por valida
la hipótesis alternativa:
La vida media de los bombillos es menor que 1000 horas

6. Suponga que la empresa tomó una muestra de 24
bombillos y los probó para determinar la vida media. Y así
contar con datos para la prueba de hipótesis
¿se puede concluir que la vida media de los bombillos es
menor que 1000 horas?
Un principio es que si la hipótesis nula se rechaza solo si los
datos ofrecen suficiente evidencia para no considerarla
verdadera. Explicación…

7. ¿ como se sabe qué tanto es suficiente evidencia?
Nivel de confianza: es la probabilidad de rechazar la
hipótesis nula cuando es verdadera. Se denota por

9. ¿Como ingenieros, qué significan estos errores para
la empresa?
Error del tipo 1: Los bombillos de la muestra tenían
una vida muy baja y se rechaza que la vida media es
de 1000 horas siendo verdadera esta hipótesis.
Consecuencia: La empresa va a tratar de mejorar
su proceso de producción innecesariamente, lo
cual le hará incurrir en costos mayores

10. ¿Como ingenieros, qué significan estos errores para
la empresa?
Error del tipo 2: Los bombillos de la muestra tenían
una vida muy alta y se acepta que la vida media es de
1000 horas siendo falsa esta hipótesis.
Consecuencia: La empresa no va a tratar de
mejorar su proceso de producción pero debería
de hacerlo, lo cual le va a generar clientes
insatisfechos.

11. Una empresa fabrica y arma escritorios y otros muebles para oficina.
La producción semanal del escritorio modelo A325 tiene una
distribución normal, con una media de 200 y una desviación estándar
de 16. Hace poco, con motivo de la expansión del mercado, se
introdujeron nuevos métodos de producción y se contrató a más
empleados. El vicepresidente de fabricación pretende investigar si
hubo algún cambio en la producción semanal del escritorio. En otras
palabras, ¿La cantidad media de escritorios que se produjeron es
diferente de 200 escritorios semanales?, utilice un nivel de significancia
de 0.01. En una muestra de 50 semanas la cantidad media de
escritorios que se produjeron fue de 203.5.

12. DATOS:
PASO 1:
Establecer la hipótesis nula (Ho)
y la hipótesis alternativa (Ha)
PASO 2:
Seleccionar nivel de significancia
PASO 3:
Seleccionar el estadístico de prueba
PASO 4:
Formular la regla de decisión

13. PASO 5:
Se toma una decisión y se interpretan los
resultados
- NO se rechaza la Ho:
La no es distinta de
¿La cantidad media de escritorios que se produjeron
es diferente de 200 escritorios semanales? NO

14. Tema 2: Confiabilidad y significancia
 Denominada también prueba de significación, tiene como
objetivo principal evaluar suposiciones o afirmaciones acerca
de los valores estadísticos de la población, denominadas
parámetros.
 La confiabilidad de un instrumento se refiere a la constitución
interna de las personas, a la mayor o menor acescencia de
errores de medida. Un instrumento confiable significa que si
lo aplicamos por más de una vez a un mismo elemento
entonces obtendríamos resultados iguales.

15.  Confiabilidad se refiere al grado en que la aplicación repetida del
instrumento ( a las mismas unidades de estudio en idénticas
condiciones) produce iguales resultados. Implica precisión en la
medición. Cuanto mayor es la diferencia entre medidas de las mismas
características, realizadas en diferentes momentos, menor es la
confiabilidad del instrumento.
 Todos los métodos utilizan formulas que producen coeficientes de
confiabilidad estos coeficientes pueden oscilar entre 0 y , donde un
coeficiente de 0 significa nulo confiabilidad y 1 representa el máximo de
confiabilidad

16. Tema 3

17. Ejemplo 1: Identificación de errores del tipo 1 y tipo 2
Una gran encuesta a nivel nacional realizada recientemente mostró una tasa
de desempleo del 9% en EE.UU.
La alcaldesa de cierta ciudad desea averiguar si estos resultados son válidos
para su ciudad, por lo que decide tomar una muestra entre los residentes para
verificar si la tasa de desempleo en su ciudad es significativamente diferente al
9%.
Sea p la tasa de desempleo en su ciudad. Las siguientes son las hipótesis que
establecerá:
¿Bajo cuál de las siguientes condiciones la alcaldesa estaría incurriendo en un
error del tipo 1?

18. A) Ella concluye que la tasa de desempleo en la ciudad no es del 9% cuando en
realidad sí es.
B) Ella concluye que la tasa de desempleo en la ciudad no es del 9%, cuando en
realidad no es.
C) Ella concluye que la tasa de desempleo en la cuidad es del 9%, cuando en realidad sí
es.
D) Ella concluye que la tasade desempleo en la cuidad es del 9%, cuando en realidad
no es.

19. Ejemplo 2: Análisis de errores del tipo 1 y tipo 2
En el tecnológico desean abrir otra cafetería. Para ello se decide realizar una encuentra a una
muestra de estudiantes, con el objetivo de verificar si hay evidencia contundente de que la
proporción de estudiantes interesados en consumir en la cafetería es mayor que el 40%; en
dado caso, se considerará construir una nueva cafetería.
Sea p la proporción de estudiantes interesados en consumir en la cafetería.
Estas son las hipótesis planteadas:
¿Cuáles son las implicaciones de un tipo 2 en este caso?
a) No se considera construir una nueva cafetería a pesar de que se requiere.
b) No se considera construir una nueva cafetería pues no se requiere
c) Se considera construir una nueva cafetería a pesar de que no se requiere.
d) Se considera construir una cafetería pues así se requiere.

20. Tema 5: Proceso para hacer una prueba de hipótesis
• Se establece la hipótesis nula y la hipótesis alternativa.
• se selecciona un nivel de significancia para la prueba.
• Se identifica el estadístico de prueba (depende del tipo de prueba)
• Se formula una regla para tomar decisiones
• Se toma una muestra y se llega a una decisión; aceptar o rechazar la
hipótesis nula.

21. Ejemplo 1:
Un cierto material viene en cajas de peso promedio 17 libras y desviación
estándar 0.4 libras.
Se recibe un cargamento grande y se tiene una sospecha de que el peso
promedio de las caja es inferior al usual.
Para verificar la sospecha se toma una muestra al azar de 86 cajas y se pesan,
obteniendo un promedio de 16.5 libras.
¿se puede afirmar que efectivamente el peso de las cajas es inferior al
acostumbrado?
Use un nivel de significancia del 5%

22. Datos:
población
Muestra:
N=86
Significancia
1. Plantear la hipótesis:
2. Nivel de significancia:
3. Estadístico de prueba:
n=86 (n
Prueba de una cola (porque : )
( una cola) entonces
4. Regla de decisión: (en valor absoluto)
, se rechaza
5. Se tiene suficiente evidencia estadística para rechazar la
hipótesis nula con un nivel de significancia del 5%