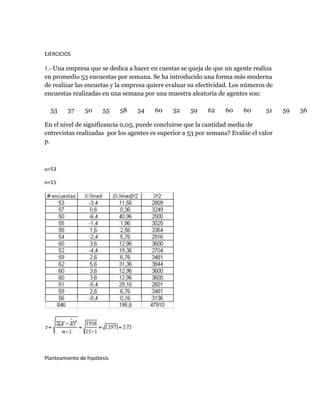
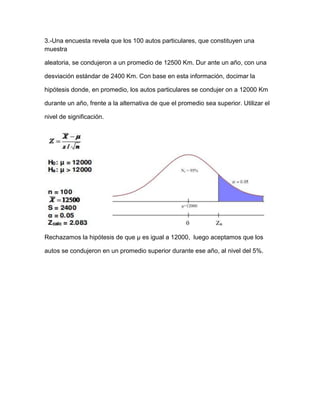
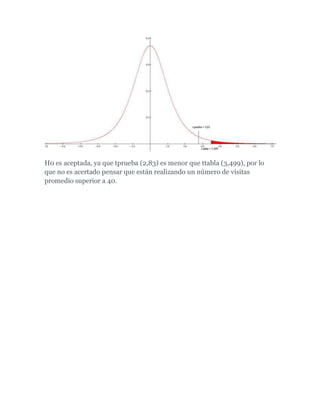
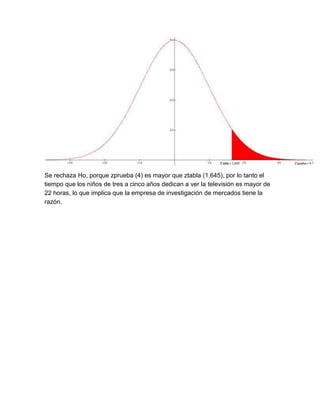
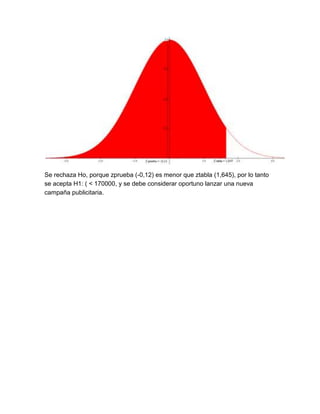
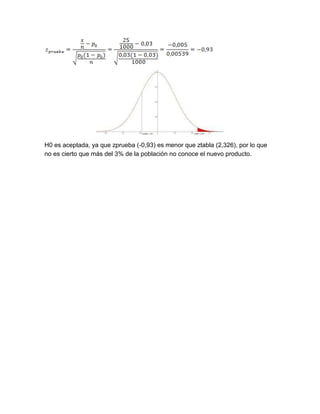
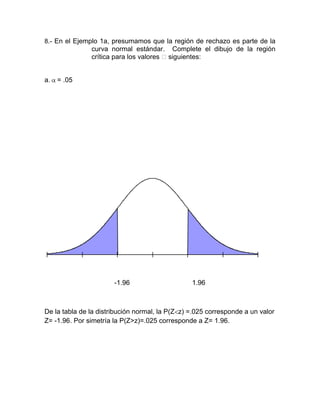
Este documento presenta una explicación sobre pruebas de hipótesis. Define las hipótesis nula (Ho) y alternativa (H1), indicando que Ho se refiere a un valor específico del parámetro poblacional mientras que H1 difiere de Ho. Explica el proceso de contrastar las hipótesis y tomar una decisión sobre rechazar o no Ho a favor de H1. Luego, presenta algunos ejercicios de aplicación de pruebas de hipótesis con sus respectivas soluciones.

1. UNIVERSIDAD TECNOLOGICA DE TORREÓN
CARRERA: PROCESOS INDUSTRIALES EN EL ÁREA DE
MANUFACTURA
NOMBRE:KAREM LUCERO GARCIA VITELA
GRADO Y SECCIÓN: 2°B

2. PRUEBA DE HIPÓTESIS
Una prueba de hipótesis consiste en contrastar dos hipótesis estadísticas. Tal contraste involucra
la toma de decisión acerca de las hipótesis. La decisión consiste en rechazar o no una hipótesis en
favor de la otra. Una hipótesis estadística se denota por “H” y son dos:
- Ho: hipótesis nula
- H1: hipótesis alternativa
Hipótesis nula “Ho”
Se refiere siempre a un valor especifico del parámetro de la población, no a una estadística de
muestra. La letra H significa hipótesis y el subíndice cero no hay diferencia. Por lo general hay un
“no” en la hipótesis nula que indica que “no hay cambio” Podemos rechazar o aceptar Ho.
Por lo tanto la hipótesis nula es una afirmación que no se rechaza a menos que los datos
muestrales proporcionen evidencia convincente de que es falsa. El planteamiento de la hipótesis
nula siempre contiene un signo de igualdad con respecto al valor especificado del parámetro.
Hipótesis alternativa “H1”
Es cualquier hipótesis que difiera de la hipótesis nula. Es una afirmación que se acepta si los datos
muestrales proporcionan evidencia suficiente de que la hipótesis nula es falsa. Se le conoce
también como la hipótesis de investigación. El planteamiento de la hipótesis alternativa nunca
contiene un signo de igualdad con respecto al valor especificado del parámetro.

3. EJERCICIOS
1.- Una empresa que se dedica a hacer en cuestas se queja de que un agente realiza
en promedio 53 encuestas por semana. Se ha introducido una forma más moderna
de realizar las encuetas y la empresa quiere evaluar su efectividad. Los números de
encuestas realizadas en una semana por una muestra aleatoria de agentes son:
53 57 50 55 58 54 60 52 59 62 60 60 51 59 56
En el nivel de significancia 0,05, puede concluirse que la cantidad media de
entrevistas realizadas por los agentes es superior a 53 por semana? Evalúe el valor
p.
u=53
n=15
Planteamiento de hipótesis

4. a) Prueba de una cola
b) Nivel de significancia 0,05
c) Estadístico de prueba
Xmed =846/5= 56,4
d)Planear la regla de decisión.
Alfa= 0,05
Gl= n -1 = 15 – 1 =14
Si t es < 1,761 se rechaza Ho y se acepta H1
Tomar decisión:
Como t (3,53) > 1,761 se rechaza la hipótesis nula y se acepta H1 y se concluye que la cantidad
media de entrevistas realizadas por los agentes es mayor a 53 por semana.
Valor p= 1,761 es 0,4989
P= 0,50 – 0,4989 = 0,0011

5. 2.- Un criador de pollos sabe por experiencia que el peso de los pollos de cinco
meses es 4,35 libras. Los pesos siguen una distribución normal. Para tratar de
aumentar el peso de dichas aves se le agrega un aditivo al alimento. En una
muestra de pollos de cinco meses se obtuvieron los siguientes pesos ( en libras).
4,41 4,37 4,33 4,35 4,30 4,39 4,36 4,38 4,40 4,39
En el nivel 0,01, el aditivoa ha aumentado el peso medio de los pollos? Estime el
valor de p
N=10
U=4,36
Xmed= 4,368
Xmed= 43,68/10 = 4,368
Planteamiento de hipótesis
a) Prueba de una cola
b) Nivel de significancia 0,01

6. c) Estadístico de prueba
área = 0,4535
D)plantear la regla de decisión:
Alfa= 0,01
Gl=n-1= 10-1= 9
Si t> 2,821 Se rechazo Ho y se acepta H1
Tomar decisión:
Como t(1,68) < 2,821 se acepta la hipótesis nula y se rechaza H1 y se concluye que el aditivo no
aumenta el peso medio de los pollos en un 4,35
Valor p= 1,68 es 0,4535
P=0,05 – 0,4535 = 0,046

7. 3.-Una encuesta revela que los 100 autos particulares, que constituyen una
muestra
aleatoria, se condujeron a un promedio de 12500 Km. Dur ante un año, con una
desviación estándar de 2400 Km. Con base en esta información, docimar la
hipótesis donde, en promedio, los autos particulares se condujer on a 12000 Km
durante un año, frente a la alternativa de que el promedio sea superior. Utilizar el
nivel de significación.
Rechazamos la hipótesis de que µ es igual a 12000, luego aceptamos que los
autos se condujeron en un promedio superior durante ese año, al nivel del 5%.

8. 4.- Un gerente de ventas de libros universitarios afirma que en promedio sus
representantes de ventas realiza 40 visitas a profesores por semana. Varios de
estos representantes piensan que realizan un número de visitas promedio superior
a 40. Una muestra tomada al azar durante 8 semanas reveló un promedio de 42
visitas semanales y una desviación estándar de 2 visitas. Utilice un nivel de
confianza del 99% para aclarar esta cuestión.
( = 40
n=8
Nivel de confianza del 99%
Nivel de significación = (100%-99%)/2 = 0,5% = 0,005
Solución:
H0: ( = 40
H1: ( > 40
Grados de libertad: n-1 = 8-1 =7
a = 0,005

9. H0 es aceptada, ya que tprueba (2,83) es menor que ttabla (3,499), por lo
que no es acertado pensar que están realizando un número de visitas
promedio superior a 40.

10. 5.- Un investigador de mercados y hábitos de comportamiento afirma que
el tiempo que los niños de tres a cinco años dedican a ver la televisión cada
semana se distribuye normalmente con una media de 22 horas y desviación
estándar 6 horas. Frente a este estudio, una empresa de investigación de
mercados cree que la media es mayor y para probar su hipótesis toma una
muestra de 64 observaciones procedentes de la misma población, obteniendo
como resultado una media de 25. Si se utiliza un nivel de significación del 5%.
Verifique si la afirmación del investigador es realmente cierta
Datos:
n = 64
a = 5% = 0,05
Solución:
H0: ( = 22
H1: ( > 22
a = 0,05

11. Se rechaza Ho, porque zprueba (4) es mayor que ztabla (1,645), por lo tanto el
tiempo que los niños de tres a cinco años dedican a ver la televisión es mayor de
22 horas, lo que implica que la empresa de investigación de mercados tiene la
razón.

12. 6.- Cuando las ventas medias, por establecimiento autorizado, de una marca de
relojes caen por debajo de las 170,000 unidades mensuales, se considera razón
suficiente para lanzar una campaña publicitaria que active las ventas de esta
marca. Para conocer la evolución de las ventas, el departamento
demarketing realiza una encuesta a 51 establecimientos autorizados,
seleccionados aleatoriamente, que facilitan la cifra de ventas del último mes en
relojes de esta marca. A partir de estas cifras se obtienen los siguientes
resultados: media = 169.411,8 unidades., desviación estándar = 32.827,5
unidades. Suponiendo que las ventas mensuales por establecimiento se
distribuyen normalmente; con un nivel de significación del 5 % y en vista a la
situación reflejada en los datos. ¿Se considerará oportuno lanzar una nueva
campaña publicitaria?
Datos:
n = 51
Solución:
H0: ( = 170000
H1: ( < 170000
a = 0,05

13. Se rechaza Ho, porque zprueba (-0,12) es menor que ztabla (1,645), por lo tanto
se acepta H1: ( < 170000, y se debe considerar oportuno lanzar una nueva
campaña publicitaria.

14. 7.- Una empresa está interesada en lanzar un nuevo producto al mercado. Tras
realizar una campaña publicitaria, se toma la muestra de 1 000 habitantes, de los
cuales, 25 no conocían el producto. A un nivel de significación del 1% ¿apoya el
estudio las siguientes hipótesis?
a. Más del 3% de la población no conoce el nuevo producto.
b. Menos del 2% de la población no conoce el nuevo producto
Datos:
n = 1000
x = 25
Donde:
x = ocurrencias
n = observaciones
= proporción de la muestra
= proporción propuesta
Solución:
a)
a = 0,01

15. H0 es aceptada, ya que zprueba (-0,93) es menor que ztabla (2,326), por lo que
no es cierto que más del 3% de la población no conoce el nuevo producto.

16. 8.- En el Ejemplo 1a, presumamos que la región de rechazo es parte de la
curva normal estándar. Complete el dibujo de la región
crítica para los valores siguientes:
a. = .05
-1.96 1.96
De la tabla de la distribución normal, la P(Z z) =.025 corresponde a un valor
Z= -1.96. Por simetría la P(Z>z)=.025 corresponde a Z= 1.96.