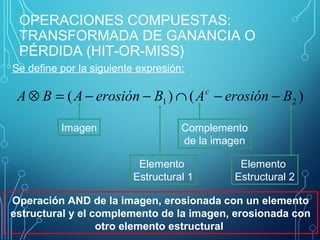
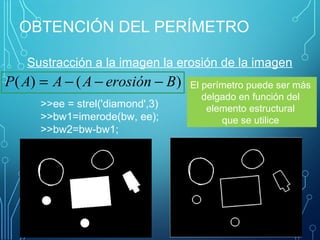
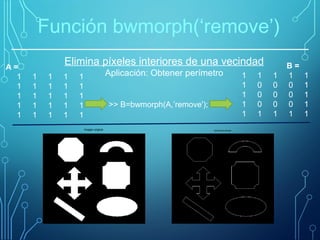
Este documento describe operaciones morfológicas en MATLAB. Explica conceptos como dilatación, erosión, elementos estructurales y transformada de distancia. La dilatación agrega píxeles al contorno de objetos, mientras que la erosión elimina píxeles. Estas operaciones se utilizan comúnmente para procesamiento de imágenes como limpieza, detección de bordes y medición de propiedades.

1. OPERACIONES
MORFOLÓGICAS EN
MATLAB

2. MORFOLOGÍA
• Morfología: Rama de la biología que trata de la
forma y estructura de animales y plantas.
• Morfología Aplicada a las Imágenes: Herramientas
y métodos utilizados para extraer componentes de
la misma, útiles de la descripción y representación
de formas.

3. OPERACIONES MORFOLÓGICAS
El valor de cada píxel en la imagen de salida
depende del valor de ese píxel en la imagen de
entrada y su relación con la vecindad
1 0 0
0 0 0
0 0 0
1 1 1
1 1 1
1 1 1

4. ELEMENTO ESTRUCTURAL
Elemento estructural: Define la forma y el tamaño de la
vecindad del píxel que será analizado, para posteriormente
alterar su valor
Composición: Formada por ceros y unos de forma y tamaño
arbitrario en la cual las posiciones donde está el uno
define la vecindad
Matriz que define el elemento estructural: Tiene un tamaño
muy inferior al tamaño de la matriz original que define la
imagen a la que modificará

5. DILATACIÓN
Dilatación: Se adiciona píxeles al contorno de
objetos presentes en la imagen
Píxel de salida: Máximo de los píxeles presentes en
la vecindad definida por el elemento estructural
1 0 0
0 0 0
0 0 0
1 1 1
1 1 1
1 1 1
1 0 0
0 1 0
0 0 0
Imagen de entrada Elemento estructural Imagen de salida

6. DILATACIÓN
Pasos para aplicarla dilatación
1.- Seleccionar el píxel de la imagen original a tratar
2.- Buscar el mayor de los píxeles de la vecindad, incluido el central, definidos por la forma y
tamaño del elemento estructural
3.- Sustituir el valor del píxel por el máximo valor
Los anteriores pasos se ejecutan para todos los píxeles de la imagen

7. EJEMPLO DE DILATACIÓN
I = imread('C:UserspersonalDocumentsMATLABMORFOLOGIabota.JPG');
se = strel('square',10);%crea un elemento que esta estructurado con una anchura de
10pixeles
I2 = imdilate(I,se);
imshow(I), title('imagen Original')
figure, imshow(I2), title('imagen Dilatada')

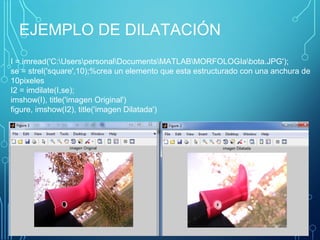
8. % Ejemplo de dilatación
% Imagen de entrada
I=[0 0 0 0 0 0 0;
0 0 0 0 0 0 0;
0 0 15 27 8 0 0;
0 0 100 95 1 0 0;
0 0 125 30 2 0 0;
0 0 0 0 0 0 0;
0 0 0 0 0 0 0];
imshow(imresize(I,[520,520])); %Se grafica la
matriz
% Se define el elemento estructural creando su
estructura morfologica
Ele=strel('square',3); %anchura de 3pixeles
% Se aplica dilatación
I1=imdilate(I, Ele);
figure;
imshow(imresize(I1,[520,520]));

9. EROSIÓN
Erosión: En imágenes binarias, elimina píxeles del
contorno de objetos presentes en la imagen
Píxel de salida: Mínimo de los píxeles presentes en
la vecindad definida por el elemento estructural
1 1 1
1 1 1
1 1 0
1 1 1
1 1 1
1 1 1
1 1 1
1 0 1
1 1 0
Imagen de entrada Elemento estructural Imagen de salida

10. EJEMPLO DE EROSIÓN
Si en el ejemplo anterior del programa MATLAB se sustituye
la función imdilate por imerode resulta:

11. % Ejemplo de erosion
% Imagen de entrada
I=[0 0 0 0 0 0 0;
0 0 0 0 0 0 0;
0 0 15 27 8 0 0;
0 0 100 95 1 0 0;
0 0 125 30 2 0 0;
0 0 0 0 0 0 0;
0 0 0 0 0 0 0];
imshow(imresize(I,[520,520])); %Se grafica
la matriz
% Se define el elemento estructural
CREANDO SU ESTRUCTURA
MORFOLOGICA
Ele=strel('square',3); %crea un elemento
que esta estructurado con una anchura de
3pixeles
% Se aplica erosion
I1=imerode(I, Ele);
figure;
imshow(imresize(I1,[520,520]));

12. DILATACIÓN VS EROSIÓN
Dilatación
Amplía bordes
Une objetos
próximos
Une puntos
blancos próximos
Elimina detalles
negros pequeños
Erosión
Reduce bordes
Separa objetos
próximos
Elimina puntos
blancos separados
Amplía detalles
negros pequeños

13. ELEMENTO ESTRUCTURAL
1 1 1
1 1 1
1 1 1
Origen del elemento estructural
Centro=(tamaño+1)/2
Para el elemento estructural cuadrado de tamaño
3x3 el centro será:
Centro={(3+1)(3+1)}/2=2x2
(3x3)

14. RECONSTRUCCIÓN
MORFOLÓGICA
La dilatación y la erosión poseen la particularidad de que
cuando iteran hasta estabilidad permiten la generación un
poderosos algoritmos de reconstrucción morfológica.
•APLICACIONES DE RECONTRUCCION MORFOLOGICA
Los resultados de la reconstrucción están fuertemente
influenciados por la elección correcta de la máscara y el
marcador.

15. REGIONES DE MEDICIÓN EN ESCALA
DE GRISES
(VER MATLAB)
Re g io npro ps función es muy útil para medir las
propiedades de los objetos en una imagen binaria
Pasos para obtención del resultado
Paso 1: Creación de Imagen Sintética
Paso 2: Crear una imagen binaria
Paso 3: Calcular Propiedades del objeto usando los
valores de píxeles de la imagen en escala de grises
Paso 4: Calcular personalizados píxel en función de valor
de propiedades

16. Podemos observar los valore obtenidos luego del
procesamiento en matlab aplicando la función
Regionprops

17. TRANSFORMADA DE LA DISTANCIA
La transformada de distancia proporciona una métrica
o medida de la separación de los puntos en la imagen.
La función bwdist calcula la distancia entre cada píxel
que está desactivado (0) y el píxel más cercano distinto
de cero para imágenes binarias.

18. EJEMPLO DE TRANSFORMADA DE
LA DISTANCIA
%TRANSFORMADA DE LA
DISTANCIA
center1 = -10;
center2 = -center1;
dist = sqrt(2*(2*center1)^2);
radius = dist/2 * 1.4;
lims = [floor(center1-1.2*radius)
ceil(center2+1.2*radius)];
[x,y] = meshgrid(lims(1):lims(2));
bw1 = sqrt((x-center1).^2 + (y-
center1).^2) <= radius;
bw2 = sqrt((x-center2).^2 + (y-
center2).^2) <= radius;
bw = bw1 | bw2;
figure, imshow(bw), title('bw')
D = bwdist(~bw);
figure, imshow(D,[]), title('trans
distancia en ~bw')

19. OPERACIONES COMPUESTAS:
TRANSFORMADA DE GANANCIA O
PÉRDIDA (HIT-OR-MISS)
Se define por la siguiente expresión:
)()( 21 BerosiónABerosiónABA c
−−∩−−=⊗
Imagen Complemento
de la imagen
Elemento
Estructural 1
Elemento
Estructural 2
Operación AND de la imagen, erosionada con un elemento
estructural y el complemento de la imagen, erosionada con
otro elemento estructural

20. OPERACIONES LÓGICAS
ENTRE IMÁGENES
>> III=I&II; (AND)
>> IV=I|II; (OR) >> V=~II;(NO)
>> VI=II&~I;(Diferencia)I
II

21. OBTENCIÓN DEL PERÍMETRO
Sustracción a la imagen la erosión de la imagen
)()( BerosiónAAAP −−−=
>>ee = strel('diamond',3)
>>bw1=imerode(bw, ee);
>>bw2=bw-bw1;
El perímetro puede ser más
delgado en función del
elemento estructural
que se utilice

22. OBTENCIÓN DEL PERÍMETRO (II)
Sustracción a la dilatación de la imagen la erosión
de la propia imagen
>>I1=imdilate(I,ee);
>>I2=imerode(I,ee);
>>I3=imsubtract(I1,I2);

23. OBTENCIÓN DEL PERÍMETRO (IV)
>>III=im2bw(II,.7);
>>IV=bwperim(III,8);
Conectividad

24. FUNCIÓN BWMORPH
BW2 = bwmorph(BW1,Operación,Número de veces que se repite)
Operaciones descritas previamente
'dilate‘
'erode‘
'open‘
'close‘
'skel’
Otras operaciones
‘bothat‘: Transformación bottom hat
‘tophat‘: Transformación top hat
‘clean’: Elimina píxeles aislados
‘fill’: Rellena píxeles interiores aislados

25. Elimina píxeles interiores aislados
Aplicación: Limpiar imagen
Función bwmorph(‘clean’)
>> B=bwmorph(A,’clean');
A =
0 0 0
0 1 0
0 0 0
B =
0 0 0
0 0 0
0 0 0

26. Elimina píxeles interiores de una vecindad
Aplicación: Obtener perímetro
Función bwmorph(‘remove’)
>> B=bwmorph(A,’remove');
A =
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
B =
1 1 1 1 1
1 0 0 0 1
1 0 0 0 1
1 0 0 0 1
1 1 1 1 1
Imagen original Aplicación remove