Este documento explica cómo calcular el dominio y rango de diferentes tipos de funciones, incluyendo funciones polinómicas, racionales, irracionales, exponenciales, logarítmicas y combinadas. El dominio de una función es el conjunto de todos los valores que la variable independiente puede tomar, mientras que el rango es el conjunto de todos los valores que la función puede producir.

1. Dominiode unafunción:
El dominiode unafunciónf ( x ) esel conjuntode todoslosvalorespara loscualeslafunción
estádefinida
Rango de una función:
El rango de la funciónesel conjuntode todoslosvaloresque f toma.
Calcular dominio y rango en funciones polinomicas
Aquellasfuncionescuyaexpresiónalgebraicaesunpolinomio,esdecir,lasfunciones
polinómicas,tienencomodominiotodoel conjuntode losnúmerosreales:R.
Ejemplo
DeterminarDominioyRangode
f(x) = X + 3
Comoes unafunciónlineal el dominioserátodoel conjuntode losnúmerosreales.
Dom f(x) =R
El Rango serátodoel conjuntode losnúmerosreales.Seguimosel eje “Y”de abajohacia arriba
y podemosleervaloressiempre.
Rango = (– ∞ , + ∞ )
Calcular dominio y rango en funciones racionales
Para calcularel dominiode este tipode funcionesel primerpasoesigualarel denominadora
cero y resolveresaecuación,unavezresueltaesaecuaciónel dominioestaráformadopor
todoslosrealesexceptolassolucionesde laecuación.

2. Ejemplo:
DeterminarDominioyRangode
Igualandoel denominadoracero:
X – 3 = 0 ; X = 3
El dominioestaráformadoportodoslosrealesexceptoel número3.
Dom f(x) =R – {3} ; (– ∞ , 3) U (3 , + ∞ )
Esta gráfica presentaunaasíntotahorizontal en“Y = 1”, Luegola funciónestarádefinidaen
todoslosvaloresde Y menosen“Y = 1”.
Rango = R – {1} ; (– ∞, 1) U (1 , + ∞ )
Calcular dominio y rango en funciones irracionales
Si el radical tiene índice impar,entoncesel dominioserátodoel conjuntoRde losnúmeros
realesporque al elegircualquiervalorde Xsiempre vamosapodercalcularlaraíz de índice
imparde laexpresiónque hayaenel radicando.
Perosi el radical tiene índice par,para losvaloresde Xque hagan el radicandonegativono
existirálaraíz y por tantono tendránimagen.Cuandoqueremoshallarel dominiode este tipo
de funcionesloprimeroque debemoshacerestomarloque hay dentrode la raíz y hacer que
seamayor o igual que cero.A continuaciónse resuelve esainecuaciónylasoluciónde dicha
inecuaciónconformael dominio de lafunción.
Ejemplo:

3. DeterminarDominioyRangode
f(x) =
Raíz de índice impar:
Dom f(x) =R
Rango = R
Calcular dominio y rango en funciones exponenciales
Al detectarque esuna funciónexponencial,podemosafirmarinmediatamente que :
Dom f(x) =R
Rango = ( 0 , + ∞ )

4. Calcular dominio y rango en funciones logarítmicas
El procedimientoparacalcularsudominioesbastante similaral de lasfuncionesirracionales.
Tomamoslo que haydentrodel logaritmoyhacemosque seamayor que cero.A continuación
resolvemoslainecuaciónylasoluciónnosdael dominio.
El Rango estarárepresentadoporel conjuntode todoslosnúmerosreales.
Ejemplo:
DeterminarDominio yRangode
f(x) =log(x+2)
X + 2 > 0 ; X > - 2
Dom f(x) =( – 2 , + ∞ )
Rango = R
Calculardominioyrangoen funciones combinadas
Ejemplo:
DeterminarDominioyRangode
f(x) =
Se nos presentaunafunciónracional que enel numeradorposee unafunción irracional.

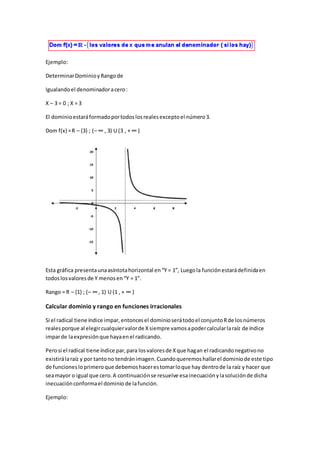
5. Para determinarel Dominiodebemosanalizarporseparadoel numeradoryel denominador.
Analizandoel numerador:
Comoel numeradoresuna raíz de índice par, lacantidadsub-radical oradicandotiene que ser
mayor o igual a cero
X + 2 ≥ 0 ; X ≥ 2
Analizandoel denominador:
Comola divisiónporceronoexiste,el denominadornuncapuede serigual acero.Luego:
Estos valoreslotrasladoa larecta real para visualizarmejorlosvaloresque se le pueden
asignara lavariable “X”y losmismos conformaránel Dominiode lafunciónestudiada,
Dom f(x) =[ -2 , + ∞ )
Graficamosahora la funciónparavisualizarsuRango:
Rango = [ 0 , 0.3535 ]