Este documento presenta un resumen de un libro de matemáticas básicas aplicadas a facultades de ciencias económicas y empresariales. El libro contiene 9 capítulos que cubren temas como incrementos y disminuciones porcentuales, ecuaciones, inecuaciones, funciones lineales y cuadráticas, funciones exponenciales y logarítmicas, límites y derivadas. El autor explica cada tema de manera clara y sencilla y proporciona numerosos ejercicios resueltos y propuestos



































![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
EJERCICIOS PROPUESTOS
I. Resuelva las ecuaciones siguientes :
1. 1+x=3-x 2. 2x - 5 = - 15 - 3x
3. 4(x - 3) = 8 - x 4. 2x - 5(1 - 3x) = 1 - 3(1 - 2x)
5. 3 - 2(1 - x) = 5 + 7(x - 3) 6. 6y - 5(1 + 2y) = 3 + 2(1 - y)
7. 3z - 2 + 4(1 - z) = 5(1 - 2z) - 12 8. 5[1 - 2(2z - 1)] = - 3(3z - 1) + 1
9. 1 - 2[4 - 3(x + 1)] = 4(x - 5) - 1
10. 3[2x + 1 - 2(2x - 1)] + 4 = 2[1 + 2(3 - x)]
3x + 7 1 + x 2x − 7 3x − 2
11. = 12. = 5−
2 3 3 4
5y − 6 2− y
13. = y− 14. 1/3 (2y + 1) + ½ y = 2/5 (1 - 2y) - 4
2 3
1 1 2z 1 3x − 5 4 − 5 x
15. 1 + 4 (3z − 1) = 3 − 2 16. =
2 4 4
4x + 1 2 − 3x 4 − 3x 5 − 3x 3 − 2 x
17. −8 = − 18. − =
3 3 10 5 10
4 − 2x 4 + x 3 + 4x 4 − 2x 3 − 7x 4x + 1 2x + 4
19. − + = + 20. + = 3−
24 8 3 24 16 8 16
Respuestas :
1. x=1 7. z = - 1 13. y=2 19. x = - 4/5
2. x=-2 8. z = 1 14. y = 122/59 20. x = 13
3. x=4 9. x = - 0 15. z=3
4. x = 3/11 10. x = - 2 16. x = 9/8
5. x = 17/5 11. x = -19/7 17. x = 21
6. y=-5 12. x = 94/17 18. x = 9/5
II. Resuelva las siguientes ecuaciones por la fórmula cuadrática.
1. x² + 3x + 1 = 0 2. x² - 4x + 2 = 0 3. 2x² + 3x - 4 = 0
4. 3x² + 6x - 2 = 0 5. x² + x - 3 = 0 6. 4x² - 12x + 9 = 0
29](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-37-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
SISTEMA SIMULTANEO DE 2 ECUACIONES CON 2 INCOGNITAS
Un sistema simultáneo de 2 ecuaciones lineales con 2 incógnitas es de la siguiente forma :
a1 x + b1 y = c1 (1)
a2 x + b2 y= c2 (2)
Aquí tenemos 2 ecuaciones [ (1) y (2) ] con 2 incógnitas ( x e y).
Ejemplo :
y + 3x = 5 El objetivo de este sistema de ecuaciones es determinar los valores de x e
4y - 5x = 3 y que satisfagan las dos igualdades. Para este sistema los valores que
satisfacen las igualdades son x = 1 y y = 2. veamos :
Reemplazando tenemos :
2 + 3 (1) = 5 5=5 Ok !
4 (2) - 5 (1) = 3 3=3 Ok !
¿Como se determina esta solución x = 1 y y = 2 ?
Para hallar la solución existen algunos métodos algebraicos para resolver el sistema. Estos
son :
1) Sustitución
2) Igualación
3) Reducción
Analicemos estos tres métodos :
1) SUSTITUCION
Consiste en despejar de cualquiera de las dos ecuaciones una variable (ya sea x ó y) y
reemplazarla en la otra ecuación restante, para que se genere una sola ecuación con una
incógnita. Veamos :
(1) y + 3x = 5
(2) 4y - 5x = 3 Despejamos “ y” de (1) y la reemplazamos en (2).
Entonces de (1) y = 5 - 3x si reemplazamos en (2) quedaría 4(5 - 3x) - 5x = 3
31](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-39-320.jpg)



![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
La solución definitiva serán 2 parejas :
x 1 = 15/4 ó x2 =1
y 1 = - 7/2 y2 = 2
6) Resolver el siguiente sistema :
y- x+2 =2 (1)
y2 - 8x = 0 (2)
Podemos resolver este sistema por sustitución. Entonces despejando la variable y de (1) y
reemplazarlo en (2) obtenemos :
De (1) → y=2+ x+2
Reemplazando en (2)
(2 + x + 2 )2 – 8x = 0 → 4 + 4 x + 2 + ( x + 2 )2 - 8x = 0
4 + 4 x + 2 + x + 2 – 8x = 0 → 4 x + 2 = 7x – 6 [elevando al cuadrado]
(4 x + 2 )2 = (7x – 6)2 → 16(x + 2) = 49x2 - 84x + 36
16x + 32 = 49x2 - 84x + 36 → 49x2 - 100x + 4 = 0
2
Resolviendo obtenemos : x1 = 2 ; x2 =
49
Hallar y1 ∧ y2 y decir que pareja de estas es la solución.
35](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-43-320.jpg)





![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
Observamos entonces que para ese nivel de producción el ingreso es igual al costo, o dicho
en otras palabras, en ese nivel de producción estamos en ! EQUILIBRIO !.
Esto indica que cubrir gastos es equivalente a estar en equilibrio.
Hemos determinado 2 valores de equilibrio : (2000 , 10’000000)
2000 Es el punto de equilibrio en unidades.
10’000000 Es el punto de equilibrio en unidades monetarias ($).
Hasta ahora en términos generales hemos definido lo siguiente :
CT = CV + CF → CT = (c.v.u) x + CF
I = p.x
Con esta información podemos hacer la siguiente formulación :
U = I - C → U = px - [(c.v.u) x + CF]
U = px - (c.v.u) x - CF
U + CF = px - (c.v.u) x (sacando a x como factor común)
U + CF = x ( p - c.v.u )
U + CF
=x → Esta es la expresión para hallar el nivel de producción para cualquier utilidad
p − c. v. u
En este ejercicio sabemos que : CF = 4’000000 p = 5000 c.v.u = 3000
o sea que la expresión quedaría así :
U + 4'000000 U + 4'000000
x = → x =
5000 − 3000 2000
41](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-49-320.jpg)









![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
17500 = 600x - 5x² ⇒ 5x² - 600x + 17500 = 0 (÷5)
x² - 120x + 3500 = 0 ⇒ a=1 b = - 120 c = 3500
− ( −120) ± ( −120) 2 − 4(1)(3500) 120 ± 400
x= ⇒ x=
2(1) 2
120 ± 20
x= ⇒ x1 = 70 ; x2 = 50
2
R/ Para que el ingreso sea de 17500 se deben producir y vender 50 ó 70 unidades.
[ I = p.x]
Si x = 70 ⇒ p = 600 - 5 (70) ⇒ p = 250 ⇒ I = 250 (70)
I = 17500
Si x = 50 ⇒ p = 600 - 5 (50) ⇒ p = 350 ⇒ I = 350 (50)
I = 17500
Nota : Podemos observar que en la medida en que la cantidad disminuye el precio aumenta
ó viceversa, (en la medida que el precio aumenta la cantidad disminuye).
b) p = ? ⇒ I = 18000 ⇒ Debo tener ingreso en término de p.
Para tener I(p) debo despejar a x en términos de p, veamos :
600 − p
p = 600 - 5x ⇒ 5x = 600 - p ⇒ x=
5
x = 120 - (1/5)p como I = px ⇒ I = p (120 - 1/5 p)
I(P) = 120p - 1/5 p²
Ahora reemplazo I = 18000
18000 = 120p - 1/5 p² ⇒ 1/5 p² - 120p + 18000 = 0
a = 1/5 = 0.2 b = - 120 c = 18000
51](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-59-320.jpg)







![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
EJERCICIOS RESUELTOS
Representar de las tres formas posibles las siguientes desigualdades.
a) x > 3 b) x ≤ 2/3 c) - 4 ≤ x < 5
R/
a) Gráficamente
0 3
Intervalo ⇒ S = ( 3 , +∞)
Comprensión ⇒ S = { x / x > 3}
b) Gráficamente
0 2/3
Intervalo ⇒ S = ( − ∞ , 2/3]
Comprensión ⇒ S = { x / x ≤ 23 }
c) Gráficamente
-4 0 5
Intervalo ⇒ S = [ -4 , 5 )
Comprensión ⇒ S = { x / −4 ≤ x < 5}
59](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-67-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
S = ( − ∞, - ½ ) ó S = {x / x < − 2}
1
-½ 0
3) Resolver :
5 - 3x ≥ 7 ⇒ - 3x ≥ 7 - 5
- 3x ≥ 2 (multiplicando por -1)
3x ≤ - 2 ⇒ x ≤ - 2/3
Nota : Siempre que una desigualdad se multiplique por -1 el sentido de esta cambia.
S = ( − ∞ , - 2/3 ] ó S = {x / x ≤ − 2}
3
- 2/3 0
4) Resolver :
2x − 5
≥2 ⇒ 2x - 5 ≥ 6 ⇒ 2x ≥ 11 ⇒ x ≥ 11/2
3
Nota : Dar la solución.
5) Resolver :
5 − 2x 4x − 7
< ⇒ 2 (5 - 2x) < 3 (4x - 7)
3 2
10 - 4x < 12x - 21 ⇒ - 4x - 12x < - 21 - 10
- 16x < - 31 (-1) ⇒ 16x > 31 ⇒ x > 31/16
Nota : Dar la solución.
61](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-69-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
2 + 3x 4 x − 5 2 − 3 x 5x
6) Resolver : − + ≤ −
12 3 4 3
− (2 + 3x ) + 4(4 x − 5) 3(2 − 3x ) − 20 x
≤ ⇒ - 2 - 3x + 16x - 20 ≤ 6 - 9x - 20x
12 12
13x - 22 ≤ - 29x + 6 ⇒ 13x + 29x ≤ 6 + 22 ⇒ 42x ≤ 28
x ≤ 28/42 ⇒ x ≤ 2/3
Nota : Dar la solución
EJERCICIOS PROPUESTOS
Resolver las siguientes desigualdades y dar la solución gráfica y mediante intervalo.
1) 4x - 2 > 6 R/ x > 2
2) 3x - 1 ≤ 8 R/ x ≤ 3
3x − 1
3) ≥4 R/ x ≥ 13/3
3
2 − 5x 4 x + 1
4) − ≥ R/ x ≥ 5/6
3 6
5) 3x - [2x - 3(6x + 1)] ≥ 2 - 5x R/ x ≥ - 1 /24
2( 3 − 5x 2 x − 1
6) − ≥ R/ x ≥ 21/34
3 4
2x − 1 3 − 2x 5 − 2 x 3x − 4
7) − ≥− + R/ x ≤ 19/9
15 3 5 3
2x + 3 3 − x 5 + 3x 5x
8) − + <− + R/ x > 13/28
18 9 9 3
62](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-70-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
Al final de cuentas gráficamente, tendríamos :
-5 3
De otra forma : S = ( - ∞, - 5 ] ∪ [ 3 , + ∞ ) ó S = { x / x ≤ −5} ∪ { x / x ≥ 3}
Nota : Debido a que la inecuación tiene el símbolo “ ≥ ” entonces tanto el - 5 como el
numero 3 son parte de la solución y se incluyen en esta. La inecuación anterior era de la
forma a.b ≥ 0 .
De que otra forma debe estar la inecuación para resolverla por el método anterior ?
R/ Para resolver por el método anterior se debe tener la inecuación de alguna de las formas
que a continuación se describe :
a a
1) ab ≥ 0 ó ab > 0 3) ≥0 ó >0
b b
a a
2) ab ≤ 0 ó ab < 0 4) ≤0 ó <0
b b
Cada una de estas formas podría extenderse a más factores ; por ejemplo :
1) abc ≥ 0 ó abcd. . . . z ≥ 0
abc abc
2) ≥0 ó <0
de de
Nota :
Se puede trabajar con cualquier número de factores, pero teniendo en cuanta que todos estos
se deben estar multiplicando entre sí.
65](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-73-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
( 9)(2) 9
iv) Si x = 3 ⇒ = − < 0 ! No sirve !
( −2)(5) 5
(13)(6) 78
v) Si x = 7 ⇒ = > 0 ! Sirve !
(2)(9) 18
-6 -2 1 5
S = ( - ∞, - 6 ] ∪ ( - 2 , 1 ] ∪ ( 5 , + ∞ )
Nota : Podemos observar que la desigualdad tiene el símbolo ≥ y sin embargo - 2 y 5 no
se incluye en la solución debido a que estos valores hacen que el denominador sea igual a
cero.
− 2( x − 3) 2
4) Resolver : ≥0
x ( x + 2)
Recordemos que ( x - 3 )2 = ( x - 3 ) ( x - 3 ) , si igualo cada uno de estos factores a cero,
el resultado será el mismo ( x = 3), por tanto se escogerá un solo factor de estos. Veamos :
x-3 =0 x=0 x+2 =0
x=3 x = -2 -2 0 3
− 2( −7) 2 − 2(49) 49
i) Si x = - 4 ⇒ = =− < 0 ! No sirve !
− 4 ( −2 ) 8 4
− 2( −4) 2 − 2(16)
ii) Si x = - 1 ⇒ = = 32 > 0 ! Sirve !
− 1(1) −1
− 2( −1) 2 − 2(1) 1
iii) Si x = 2 ⇒ = =− < 0 ! No sirve !
2( 4) 8 4
68](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-76-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
3 1
15) <4 16) ≥ 5
2x − 1 x
3 4 x 3 − 4x 2 + 4x
17) < 18) ≤0
x − 1 2x + 8 x −5
5x − 2 1 3 2x − 1
19) ≤ 20) ≥
x+3 2 8 x+2
Respuestas :
1. (- ∞ , -2] U [4 , + ∞ ) 11. [-8 , 3]
2. (- ∞ , -8) U (6 , + ∞ ) 12. [-6 , 0] U [3 , + ∞ )
3. (-1 , 3) 13. (-6 , 0) U (2 , 5)
4. [-5 , 1] 14. (- ∞ , -5) U (0 , 3]
5. [-4 , -2] U [5 , + ∞ ) 15. (- ∞ , 1/2) U (3/4 , + ∞ )
6. (- ∞ , -3] U [1 , 5] 16. (0 , 1/5]
7. (- ∞ , -3] U [0 , 5] 17. (- ∞ , -14] U (-4 , 1)
8. (-2 , 5) 18. [0 , 5)
9. [-3 , -1) U [5 , + ∞ ) 19. (-3 , 7/9]
10. [-2 , 3) 20. (-2 , 14/13]
71](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-79-320.jpg)







![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
CALCULO DE LA ECUACION DE LA LINEA RECTA
CONOCIDOS UN PUNTO P (X1, Y1) Y UNA PENDIENTE (m)
Supongamos que por un punto ya conocido P (x1, y1) pasa una línea recta cuya
pendiente (m) ya está dada. Esto es :
y
m : conocida
El puntoQ pertenece a la línea recta y tiene coordenadas
Q (x,y) Q (x, y). [cualquier punto que pertenezca a la línea recta
P (x1,y1) tiene coordenadas de la forma (x, y)].
x
Si calculamos la pendiente de la línea recta que pasa por P y Q, nos daría :
y − y1
m= → m (x - x1) = y - y1
x − x1
ó y - y1 = m (x - x1)
Esta es una expresión que sirve para calcular la ecuación de la línea recta dados un
punto P (x1 , y1 ) y una pendiente (m).
Esta fórmula es también denominada fórmula punto - pendiente
GRAFICA DE LA LINEA RECTA
Un segmento de recta lo podemos definir como la distancia mas corta entre 2 puntos.
Esto indica que para graficar una línea recta, lo podemos hacer únicamente ubicando
2 puntos en el plano cartesiano; estos 2 puntos pueden ser los interceptos con los
ejes. Para hallar estos interceptos se hace lo siguiente:
Intercepto con el eje y se hace x = 0 y se despeja y
Intercepto con el eje x se hace y = 0 y se despeja x
Ejercicio :
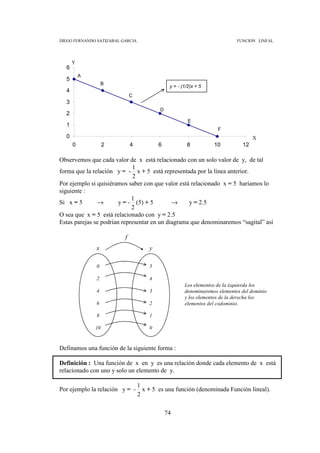
Hallar la ecuación de la recta que pasa por los puntos B (2,4) y E (8, 1) y graficarla.
1− 4 - 3 1
m= = → m = - → y - y1 = m (x - x 1 )
8−2 6 2
80](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-88-320.jpg)











![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
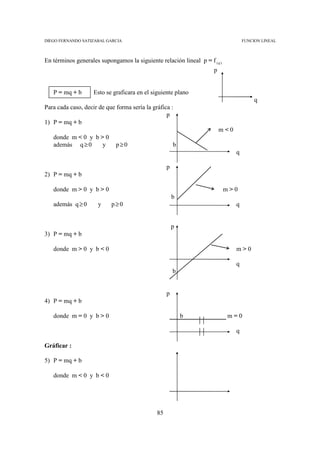
INTERPOLACION LINEAL
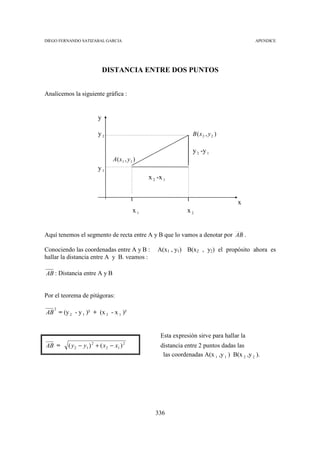
Revisando nuestras matemáticas básicas, si se tiene un segmento de recta AB donde
A(x1 , y1) y B(x2 , y2) como en el siguiente plano cartesiano :
y
A(x1 , y1) y1
Sabemos que la pendiente del segmento de
recta denotada por (m) la calculamos así :
y 2 − y1 y1 − y 2
m y2
= ó m=
B(x2 , y2) x 2 − x1 x1 − x 2
x1 x2 x
Lo anterior me dice que la pendiente se determina mediante la relación que existe entre la
diferencia de ordenadas y la diferencia de abscisas pero ¡Conservando el Orden!
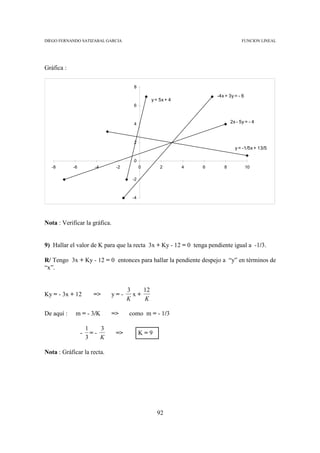
Supongamos que se tiene el siguiente segmento de recta en el plano cartesiano :
i[%]
A(20.5259 , 3.42)
3.42
C(20.7353 , i)
i
3.28 B(20.9479 , 3.28)
20.5259 20.7353 20.9479 Factor
Aquí se trata de determinar el valor de i para que el factor sea 20.7353.
¿Como se determina ?
R/ Se utiliza lo que se denomina interpolación lineal.
¿De qué forma ?
94](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-102-320.jpg)


































![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
C = Co + cYd → C = Co + c [ Y + TRo – tY]
C = Co + cY + cTRo – ctY → C = Co + cTRo + cY - ctY
Entonces : C = Co + cTRo + cY (1 – t)
C = Co + cTRo + c (1 – t)Y
Si llamamos c’ = c (1 – t) , donde c’ = Propensión marginal a consumir del ingreso total
Tendríamos :
C = Co + cTRo + c’Y C = f(Y)
Y = b + mx
Tengamos en cuenta que el intercepto con el eje de ordenadas es b = Co + CTRo y la
pendiente es m = c’ ó m = c (1 – t).
Con base en la siguiente ecuación c’ = c (1 – t) si analizamos detenidamente nos damos
cuenta que para que el valor de c’ aumente se requiere que c aumente ó t disminuya; y
viceversa, o sea, para que c’ disminuya se necesita que c disminuya ó que t aumente.
Resumen : ¿Cuando c’ ? → si c ó t
¿Cuando c’ ? → si c ó t
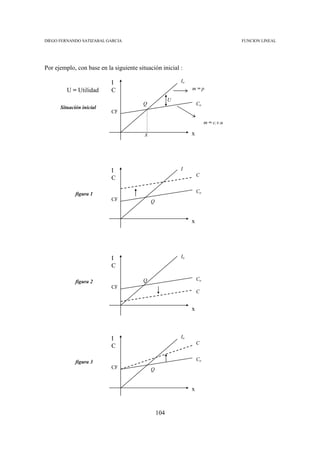
Gráficamente tenemos :
C = Co + cTRo + c’Y
C C
Co + CTRo Co + cTRo
Y Y
Figura 5 Figura 6
130](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-138-320.jpg)















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
h 1 h 1
i + bα i = α A - z → i( + bα ) = α A - z
k k k k
h + bkα 1
i
k =α A - kz
kα 1 M
iE = A− z Como z =
h + bkα h + bkα p
k α 1 M α
iE = A− Sea w =
h k h + bkα p k
1 + αb 1 + αb
h h
h 1 M
Entonces iE = wA − Este es el tipo de interés de equilibrio.
k h + bkα p
EJERCICIO RESUELTO
Dado : C = 90 + 0.65 yd L = 0.25y – 200i I = 150 – 100i
M
Go = 50 TRo = 150 t = 0.15 = 180
p
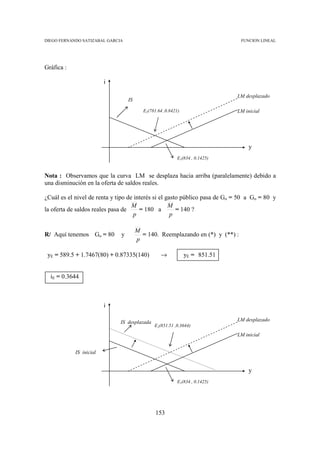
1) Hallar las ecuaciones de la curva IS y LM
2) Hallar las coordenadas del punto de intersección de las curvas IS y LM.
[o sea E(yE , iE)]
3) Hallar el nivel de producción y tipo de interés de equilibrio utilizando los
multiplicadores de política fiscal y monetaria.
Información :
Co = 90 Go = 50 c = 0.65 TRo = 150
k = 0.25 t = 0.15 h = 200 M /p = 180
Io = 150 b = 100
146](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-154-320.jpg)


















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION CUADRATICA
EJERCICIO RESUELTO
1) Por semana una compañía puede vender x unidades de su producto a un precio de p
dólares cada uno, en donde P = -0.5x + 1800. Si el costo de producción, para la
compañía es 600x + 420000 dólares por x unidades.
a. Graficar la función de ingreso I(x)
b. Graficar la función de utilidad U(x)
c. Cuántas unidades se deben producir para que el ingreso sea máximo ?
d. Cuántas unidades se deben producir para que la utilidad sea máxima ?
e. Para qué precio el ingreso será máximo ?
f. Para qué precio la utilidad será máxima ?
g. Cuál es el ingreso máximo ?
h. Cuál es la utilidad máxima ?
i. Hallar el costo en términos del precio.
j. Graficar utilidad en términos del precio.
K. Graficar en un solo plano cartesiano el ingreso en términos de p y costo en
términos de p y encontrar los puntos de intersección.
x = Cantidad [No. de unidades]
p = Precio de venta por unidad
p = - 0.5x + 1800
C(x) = 600x + 420000
Para graficar ingreso en términos de x debo tener I(x).
Recordemos que I = px
I = (- 0.5x + 1800) x
I(x) = - 0.5x² + 1800x donde a = - 0.5 b = 1800 c=0
Para hallar las coordenadas del vértice, hacemos :
b 1800
x= − => x= − => x = 1800
2a 2( −0.5)
166](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-174-320.jpg)







![DIEGO FERNANDO SATIZABAL GARCIA FUNCION CUADRATICA
El valor de p1 es el precio para que el ingreso sea máximo.
¿Como se determinó ?
R/ Para determinarlo debemos tener Ingreso en términos del precio [I(p)] y hallar
-b/2a.
O sea que si nos preguntan :
p=? para Imax debemos. →
tener
I(p) debemos. →
hallar
-b/2a
¿Como se determina el ingreso máximo ?
R/ Observemos que el ingreso máximo corresponde a la ordenada del vértice, o sea
b2
c-
4a
Si nos preguntaran :
Función de b2
Cuál es Imax = ? debemos. →
tener
debemos. →
hallar
c-
ingreso 4a
(cuadrática)
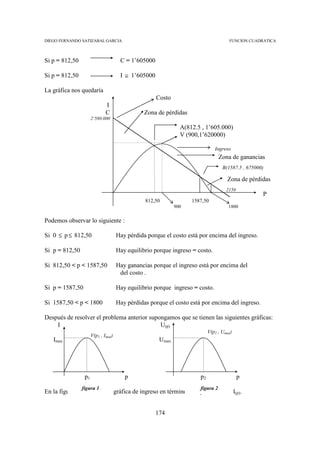
El análisis será idéntico para la figura 2 pero con la función de utilidad.
En el caso en que se tuvieran funciones de ingreso y utilidad en términos de q o sea :
I(q) y U(q) se haría de la misma forma.
Si la función es de costo (cuadrática) sería así:
C(x)
Cmin V(x1 , Cmin)
x1 x
175](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-183-320.jpg)





















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION EXPONENCIAL Y LOGARITMICA
Recordemos que para hallar f(9) debo reemplazar x = 9
f(9) = 5e9k → f(9) = 5 (e3k)3
Como e3k = 2 → f(9) = 5 (2)3 → f(9) = 5 (8) → f(9) = 40
Ejercicio :
La ecuación de demanda para cierto artículo es :
p
−
500
q = 400000 e Donde q = cantidad, p = precio por unidad ($)
a) Cuantas unidades se demandarán si el precio por unidad es de $2000 ?
b) Cuál debe ser el precio por unidad para que se demanden 20000 unidades.
c) Determinar el ingreso para el caso a y b.
d) Escribir la ecuación de ingreso en términos de p [I(p)]
e) Calcular el ingreso si el precio es de $2000
f) Escribir la ecuación de ingreso en términos de q [I(q)]
g) Calcular el ingreso si se demandan 20000 unidades.
Solución :
p
−
500
Sabemos que q = 400000 e
2000
−
a) q = ? si p = 2000 → q = 400000 e 500
q = 400000 e-4 → q = 400000 (0.018316) → q = 7326 unidades
b) p = ? si q = 20000
p p
− − 20000
20000 = 400000 e 500
→ e 500
=
400000
p
e
−
500
= 0.05 →
(ln)
-
p
= ln 0.05 → -
p
= -3
500 500
p = 1500 Precio por unidad
197](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-205-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA FUNCION EXPONENCIAL Y LOGARITMICA
c) Recordemos que I = pq
Para el caso (a) → I = 2000 (7326) → I = 14’652000
Para el caso (b) → I = 1500 (20000) → I = 30’000000
d) Sabemos que I = pq
p p
− −
500 500
Como q = 400000 e entonces I = p[400000 e ]
p
−
500
I(p) = 400000 p e Ingreso en términos de p.
e) Si p = 2000 → I=?
2000
−
I(2000) = 400000 (2000) e 500
→ I(2000) = 14’652511
Como I = pq entonces para hallar I(q) debemos despejar a p en términos de que de la
relación demandada, que es :
p p
− − q p q
q = 400000 e 500
→ e 500
= (ln) → - = ln
400000 500 400000
q q
- p = 500 ln (-1) → p = - 500 ln → p = f(q)
400000 400000
En conclusión, como I = pq entonces :
q q
I = (- 500 ln )q → I(q) = - 500 q ln
400000 400000
20000
g) Si q = 20000 → I(20000) = - 500 (20000) ln
400000
I(20000) = - 10’000000 (-3) → I(20000) = $ 30’000000
198](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-206-320.jpg)















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION EXPONENCIAL Y LOGARITMICA
39) Una cierta máquina industrial se deprecia hasta que su valor pasados t años es de
Q(t) = 11.000.000 e −0.4 t pesos. Cuánto tiempo habrá transcurrido para que su precio sea
$60.682 ?.
40) Una cierta maquinaria industrial se deprecia exponencialmente [F(x) = Ae − kx ] Si su
valor inicial en libros es de $12’000000 y de $1’983586 al cabo de seis años, calcule su
valor en libros después de 15 años.
41) Dada la siguiente relación :
x 2 − 2500
3 250
= 185.6p
( X = cantidad P = precio).
Hallar el ingreso total si P = 205.
42) Dada la siguiente relación :
x 2 − 3600
4 360 = 234.9p
Hallar el ingreso total si P = 205.
43) Para un cierto producto la ecuación de demanda es 50p = 300 e − x /1500
[x = # de unidades p = precio]
Calcular el ingreso cuando el precio por unidad es de $4.5
Respuestas :
1. x = 64 2. x = 5 3. x = 1/4
4. x = 16 5. x = 65 6. x = 3
7. x = ± 3 8. x = 4/3 9. x = 15/14
10. x = 3.7321 11. x = 2.3028 12. x = 1618.18
13. x = ± 2 14. x = 1 15. x = 1
16. x = - 1/9 17. x = - 2/17 18. x = 13/3
19. x = 0.1571 20. x = 2 21. x = 6.7767
214](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-222-320.jpg)




![3) lim[ f ( x ) ± g ( x ) ± ........ ± h( x ) ] = lim f ( x ) ± lim g ( x ) ± ....... ± lim h( x )
x −> a x −> a x −> a x − >a
a) lim (3x + 1) = lim 3x + lim 1 = 3 lim x + lim 1 = 3 (2) + 1 = 7
x −>2 x − >2 x − >2 x − >2 x − >2
b) lim (5x2 – 3x + 8) = lim 5x2 – lim 3x + lim 8 = 5 lim x2 – 3 lim x + lim 8
x − >3 x − >3 x − >3 x − >3 x − >3 x − >3 x − >3
= 5 (3)2 – 3 (3) + 8 = 44
Aquí estamos aplicando las propiedades, pero este limite lo podemos calcular más rápido
reemplazando inicialmente x = 3. Veamos :
lim (5x2 – 3x + 8) = 5 (3)2 – 3 (3) + 8 = 44
x − >3
4) lim[ f ( x ) .g ( x ) ....h( x ) ] = [ lim f ( x ) ].[lim g ( x ) ]......[ lim h( x ) ]
x −> a x − >a x−a x − >a
lim 4x2 . x3 = ( lim 4x2 ) . ( lim x3) = 4 (3)2 . (3)3 = 972
x − >3 x − >3 x − >3
f ( x) lim f ( x )
5) lim = x −> a
donde lim g ( x ) ≠ 0
x −> a g ( x) lim g ( x ) x −> a
x − >a
4 x − 1 lim (4 x − 1) 4(3) − 1 11
lim = x − >3 = = = 1
x − >3 2 x + 5 lim (2 x + 5) 2(3) + 5 11
x − >3
6) lim n f ( x ) = n lim f ( x )
x −> a x −> a
lim 3 4 x + 3 = 3 lim (4 x + 3) = 3 4(2) + 3 = 3
11
x −> 2 x − >2
219](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-227-320.jpg)




![x
3
si usted construye una tabla con los mismos valores de x por ejemplo para y = 1 +
x
se podrá dar cuenta de lo siguiente :
x
3
lim 1 + = e3
x − >∞
x
En términos generales podríamos decir que :
x k
r r
lim 1 + = er Análogamente : lim 1 + = er
x − >∞
x k − >∞
k
Si revisamos las matemáticas básicas nos damos cuenta que una de las propiedades de los
limites es la siguiente :
[ ]
lim f ( x )
x −> a
n
= [ lim f ( x ) ] n
x − >a
De acuerdo a esto, calcular :
nk
r
lim 1 + Aplicando la propiedad anterior.
k − >∞
k
n
r
nk
r
k
r
nk
lim 1 + = lim 1 + , Como lim 1 + = er entonces :
k −>∞
k k − > ∞ k
k −>∞
k
nk
r
lim 1 + = [er] n = ern
k −>∞
k
Conclusión :
nk
r
lim 1 + = ern
k −>∞
k
224](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-232-320.jpg)


![Recordemos que el exponente debe contener a 3x+4. Tratemos ahora de transformar la
expresión 2x-5 a una forma tal que contenga 3x+4.
¿Como lo haríamos ?
R/ Veamos :
3x 2 2
2x-5 ⇔ 2 - 5 ⇔ (3x) – 5 ⇔ (3x + 4 – 4) - 5
3 3 3
2 2 2 8 2 23
(3x + 4) - (4) – 5 ⇔ (3x + 4) - - 5 ⇔ (3x + 4) -
3 3 3 3 3 3
Podemos verificar que la expresión anterior es equivalente a 2x – 5, veamos :
2 23 6 8 23 15
(3x + 4) - = x+ - = 2x - ⇔ 2x - 5
3 3 3 3 3 3
2 23
(3 x + 4) −
2 3 3
lim 1 − sea z = 3x + 4
3 x + 4−>∞
3x + 4
2 23
z−
23 3
Entonces obtendríamos : lim 1 −
z −>∞
z
2 23
z −
23 2 3
= lim 1 − 1 − Aplicando propiedades tenemos :
z −>∞
z z
2 23 2/3
− −23 / 3
2 3 2
z
3 2 z 2
= lim 1 − lim 1 − = zlim 1 − . lim 1 −
z −>∞
z z − >∞ z − > ∞
z
z −>∞
z
= [e ]
−2 2 / 3
(1)-23/3 = e-4/3
227](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-235-320.jpg)

![CAPITULO 9
LA DERIVADA
En este capitulo vamos a definir e interpretar geométricamente la derivada, debido a que
esta tiene una aplicación muy amplia en las ciencias económicas y administrativas. Lo que
se va a exponer aquí no se hará con mucha rigurosidad debido a que la aplicación que se
requiere realmente no lo exige.
Construyamos el siguiente gráfico y posteriormente lo analizamos :
f(x)
f(x)
Recta secante
Recta secante
f(x2) Q
Recta tangente
P R
f(x1)
x
x1 x2
Consideremos la gráfica de una función f(x) donde cada uno de los puntos P[x1 , f(x1)] y
Q[x2 , f(x2)] pertenecen a ella.
229](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-237-320.jpg)




![1
Ahora si mN = − y M(3,9) entonces :
6
1 1 1 1 1
y–9 = − (x – 3) → y–9 = − x+ → y = − x+ +9
6 6 2 6 2
1 19
y = − x+ Ecuación de la recta Normal a la curva f(x) = x2 si x = 3.
6 2
En términos generales supongamos que se tiene una función y = f(x) y la gráfica es la
siguiente :
y
Recta tangente mt = f’(a)
P
f(a)
y = f(x)
Recta normal mN = - 1/f’(a)
a x
Con base en la gráfica anterior :
El punto P[a , f(a)] pertenece a la curva y = f(x) y por allí pasa una recta tangente. Para
determinar la pendiente de la recta tangente se debe calcular primero la derivada de la
función f(x) y posteriormente evaluarla en x = a esto es :
Si y = f(x) → hallar f’(x) y evaluar en x = a → mt = f’(a)
Como mt . mN = -1 y mt = f’(a) entonces :
1
f’(a) . mN = -1 → mN = − Pendiente de la recta normal
f '( a )
234](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-242-320.jpg)




![3
2) Si f(x) = ( - 4) (4 + 3 x ) hallar f’(x)
x2
Transformemos f(x) así : f(x) = (3x –2 – 4) (4 + 3x1/2)
3 –1/2
f’(x) = (3x –2 – 4). x + (4 + 3x1/2) (- 6x –3)
2
9 –5/2 27 –5/2
f’(x) = x – 6x –1/2 – 24x –3 – 18x –5/2 → f’(x) = - x – 6x –1/2 – 24x –3
2 2
27 6 24
f’(x) = - 5/2
− 1/ 2 − 3
2x x x
PROPIEDAD 6 : DERIVADA DEL COCIENTE DE 2 FUNCIONES
g ( x) h( x ) .g ' ( x ) − g ( x ) .h' ( x )
Si f(x) = donde h(x) ≠ 0 entonces f’(x) =
h( x ) [h( x ) ]2
Ejemplos :
x8
1) Si f(x) = 5 verificar que f’(x) = 3x2
x
Sea g(x) = x8 donde g’(x) = 8x7 y h(x) = x5 donde h’(x) = 5x4
Aplicando la propiedad tenemos :
x 5 (8 x 7 ) − x 8 (5 x 4 ) 8 x12 − 5 x12 3 x12
f’(x) = = = 10 → f’(x) = 3x2
(x5 ) 2 x10 x
Observemos lo siguiente :
x8
Si f(x) = esto es equivalente a tener f(x) = x3 y por supuesto f’(x) = 3x2
x5
Nota : Esto lo hicimos simplemente para ¡Verificar! que la propiedad se puede aplicar y
no se puede confundir esto con una ¡Demostración!.
239](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-247-320.jpg)
![3x 2 − 5
2) Si f(x) = hallar f’(x)
4 + 9x 2
Sea g(x) = 3x2 - 5 y h(x) = 4 + 9x2 aplicando la propiedad tenemos :
(4 + 9 x 2 )(6 x) − (3 x 2 − 5)(18 x) 24 x + 54 x 3 − 54 x 3 + 90 x
f’(x) = → f’(x) =
(4 + 9 x 2 ) 2 (4 + 9 x 2 ) 2
114 x
f’(x) =
(4 + 9 x 2 ) 2
DERIVADA DE UNA FUNCION COMPUESTA
(LA REGLA DE LA CADENA)
Anteriormente habíamos dicho que si teníamos por ejemplo y = x3 + 2x2 la derivada la
podíamos denotar de varias formas, y una de ellas era dy/dx que significa derivar a “y”
respecto a “x” y esto nos daría :
dy
Si y = x3 + 2x2 → = 3x2 + 4x
dx
En el caso por ejemplo que tuviéramos lo siguiente : y = u5 y además u = 3x2 – 5x
para estos casos podríamos hallar independientemente :
dy du
= 5u4 y = 6x - 5
du dx
Aquí tenemos dos funciones que se pueden componer en una sola, debido a que y = f(u) y a
la vez u = h(x) de tal forma que y = f[h(x)] esto es lo que se denomina una función
compuesta. Si aplicamos el concepto anterior tendríamos lo siguiente :
Si y = u5 y u = 3x2 – 5x podríamos mediante la composición de funciones
obtener :
y = (3x2 – 5x) 5 Aquí tenemos a “y” en términos de “x”
dy
¿Como podríamos obtener ?
dx
R/ Hasta ahora no hemos nombrado ninguna propiedad que nos permita hallar esta
derivada.
240](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-248-320.jpg)
![¿Que debemos hacer entonces ?
R/ Para hallar esta derivada utilizaremos la regla de la cadena.
¿En que consiste ?
R/ Como tenemos y = u5 y u = 3x2 – 5x podríamos hacer lo siguiente :
dy dy du dy
= . de tal forma que = 5u4 . (6x – 5)
dx du dx dx
dy
y como u = 3x2 – 5x entonces = 5 (3x2 – 5x)4 (6x – 5)
dx
Aquí podemos observar lo siguiente :
dy
Como y = (3x2 – 5x)5 para hallar se baja a multiplicar en este caso el número 5 y se
dx
deja la misma función pero elevada a la 4 (a 5 se le debe restar 1) y posteriormente se
multiplica por la derivada de la función que esta entre paréntesis (o sea 3x2 – 5x) que es
(6x – 5). A esta derivada se le conoce con el nombre de ¡Derivada Interna! En
conclusión:
dy
Si y = (3x2 – 5x)5 → = 5(3x2 – 5x)4 (6x – 5)
dx
¡Esta es la derivada interna!
En términos generales :
dy
Si y = [f(x)] n → = n [f(x)] n-1 . f’(x)
dx
Ejemplos :
dy
1) Si y = (x2 – 2x)3 hallar
dx
dy dy
= 3 (x2 –2x)2 (2x – 2) → = 3 (x2 –2x)2 . 2(x – 1) = 6 (x2 – 2x)2 (x – 1)
dx dx
dy
2) Si y= 3− t3 hallar
dt
241](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-249-320.jpg)
![dy 1 dy − 3t 2
y = (3 – t3)1/2 → = (3 – t3)-1/2 . (- 3t2) → =
dt 2 dt 2(3 − t 3 )1 / 2
dy 3t 2
= -
dt 2 3 − t3
5x 2 − 2
3) Si f(x) = hallar f’(x)
1 − 3x 2
Derivada Interna
1/ 2 −1 / 2
5x 2 − 2 1 5x 2 − 2 d 5x 2 − 2
f(x) =
1 − 3x 2
→ f’(x) =
2 1 − 3x 2
dx 1 − 3x 2
−n n
a b
Sabemos que = entonces :
b a
1/ 2
1 1 − 3x 2 (1 − 3 x 2 )10 x − (5 x 2 − 2)(−6 x)
f’(x) =
2 5x 2 − 2
(1 − 3 x 2 ) 2
1 (1 − 3 x 2 )1 / 2 [10 x − 30 x 3 + 30 x 3 − 12 x] (1 − 3 x 2 ) −3 / 2 − 2 x)
f’(x) = * → f’(x) =
2 (5 x 2 − 2)1 / 2 (1 − 3x 2 ) 2 2(5 x 2 − 2)1 / 2
x
f’(x) = -
(5 x − 2) (1 − 3 x 2 ) 3 / 2
2 1/ 2
dy
4) Si y= a2 − t2 donde a = constante, hallar
dt
dy 1 dy t
y = (a2 – t2)1/2 → = ( a2 – t2) -1/2 (-2t) → = -
dt 2 dt ( a − t 2 )1 / 2
2
dy t
= -
dt a −t2
2
2
5) Si y = - Hallar Dxy
(3 − 5 x 2 ) 4
80 x
y = - 2(3 – 5x2) –4 → Dxy = 8 (3 – 5x2) –5 (- 10x) → Dxy = -
(3 − 5 x 2 ) 5
242](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-250-320.jpg)

![DERIVACION IMPLICITA
Cuando teníamos por ejemplo y = 3x2 – 6x + 5 y queríamos hallar dy/dx nos quedaba
muy fácil puesto que la relación estaba escrita en forma explícita (o sea que la variable “y”
estaba ya despejada en términos de x), y esto nos daría dy/dx = 6x – 6.
Hay casos donde se tiene una relación escrita en forma implícita y de allí se requiere hallar
la derivada al respecto de una variable determinada y no es posible despejar la variable “y”
(por ejemplo) en términos de la otra variable. Veámoslo mediante un ejemplo:
dy
Dada 3y4x3 + 5y = 15 hallar :
dx
Si quisiéramos despejar a “y” en términos únicamente de x sería imposible debido a que al
tratar de despejar siempre me quedaría la variable “y” relacionada. Para hallar entonces
dy/dx debemos recurrir a la derivación implícita.
¿En que consiste ?
R/ Supongamos que y = f(x) y se quiere determinar ya sea y’ o f’(x). Procedemos de la
siguiente manera :
Como se tiene 3y4x3 + 5y = 15 haremos lo siguiente :
Se reemplazará y = f(x) y esto nos daría :
3[f(x)] 4 x3 + 5f(x) = 15 Ahora sí hallemos f’(x)
Recordemos que para derivar 3 [f(x)] 4 x3 es necesario aplicar la derivada de un producto.
Ahora si derivemos :
12 [f(x)] 3 f’(x) x3 + 3[f(x)] 4 3x2 + 5 f’(x) = 0
si reemplazamos f(x) = y , y además f’(x) = y’ tenemos :
12 y3 y’ x3 + 3y4 3x2 + 5y’ = 0 → 12 y3 y’ x3 + 5y’ = - 9y4x2
− 9y4x2
y’ (12y3x3 + 5) = - 9y4x2 → y’ =
12 y 3 x 3 + 5
Otra forma más sencilla de hallar y’ es la siguiente : como tenemos 3y4x3 + 5y = 15
derivaremos normalmente pero cuando derivemos la variable “y” la acompañaremos
(multiplicaremos) por y’ y posteriormente despejamos y’. Veamos :
244](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-252-320.jpg)



![dy 2(3 − 2 x ) + 2(2 x − 5) 6 − 4 x + 4 x − 10 dy 4
= = → = -
dx (2 x − 5)(3 − 2 x) (2 x − 5)(3 − 2 x) dx (2 x − 5)(3 − 2 x )
4 − x2 dy
4) Si y = ln Hallar
3x 2 + 5 dx
Antes de derivar podemos hacer la siguiente transformación :
1/ 2
4 − x2
y = ln 2
3x + 5
Recordemos que logb M n = n logb M , entonces :
1 4 − x2 1
y= ln 2
3x + 5
→ y= [ln (4-x2) – ln (3x2 + 5)]
2 2
Hasta ahora simplemente se hizo una transformación. Ahora si derivamos, observemos :
dy 1 1 1 1 − 2x 6x
= (−2 x ) − 2 (6 x) = 4 − x 2 − 3x 2 + 5
dx 2 4 − x 2
3x + 5 2
dy 1 − 2 x(3 x 2 + 5) − 6 x(4 − x 2 ) 1 − 6 x 3 − 10 x − 24 x + 6 x 3
= =
dx 2 (4 − x 2 )(3 x 2 + 5) 2 (4 − x 2 )(3 x 2 + 5)
dy 1 − 34 x dy 17 x
= → =-
dx 2 (4 − x )(3x + 5)
2 2
dx (4 − x )(3 x 2 + 5)
2
Consideremos ahora la siguiente función exponencial y = ax .
Para hallar y’ podemos hacer lo siguiente :
Si y = ax → ln y = ln ax → ln y = x ln a
Si derivamos implícitamente obtenemos (1/y) y’ = ln a , entonces y’ = y ln a , y
como
y = ax entonces :
y’ = ax ln a
248](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-256-320.jpg)



![1 1
Derivando implícitamente y’ = (1) ln (x2 + 5) + x 2 2x
y x +5
1 2x 2 2x 2
y’ = ln (x2 + 5) + 2 → y’ = y [ln (x2 + 5) + ]
y x +5 x2 + 5
2x 2
y’ = (x2 + 5)x [ln (x2 + 5) + ]
x2 + 5
2) Si y = xln x → ln y = ln xln x → ln y = ln x. ln x
ln y = (ln x)2 derivando implícitamente :
1 1 2 2
y’ = 2 (ln x)1 → y’ = y ln x → y’ = xln x ln x
y x x x
2 2
y = (2 x + 1) ln y = ln (2 x + 1)
ex ex
3) Si → → ln y = ex² ln (2x + 1)
Derivando implícitamente :
1 1 1 1
y’ = ex² . 2x . ln (2x + 1) + ex² 2 → y’ = 2 ex² [x ln (2x + 1) + ]
y 2x + 1 y 2x + 1
1 x2 1
y’ = y 2 ex² [x ln (2x + 1) + ] → y’ = 2 ex² ( 2 x + 1) e [x ln (2x + 1) + ]
2x + 1 2x + 1
DERIVADAS DE ORDEN SUPERIOR
Cuando teníamos por ejemplo y = x5 + 3x4 – 10x3 + 2x2 – 6 y determinábamos y’
estabamos hallando la primera derivada de la función y esto se podía denotar por dy/dx ó
Dxy por ejemplo.
Así como se determina la primera derivada, también se pueden hallar derivadas de orden
superior, que consiste en hallar por ejemplo la segunda derivada, tercera derivada, cuarta
derivada, etc.
252](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-260-320.jpg)

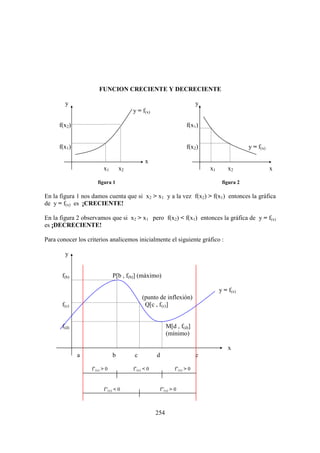
![FUNCION CRECIENTE Y DECRECIENTE
y y
y = f(x)
f(x2) f(x1)
f(x1) f(x2) y = f(x)
x
x1 x2 x1 x2 x
figura 1 figura 2
En la figura 1 nos damos cuenta que si x2 > x1 y a la vez f(x2) > f(x1) entonces la gráfica
de y = f(x) es ¡CRECIENTE!
En la figura 2 observamos que si x2 > x1 pero f(x2) < f(x1) entonces la gráfica de y = f(x)
es ¡DECRECIENTE!
Para conocer los criterios analicemos inicialmente el siguiente gráfico :
y
f(b) P[b , f(b)] (máximo)
y = f(x)
(punto de inflexión)
f(c) Q[c , f(c)]
f(d) M[d , f(d)]
(mínimo)
x
a b c d e
f’(x) > 0 f’(x) < 0 f’(x) > 0
f”(x) < 0 f”(x) > 0
254](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-262-320.jpg)
![Supongamos que se tiene la gráfica de una función y = f(x) definida en el intervalo [a,e].
Con base en esta gráfica se pueden hacer los siguientes comentarios :
1) En el intervalo [a , b) y (d , e] la gráfica de f(x) es creciente.
2) En el intervalo (b , d) la gráfica de f(x) es decreciente.
3) Cualquier recta tangente a la curva f(x) en el intervalo [a , b) ó (d , e] tiene pendiente
positiva.
4) Cualquier recta tangente a la curva f(x) en el intervalo (b , d) tiene pendiente negativa.
Nota : Como la derivada corresponde a la pendiente de la recta tangente entonces podemos
decir que tener una pendiente de una recta tangente positiva, es equivalente a tener una
derivada positiva.
En conclusión si la gráfica de una función en un determinado intervalo es creciente
entonces la derivada en ese intervalo será positiva.
Análogamente, si la gráfica de una función en un determinado intervalo es decreciente
entonces la derivada es negativa. O sea que podemos establecer el siguiente criterio de
primera derivada así :
CRITERIOS DE LA PRIMERA DERIVADA
Si f’(x) > 0 en (a , b) entonces f(x) es creciente en (a , b)
Si f’(x) < 0 en (b , d) entonces f(x) es decreciente en (b , d)
Si f’(x) > 0 en (d , e) entonces f(x) es creciente en (d , e)
Si observamos la gráfica nos damos cuenta que el punto P[b , f(b)] es un punto máximo y
el punto M[d , f(d)] es un punto mínimo.
El punto máximo ocurre cuando x = b y el punto mínimo ocurre cuando x = d.
Los valores x = b y x = d se llaman valores ó puntos críticos. En consecuencia un
valor crítico es aquel donde existe un máximo ó un mínimo. En el punto máximo o mínimo
la pendiente de la recta tangente es igual a cero (o sea que en estos puntos f’(x) = 0).
Para determinar los valores críticos (x = b y x = d) se debe derivar f(x) y posteriormente
igualar a cero.
O sea dada y = f(x) DERIVAR →
f’(x) IGUALAR. A.CERO →
f’(x) = 0 DESPEJAR→
x
El valor máximo está en x = b. ¿Cuál es este valor máximo ?
255](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-263-320.jpg)
![R/ El valor máximo es f(b) .
El valor mínimo está en x = d y este valor es f(d).
La gráfica de f(x) es cóncava hacia abajo en el intervalo (a , c) y cóncava hacia arriba en el
intervalo (c , e).
CRITERIOS DE LA SEGUNDA DERIVADA
Si f”(x) < 0 en (a , c) entonces f(x) es cóncava hacia abajo en (a , c)
Si f”(x) > 0 en (c , e) entonces f(x) es cóncava hacia arriba en (c , e)
En el punto Q[c , f(c)] la gráfica de f(x) pasa de ser cóncava hacia abajo a cóncava hacia
arriba.
El punto Q se llama punto de inflexión. En consecuencia un punto de inflexión es un punto
donde la concavidad de una curva cambia.
¿Para que valor de x hay un punto de inflexión ?
R/ Para x = c.
¿Como se determina este valor ?
R/ Para determinar este valor se debe hacer f”(x) = 0.
Habíamos dicho que los valores críticos son aquellos donde existe un máximo ó un
mínimo. Es muy probable que se tenga en algunos casos más de un valor critico y se quiera
saber si cada uno de estos valores corresponde a un máximo ó a un mínimo. Para esto existe
un Teorema que lo podemos enunciar así :
Sea y = f(x) una función definida en [a , b] donde m ∈ [a , b], si x = m es un valor
crítico y :
f”(m) > 0 entonces x = m corresponde a un mínimo y si
f”(m) < 0 entonces x = m corresponde a un máximo.
Ahora podemos definir cuales podrían ser los pasos a seguir para graficar una función f(x) ,
utilizando los criterios de primera y segunda derivada.
Pasos :
1) Calcular f’(x).
256](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-264-320.jpg)
![2) Hallar valores críticos. ¿Cómo? R/ Haciendo f’(x) = 0 y despejando x.
3) Ubicar los valores máximos y/o mínimos. ¿Cómo? R/ Reemplazando en la función
original [f(x)] los valores hallados en el numeral 2.
4) Determinar los posibles puntos de inflexión. ¿Cómo? R/ Haciendo f”(x) = 0
despejando x y reemplazando estos valores en la función original [f(x)].
5) Ubicar los valores críticos (numeral 2) y el valor donde existe el posible punto de
inflexión (numeral 4) en una recta numérica, para analizar signos de primera y segunda
derivada.
6) Graficar, dependiendo de los signos hallados en el numeral 5.
Nota : Expliquemos como se siguen estos pasos mediante un ejemplo :
Ejemplo :
Graficar utilizando criterios de 1ra y 2da derivada la siguiente función :
1 3
f(x) = x – 3x2 + 5x + 2
3
Pasos :
1) f’(x) = x2 – 6x + 5
2) ¿Valores críticos ? → f’(x) = 0
x2 – 6x + 5 = 0 → (x – 1) (x – 5) = 0 → x–1=0 ∨ x–5=0
x=1 ∨ x=5
3) Ubicar puntos :
1 13
Si x=1 → f(1) = (1)3 – 3(1)2 + 5(1) + 2 → f(1) = (1 , 13/3)
3 3
1 19
Si x=5 → f(5) = (5)3 – 3(5)2 + 5(5) + 2 → f(5) = - (5 , -19/3)
3 3
4) ¿Puntos de inflexión? → f”(x) = 0
Como f’(x) = x2 – 6x + 5 entonces f”(x) = 2x – 6 :
2x – 6 = 0 → 2x = 6 → x=3
257](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-265-320.jpg)



![e −2 x
11) y = e –x 12) y =
x
2 e x + e−x
13) y = ln (x4 + e x ) 14) y =
e x − e −x
ln x
15) y = ln e x + e−x 16) y =
ex
1 + e2x 1 − e−x
17) y = ln 18) y = ln
1 − e2x ex
1/ 3
x−3 1 − 3e −2 x
19) y = log5 20) f(x) = log −2 x
2x − 1 2+e
PROBLEMAS DE OPTIMIZACION
(Ver ejercicios resueltos de aplicación en el capítulo de Aplicación a Microeconomía)
Observemos las siguientes gráficas :
V(x) CMe
CMe(q)
Vmax V(x)
CMemin
x1 x q1 q
figura 1 figura 2
Supongamos que x = longitud (mts) ; V = Volumen (m3) ; q1 = Cantidad
CMe = Costo medio total.
Aquí nos damos cuenta que en la figura 1 para que el volumen sea máximo la longitud
debe ser x1.
x1 es un valor crítico.
¿Como se determina x1 ?
R/ Para determinar x1 debemos tener V(x) posteriormente derivar [V’(x)] e igualar a cero,
para despejar a x1.
261](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-269-320.jpg)









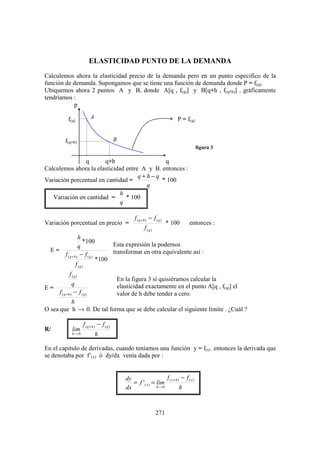
![ELASTICIDAD PUNTO DE LA DEMANDA
Calculemos ahora la elasticidad precio de la demanda pero en un punto especifico de la
función de demanda. Supongamos que se tiene una función de demanda donde P = f(q).
Ubiquemos ahora 2 puntos A y B, donde A[q , f(q)] y B[q+h , f(q+h)] , gráficamente
tendríamos :
p
f(q) A P = f(q)
f(q+h) B
figura 3
q q+h q
Calculemos ahora la elasticidad entre A y B. entonces :
q+h−q
Variación porcentual en cantidad = * 100
q
h
Variación en cantidad = * 100
q
f ( q+ h) − f ( q)
Variación porcentual en precio = * 100 entonces :
f (q)
h
* 100
q Esta expresión la podemos
E= transformar en otra equivalente así :
f ( q+h) − f (q)
* 100
f (q)
f (q)
En la figura 3 si quisiéramos calcular la
q elasticidad exactamente en el punto A[q , f(q)] el
E=
f ( q+h) − f (q) valor de h debe tender a cero.
h
O sea que h → 0. De tal forma que se debe calcular el siguiente límite . ¿Cuál ?
f (q+ h) − f ( q)
R/ lim
h −>0 h
En el capitulo de derivadas, cuando teníamos una función y = f(x) entonces la derivada que
se denotaba por f’(x) ó dy/dx venía dada por :
dy f ( x+ h) − f ( x )
= f ' ( x ) = lim
dx h − >0 h
271](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-279-320.jpg)








![4
Esto indica que p= tiene elasticidad unitaria para todos los valores de q donde
q
q > 0. Si analizamos en términos generales una función de la forma p = c / q donde
c = constante.
dp dp c
Entonces p = c . q-1 → = - c q-2 → = - 2
dq dq q
c
p q c
q q q2
Como E = → E= = → E=-1
dp c c
− 2 − 2
dq q q
En conclusión, toda función de demanda de la forma p = c / q (llamada hipérbola lateral)
donde q > 0 tiene elasticidad unitaria para todos sus valores de q.
EJERCICIOS PROPUESTOS
A continuación se da una función de demanda donde p = f(q) ó q = f(p). para cada caso se
debe graficar la función en el primer cuadrante y decir para que valores de p y de q está
definida. Además se debe determinar para que valores de q y p la demanda tiene
elasticidad unitaria e indicar la región donde la demanda es elástica e Inelástica. Hallar la
elasticidad para 2 valores de p ó de q donde la demanda es elástica e Inelástica.
1) p = - (1/50)q + 2000 2) p = - 2q + 80
3) p = - (1/4000)q2 + 600 4) q = - (1/5) p2 + 80000
5) p=5/q 6) p = 300 / q2
7) q = 200 – 4p 8) x = 40 (5 - p )
9) x = 200 (4 – p) 10) x = 400 16 − p
ANALISIS MARGINAL
El objetivo ahora va a ser aplicar la derivada a la economía en lo que tiene que ver con las
tasas marginales, donde es muy útil hablar de costo marginal, ingreso marginal, utilidad
marginal, etc.
Para comprender por ejemplo el concepto de costo marginal supongamos inicialmente que
se tiene una función de costo total definida por la siguiente ecuación :
C(x) = 0.05 x2 + 2500 ; x ≥0 donde x = cantidad
C = costo total [$]
Esta es una función cuadrática donde la gráfica es una parábola y como a > 0 entonces
abre hacia arriba. El vértice tiene coordenadas V(0 , 2500) y la gráfica quedaría así :
280](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-288-320.jpg)



![Para el caso (b) producir el artículo No. 1001 cuesta aproximadamente $100.
Para el caso (c) producir el artículo No. 2001 cuesta aproximadamente $200.
Ejemplo:
Supongamos que se tiene la siguiente función de costo C(x) = 0.002x3 – 1.2x2 + 265x+500,
Se pide :
a) Determinar el costo marginal en función de x.
b) Evaluar el costo marginal si i) x = 150 ii) x = 200 iii) x = 250
c) Graficar el costo marginal [o sea C’(x)]
dc
R/ El costo marginal viene dado por ó C’(x) , entonces :
dx
Si C(x) = 0.002x3 – 1.2x2 + 265x+500
a) C’(x) = 0.006x2 – 2.4x + 265 Este es el costo marginal.
b) Si x = 150 → C’(150) = 0.006(150)2 – 2.4(150) + 265 → C’(150) = 40
Si x = 200 → C’(200) = 25
Si x = 250 → C’(250) = 40
Esto nos indica que cuando se producen 150 unidades producir un articulo adicional cuesta
$40; cuando se producen 200 unidades producir un articulo adicional cuesta $25 y cuando
se producen 250 unidades producir un articulo adicional cuesta $40.
c) Si vamos a graficar C’(x) nos damos cuenta que esta es una función cuadrática, donde el
valor de a > 0 o sea que la parábola abre hacia arriba. Veamos :
C’(x) = 0.006x2 – 2.4x + 265 a = 0.006 b = -2.4 c = 265
b − (−2.4)
x=- = = 200 si
2a 2.(0.006)
Si x = 200 C’(200) = 0.006(200)2 – 2.4(200) + 265 → C’(200) = 25
Vértice → V(200,25) Intercepto con el eje C’(x)
Si x=0 → C’(0) = 0.006 (0)2 – 2.4 (0) + 265 → C’(0) = 265
284](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-292-320.jpg)



![Ejercicio Resuelto :
Supongamos que para un fabricante la relación de demanda viene dada por :
1
p = - x + 3000 donde p = precio, y x = cantidad. Los costos fijos los estima en
2
$500000 y el sabe que producir cada artículo le cuesta $1000. Se pide :
1) Hallar la función de ingreso en términos de x.
2) Hallar la función de utilidad en términos de x.
3) Graficar la función de utilidad U(x) y hallar el nivel de producción para que la utilidad
sea máxima.
4) Hallar el precio por articulo que permite la máxima utilidad.
R/ 1) Para hallar I(x) recordemos que Ingreso = (precio) (cantidad) ; I = p.x ;
1 1 1 2
como p = - x + 3000 entonces I = (- x + 3000) x → I(x) = - x + 3000x
2 2 2
2) Recordemos que Utilidad = ingreso – Costo , o sea que U(x) = I(x) – C(x)
y como CT = CV + CF , sabemos que costo variable unitario = $1000.
Costos fijos = $500000. Entonces C = 1000x + 500000 , ahora si :
1
I(x) = - x2 + 3000 x y C(x) = 1000x + 500000
2
1 1
U(x) = - x2 + 3000 x – (1000x + 500000) → U(x) = - x2 + 3000 x – 1000x - 500000
2 2
1
U(x) = - x2 + 2000 x - 500000
2
1 2
3) Teniendo U(x) = - x + 2000 x – 500000 podemos utilizar los criterios de derivada
2
para graficar, así :
1er Paso : Hallar U’(x) = - x + 2000
2do Paso : Determinar valores críticos [haciendo U’(x) = 0].
Si U’(x) = 0 → - x + 2000 = 0 → x = 2000 Aquí hay un máximo o un mínimo
1
Si x = 2000 → U(2000) = - (2000)2 + 2000 (2000) – 500000
2
U(2000) = 1’500000
Ya tenemos un punto de coordenadas (2000 , 1’500000).
288](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-296-320.jpg)
![3er Paso : Hallar U”(x)
Como U’(x) = - x + 2000 → U”(x) = - 1 Esto indica que la parábola abre hacia abajo
[porque U”(x) < 0]
¿Como se determinan los interceptos con el eje x ?
1
R/ Haciendo U = 0 , Como U(x) =- x2 + 2000 x – 500000 , si U= 0
2
1 2 1 2
0 = - x + 2000 x – 500000 (-1) → x - 2000 x + 500000 = 0
2 2
Solucionando esta ecuación obtenemos x1 = 3732 x2 = 268
La gráfica quedaría así :
U(x)
V (2000 ,1’500000)
1’500000
U(x) = - (1/2)x2 + 2000x - 500000
x
268 2000 3732
U’(x)
2000
U’(x) = - x + 2000
x
2000
Tengamos en cuenta que si U’(x) = - x + 2000 entonces los interceptos se hallan así :
Si x = 0 → U’(0) = 2000
Si U’ = 0 → 0 = - x + 2000 → x = 2000
289](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-297-320.jpg)
![Aquí se ha graficado la función de utilidad total U(x) en un plano cartesiano y la función de
utilidad marginal U’(x) en otro; de tal forma que el nivel de producción para que la
utilidad sea máxima debe ser de x = 2000 unidades y si observamos la gráfica de utilidad
marginal ésta corta el eje de abscisas (eje x) en este nivel de producción (x = 2000).
1
Para determinar el precio para utilidad máxima sabemos que p = - x + 3000 entonces si
2
1
x = 2000 reemplazando obtenemos p = - (2000) + 3000 → p = $ 2000
2
Este es el precio por unidad para que la utilidad sea máxima
Respondamos ahora la siguiente pregunta :
¿Cómo se determinó el nivel de producción para que la utilidad fuera máxima ?
R/ Para determinar este valor (x = 2000) se igualó la utilidad marginal [U’(x)] a cero, y se
despejo x (valor critico). O sea que U’(x) = 0 y se despejó x.
sabemos que U(x) = I(x) – C(x) si derivamos :
U’(x) = I’(x) – C’(x) si igualamos U’(x) = 0
0 = I’(x) – C’(x)
C’(x) = I’(x) Esto indica que hacer U’(x) = 0 es equivalente a
igualar costo marginal e ingreso marginal.
Dicho en otras palabras, para determinar el nivel de producción o precio para que la utilidad
sea máxima se debe igualar la utilidad marginal a cero [U’(x) = 0] ó igualar el ingreso
marginal y el costo marginal [C’(x) = I’(x)].
UTILIDAD MARGINAL = 0
PARA MAXIMIZAR UTILIDAD → ó
INGRESO MARGINAL=COSTO MARGINAL
Por ejemplo, en el caso anterior tenemos :
1
I(x) = - x2 + 3000x → I’(x) = - x + 3000
2
C(x) = 1000x + 500000 → C’(x) = 1000
Entonces para maximizar utilidad I’(x) = C’(x) :
- x + 3000 = 1000 → 3000 – 1000 = x → x = 2000 Nivel de producción para Umax
290](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-298-320.jpg)








![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
Por ejemplo :
(x + 5)2 - (4 - 2x)2 = [x + 5 - (4 - 2x)] [x + 5 + (4 - 2x)]
( ) = (x + 5 - 4 + 2x) (x + 5 + 4 - 2x)
X+5 4-2x = (3x + 1) (9 - x)
Tengamos en cuenta lo siguiente :
a2 + b2 ≠ (a + b) (a + b)
Factorizar :
-25 + x2 → Es conveniente ordenarlo así x2 - 25
x2 - 25 = (x - 5) (x + 5)
1) m2 - 4 = ( - )( + )
2) z2 - 49 = ( )( )
3) (x + 3)2 - 81 =
4) (z - 2)2 - (2 + 4z)2 =
5) (m + 2x)2 - (x - 3m)2 =
DIFERENCIA Y SUMA DE CUBOS
1) a3 - b3 = (a - b) (a2 + ab + b2)
(3 )
a b
a3 + b3 = (a + b) (a2 - ab + b2)
Ejemplos :
1) x3 - 8 = (x - 2) (x2 + 2x + 4)
x 2
299](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-307-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
2) m3 + 27 = (m + 3) (m2 - 3m + 9)
m 3
3) 8z3 - 125 ↔ (2z)3 - (5)3 = (2z - 5) [(2z)2 + 2z (5) + (5)2]
2z 5 = (2z - 5) (4z2 + 10z + 25)
Nota : Debemos tener en cuenta que la expresión a2 ± ab + b2 no es factorizable.
En términos generales :
3 ± 3= ( ± )( 2 m + 2)
Factorizar :
1) (m + 1)3 - 64 = (m + 1 - 4) [(m + 1)2 + 4 (m + 1) + (4)2]
= (m - 3) (m2 + 2m + 1 + 4m + 4 + 16)
m+1 4
= (m - 3) (m2 + 6m + 21)
2) n3 - 64 =
3) 8a3 + 27m3 =
4) 27(a - 3)3 - 8a3 =
TRINOMIO CUADRADO PERFECTO
Recuerde que (a ± b)2 = a2 ± 2ab + b2
Ejemplos :
1) ( x + 5)2 = x2 + 2x(5) + (5)2
= x2 + 10x + 25
300](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-308-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
1) x2 - 10x = x2 - 10x + 25 - 25
2
10
= 25 = (x - 5)2 - 25
2
2) x2 - 18x =
3) m2 + 14m =
4) z2 - 16z =
5) 3x2 - 18x → Debo factorizar primero el coeficiente de x2
3( x2 - 6x) → 3 [x2 - 6x + 9 - 9]
3 [(x - 3)2 - 9] = 3 (x - 3)2 - 27
6) 2x2 - 16x =
7) 4m2 + 40m =
8) 5x2 - 60x =
TRINOMIO DE LA FORMA ax2 + bx + c
Casos : 1) Si a = 1 Ejemplo → x2 + 2x - 15
2) Si a ≠ 1 Ejemplo → 2x2 + 5x - 12
Para el primer caso a = 1 ¿cómo se factoriza x2 + 2x - 15 ?
Veamos :
x2 + 2x - 15 = (x + 5) (x - 3)
Se deben abrir dos (2) paréntesis cuya variable es “x”, los signos deben ir así : el signo del
primer paréntesis es el mismo signo de el coeficiente de x (o sea +) y el signo del segundo
paréntesis es el producto entre el signo del coeficiente de “x” y el signo del termino
independiente, o sea (+) . (-) = (-)
Signo del coeficiente de “x” Signo del término independiente
302](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-310-320.jpg)




![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
x 2 + xy + y 2
14) =
x2 y 2
−
y x
a a +1
−
15) a − 1 a =
a
1−
a −1
1 1
− 2
( x + h) 2
x
16) =
h
EJERCICIOS PROPUESTOS
1) Simplifique las siguientes expresiones :
a. 5 - (- 3) i. -7 - (-3)
b. (- 3) (- 7) j. 8 ÷ (-2)
c. - (- 4 - 3) k. (-5) (-3) (-2)
d. 3 (1 - 4) l. - 2 (-4 - 2)
e. - x (-y - 6) m. (-x) (-y) (2 - 3z)
f. (-2x) (-3) (-y - 4) n. 4x (x + y) - x2
g. x [x (2 - 5) - 2(1 - 2x)] o. 4 [x (2 - 5) - 2 (1 - 2x)]
h. x-1 (2x - 1) p. (-3x)-1 (6 + 2x)
2) Evalúe cada una de las expresiones siguientes. Escriba la respuesta en la forma más
simple.
2 5 12 15 20 3 4 4
a. + g. ⋅ ÷ m. + +
3 3 25 7 7 4 7 21
7 5 3 x 2 xy 14 x 25 y
b. − − 4 xy ÷ y ⋅ 9
h. n. ⋅
8 8 15 y 24
307](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-315-320.jpg)











![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
1+ a2 − 1− a2
4) Racionalizar y simplificar
1+ a2 + 1− a2
1 − 4ab(a + b) −2 1 + (a + x) −1 1 − (a 2 + x 2 )
5) (a 2 + 2ab + b 2 ) 6) 1 −
a2 − b2 1 − (a + x) −1 2ax
2 m −1
3m 9 * 32m 3m
7)
9 3 −m
8) [8
3 −2 n
(3 * 3 2 n + 9 n ) ]
1/ n
−2
2 n+3 − 2 n + 7 1 x −1 / 2 1 y −1 / 2
9) n +1 10)
− +1
2 − 2n + 1 2 y
2 x
1
11) 2x -
x − (4 / x)
1+ x 1− x −2 1
12) + * x −1 −
1+ x − 1− x 1 − x 2 + x − 1 x
x +1
1+
n+2+ n −4 2
n+2− n −42
x −1
13) + 14)
n+2− n −4 2
n + 2 + n2 − 4 1 1
−
x −1 x +1
x 2 + xy − xz x z+x
15) ÷ 2
⋅
( x + y) − z ( x + z ) − y ( x − y) 2 − z 2
2 2 2
2 1 1 a+ x a− x
16) − − ÷ −
x a+ x x−a a− x a+ x
319](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-327-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
a2 + b2 b2
a−b+ b+
a+b ⋅ a ⋅ 1 a a2 b
17) 18) − b 2 −1 +
a − 2b
2 2
a−b 2a − b b2 b a2
a+b+ 1+ 1− 2 −1
b−a b a b2
x
1+
x 2
x2 −1 a −1 + b −1 b −2 + a −2
19) 2x + x 2 − 11 + 2
−
20) −1 ÷ −2
−1 −2
+ ( a −3 + b −3 ) 0
x −1 x + x2 −1 a −b b −a
x − 3y 4y2 − x2 3 n + 3 − 3 n + 26
21) ⋅ 2 22)
x 3 − 27 y 3 x − 3 xy − 10 y 2 3n+ 2 − 3n + 8
6 ⋅ 3 2 n + 2 ⋅ 9 n +1 x + x2 −1 x − x2 −1
23) 24) −
9 3 (27 2 / 3 ) n x − x2 −1 x + x2 −1
1 1+ a
25) 26)
m − m2 − 4 m + m2 − 4 a − 1− a
⋅
2m 2m
8 x y+y x x+ y
27) 28) 29)
3 a −2 b y x−x y x− y − x
2 3 ( x − x −1 )( y − y −1 ) x 2 + y 2 − ( x −2 + y −2 )
30) 31) +
3 3 −1 xy + ( xy ) −1 x 2 y 2 − ( xy ) − 2
32) [(a-1 – 1)-1 + 1]-1 – [(a-1 + 1)-1 – 1]-1
[(4 ]
−1
a −1 + b −1 b −2 + a −2
)
1/ 2n
33) −1 −1
÷ −2 34) 3n
+ 8 ⋅ 8 2 n ⋅ 3 27 −2 n
a −b b − a −2
320](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-328-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
7) I = Io – bi i=? 8) y = ∝ (A – bi) i=?
9) M = ky – hi i=? 10) y = Co + cy + Io + bi + Go y=?
EJERCICIOS RESUELTOS
Vamos a simplificar ahora algunas expresiones donde utilizaremos las propiedades vistas
anteriormente.
2ax 1 − (a 2 + x 2 ) 1
1) 1 −
1 − (a + x) −1 2ax a+x
Cambiemos el exponente negativo a positivo y sumemos fraccionarios
2ax 1 1 − a 2 − x 2 ) 1 2ax 2ax − (1 − a 2 − x 2 ) 1
= − =
1 1
2ax
a+x a + x −1
2ax
a+x
1−
a+x a+x
Apliquemos ley de la oreja, destruyamos paréntesis y eliminemos términos semejantes
=
2ax(a + x) 2ax − 1 + a 2 + x 2 ) 1
a + x −1
=
1
[ ]
a 2 + 2ax + x 2 − 1
2ax a+x a + x −1
Factoricemos el trinomio cuadrado perfecto y además la diferencia de cuadrados para
eliminar términos semejantes
=
1
a + x −1
[
(a + x) 2 − 1 ] =
1
a + x −1
[(a + x − 1)(a + x + 1)] = a+x+1
322](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-330-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
1/ n
3 − 2 n 1 n
8 4 (3 * 3 + 9 )
2n
2) Bajemos la base 8 a 2 y la base 9 a 3; saquemos factor
común 32n.
1/ n 1/ n
1 1
= 3 (2 3 ) −2 n (3 * 3 2 n + 3 2 n ) = 3 2 −6 n ⋅ 3 2 n (3 + 1)
4 4
[2 ]
1/ n 1/ n
1 2n 1/ n 1 (3 2 n )1 / n
= 2 − 6 n / 3 ⋅ 3 2 n ⋅ 4 = −2 n
⋅3 = 2n ⋅ 32 n =
4 2 ( 2 2 n )1 / n
32 9
=
22 4
Para los siguientes ejercicios se debe tener en cuenta las siguientes propiedades :
−n n
a b
♦ =
b a
n
a an
♦ = n
b b
♦ am . an = am+ n
♦ (a.b)n = an . bn
n
a a
♦ n = n
b b
♦ n
a m = am/n
♦ (a ± b)2 = a2 ± 2ab + b2
♦ Restar y sumar fraccionarios
♦ Sumar o restar términos semejantes
♦ Factorizar un trinomio cuadrado perfecto.
323](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-331-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
1+ x 1+ x + 1− x 1+ x( 1+ x + 1− x)
(A) ⋅ =
1+ x − 1− x 1+ x + 1− x ( 1 + x )2 − ( 1 − x)2
(A)
1+ x)2 + 1+ x ⋅ 1− x 1 + x + (1 + x)(1 − x) 1+ x + 1− x2
= = =
1 + x − (1 − x) 1+ x −1+ x 2x
1− x 1 − x 2 − ( x − 1) (1 − x)[ 1 − x 2 − ( x − 1)]
(B) ⋅ =
1− x2 + x −1 1 − x 2 − ( x − 1) ( 1 − x 2 ) 2 − ( x − 1) 2
(1 − x)( 1 − x 2 − x + 1) (1 − x)( 1 − x 2 − x + 1) (1 − x)( 1 − x 2 − x + 1)
= = =
1 − x 2 − ( x 2 − 2 x + 1) 1 − x 2 − x 2 + 2x − 1 2x − 2x 2
(1 − x)( 1 − x 2 − x + 1) 1− x2 − x +1
= = (B)
2 x(1 − x) 2x
1 1 1 1− x2 1 1− x2 1
(C) x −2 − 1 − = 2
−1 − = − = −
x x x x2 x x2 x
1− x2 1 1 − x2 −1
= − = (C)
x x x
Reuniendo las partes A, B y C, tenemos :
1 + x + 1 − x 2 1 − x 2 − x + 1 1 − x 2 − 1
+ ⋅
2x 2x
x
A B C
325](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-333-320.jpg)








![DIEGO FERNANDO SATIZABAL GARCIA PROGRESIONES
1/ 9
5 1 1
r9 = → r9 = → r = → r = 1/2
128(20) 512 512
4) Los siguientes cinco números 2, 6, 18, 54, 162 forman una progresión geométrica
donde el primer término a1 = 2 y r = 3 . Por que r = 3 ?
Sabemos que a1 = 2 ; a2 = 6 ; a3 = 18 ; a4 = 54 ; a5 = 162
Si dividimos :
a2 6 a 3 18 a 4 54 a5 162
= =3 = =3 = =3 = =3
a1 2 a2 6 a 3 18 a4 54
Podemos observar que el cociente entre cualquier número y el anterior siempre es igual a 3.
La anterior progresión consta de cinco términos ; si sumamos estos términos el resultado
sería 242 veamos :
2 + 6 + 18 + 54 + 162 = 242
Y si tuviéramos la misma progresión pero con 15 términos por ejemplo, habrá alguna
expresión que me permita hallar la suma de una progresión geométrica ?
a1 (r n − 1)
R/ Sí . Cuál es ? Sn =
r −1
Esta expresión sirve para determinar la suma de una progresión geométrica, donde a1 es el
primer término, r es la razón de la progresión y n es el número de términos.
Nota : La suma de una progresión geométrica se denomina SERIE GEOMETRICA.
Si aplicamos la fórmula para el caso anterior tenemos : a1 = 2 n=5 y r=3
entonces :
2 [35 − 1] 2(243 − 1)
S5 = → S5 = → S5 = 242
3−1 2
Si la progresión hubiese tenido 15 términos, la suma daría :
2 [315 − 1] 2(14'348907 − 1)
S15 = → S5 =
3−1 2
S15 = 14’348906
334](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-342-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA PROGRESIONES
Ejercicio : Evaluemos si los siguientes términos constituyen una progresión geométrica.
1, 1+ i, (1+ i)2, (1+ i)3, (1+ i)4,. . . . . . . , (1 + i)n-2, (1 + i)n-1
a1 = 1, a2 = 1+ i, a3 = (1+ i)2, a4 = (1+ i)3, . . . . . . . , an-1 = (1 + i)n-2, an = (1 + i)n-1
Cual es la razón ? veamos :
a2 1+ i a3 (1 + i ) 2
= = 1+i = = 1+i
a1 1 a2 (1 + i ) 1
a4 (1 + i ) 3 an (1 + i ) n −1
= = 1+i..... = = 1+i
a3 (1 + i ) 2 a n−1 (1 + i ) n − 2
En conclusión la razón r = 1 + i y a1 = 1
Cuantos términos tiene la progresión ? R/ La progresión tiene n términos.
Si empleamos la formula, cuál sería la suma ?
1.[(1 + i ) n − 1] (1 + i ) n − 1
R/ Sn = → Sn =
(1 + i ) − 1 i
Ejercicios : Para cada caso verificar si los términos dados conforman una progresión
geométrica y hallar la suma de los primeros n términos, dado n.
1) 1, 2, 4, 8, 16, 32, . . . . n = 20
2) 1.2, 1.8, 2.9, 4.05, 6.075, 9.1125, . . . . . n = 25
3) 3/2, 3/4, 3/8, 3/16, 3/32, 3/64, . . . . . n = 10
4) 5/3, 5/9, 5/27, 5/81, . . . . . n = 12
5) 2, 3.6, 6.48, 11.664, 20.9952, . . . . . n = 30
6) 1, 1+ i, (1+ i)2, (1+ i)3, (1+ i)4, . . . . . n = 25
7) encontrar el octavo término de la siguiente progresión geométrica :
-1/5, 1/15, -1/45, 1/135,. . . . .
8) Hallar el primer término de una progresión geométrica cuya razón es ½ y el noveno
término es -1/8 R/ a1 = - 32
9) Hallar la razón común de una progresión geométrica si el primer término es - 81 y el
séptimo término es -64/9 R/ 2/3
335](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-343-320.jpg)









![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
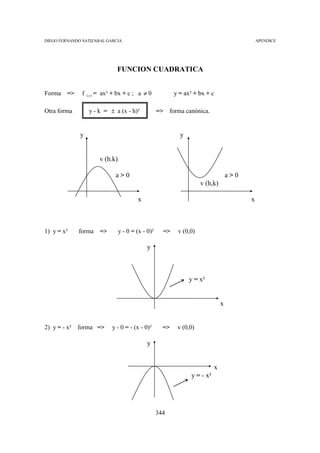
3) y = - x² + 4 forma => y - 4 = - (x - 0)² => v (0,4) Abre hacia abajo
si y = 0 => x=?
0 = - x² + 4 => x² = 4 => x = ±2
Dominio = (- ∞ , + ∞ ) Rango = (- ∞ ,4]
y
v (0,4)
-2 2
x
4) y - 5 = - 2 (x - 2)² => v (2,5)
Interceptos: Si x = 0 => y - 5 = - 2 (- 2)² => y-5=-8 y=-3
si y = 0 => 0 - 5 = - 2 (x - 2)² => - 5/- 2 = (x - 2)²
(x - 2)² = 2.5 => x-2 = ± 2.5
x - 2 = ± 1.58 => x 1 = 1.58 + 2 x 1 = 3.58
x 2 = - 1.58 + 2 x 2 = 0.42
Dominio = (- ∞ , + ∞ ) Rango = (- ∞ ,5]
y
v (2,5)
0.42 3.58
x
-3
345](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-353-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA APENDICE
5) y = - 2x² + 8x - 3 => y + 3 = - 2x² + 8x
y + 3 = - 2 (x² - 4x) => y + 3 = - 2 (x² - 4x + 4 - 4)
y + 3 = - 2 [(x - 2)² - 4] => y + 3 = - 2 (x - 2)² + 8
y + 3 - 8 = - 2 (x - 2)² y - 5 = - 2 (x - 2)² Es la misma del punto No.4
Taller :
Graficar las siguientes funciones cuadráticas :
1) y = - (x - 3)² 5) y = x² - 6x + 14
2) y - 8 = -1/2 (x - 3)² 6) y = - x² + 4x + 3
3) y + 3 = 3 (x + 4)² 7) y = - 2x² + 20x - 42
4) y - 6 = - 1/3 x² 8) 3y + x² - 12x + 24 = 0
VALOR ABSOLUTO
x si x≥0 |8| = 8
|x|
-x si x<0 |-5| = 5
Tarea : Averiguar las propiedades del valor absoluto.
346](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-354-320.jpg)















![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
EJERCICIOS PROPUESTOS
I. Resuelva las ecuaciones siguientes :
1. 1+x=3-x 2. 2x - 5 = - 15 - 3x
3. 4(x - 3) = 8 - x 4. 2x - 5(1 - 3x) = 1 - 3(1 - 2x)
5. 3 - 2(1 - x) = 5 + 7(x - 3) 6. 6y - 5(1 + 2y) = 3 + 2(1 - y)
7. 3z - 2 + 4(1 - z) = 5(1 - 2z) - 12 8. 5[1 - 2(2z - 1)] = - 3(3z - 1) + 1
9. 1 - 2[4 - 3(x + 1)] = 4(x - 5) - 1
10. 3[2x + 1 - 2(2x - 1)] + 4 = 2[1 + 2(3 - x)]
3x + 7 1 + x 2x − 7 3x − 2
11. = 12. = 5−
2 3 3 4
5y − 6 2− y
13. = y− 14. 1/3 (2y + 1) + ½ y = 2/5 (1 - 2y) - 4
2 3
1 1 2z 1 3x − 5 4 − 5 x
15. 1 + 4 (3z − 1) = 3 − 2 16. =
2 4 4
4x + 1 2 − 3x 4 − 3x 5 − 3x 3 − 2 x
17. −8 = − 18. − =
3 3 10 5 10
4 − 2x 4 + x 3 + 4x 4 − 2x 3 − 7x 4x + 1 2x + 4
19. − + = + 20. + = 3−
24 8 3 24 16 8 16
Respuestas :
1. x=1 7. z = - 1 13. y=2 19. x = - 4/5
2. x=-2 8. z = 1 14. y = 122/59 20. x = 13
3. x=4 9. x = - 0 15. z=3
4. x = 3/11 10. x = - 2 16. x = 9/8
5. x = 17/5 11. x = -19/7 17. x = 21
6. y=-5 12. x = 94/17 18. x = 9/5
II. Resuelva las siguientes ecuaciones por la fórmula cuadrática.
1. x² + 3x + 1 = 0 2. x² - 4x + 2 = 0 3. 2x² + 3x - 4 = 0
4. 3x² + 6x - 2 = 0 5. x² + x - 3 = 0 6. 4x² - 12x + 9 = 0
29](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-371-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
SISTEMA SIMULTANEO DE 2 ECUACIONES CON 2 INCOGNITAS
Un sistema simultáneo de 2 ecuaciones lineales con 2 incógnitas es de la siguiente forma :
a1 x + b1 y = c1 (1)
a2 x + b2 y= c2 (2)
Aquí tenemos 2 ecuaciones [ (1) y (2) ] con 2 incógnitas ( x e y).
Ejemplo :
y + 3x = 5 El objetivo de este sistema de ecuaciones es determinar los valores de x e
4y - 5x = 3 y que satisfagan las dos igualdades. Para este sistema los valores que
satisfacen las igualdades son x = 1 y y = 2. veamos :
Reemplazando tenemos :
2 + 3 (1) = 5 5=5 Ok !
4 (2) - 5 (1) = 3 3=3 Ok !
¿Como se determina esta solución x = 1 y y = 2 ?
Para hallar la solución existen algunos métodos algebraicos para resolver el sistema. Estos
son :
1) Sustitución
2) Igualación
3) Reducción
Analicemos estos tres métodos :
1) SUSTITUCION
Consiste en despejar de cualquiera de las dos ecuaciones una variable (ya sea x ó y) y
reemplazarla en la otra ecuación restante, para que se genere una sola ecuación con una
incógnita. Veamos :
(1) y + 3x = 5
(2) 4y - 5x = 3 Despejamos “ y” de (1) y la reemplazamos en (2).
Entonces de (1) y = 5 - 3x si reemplazamos en (2) quedaría 4(5 - 3x) - 5x = 3
31](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-373-320.jpg)



![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
La solución definitiva serán 2 parejas :
x 1 = 15/4 ó x2 =1
y 1 = - 7/2 y2 = 2
6) Resolver el siguiente sistema :
y- x+2 =2 (1)
y2 - 8x = 0 (2)
Podemos resolver este sistema por sustitución. Entonces despejando la variable y de (1) y
reemplazarlo en (2) obtenemos :
De (1) → y=2+ x+2
Reemplazando en (2)
(2 + x + 2 )2 – 8x = 0 → 4 + 4 x + 2 + ( x + 2 )2 - 8x = 0
4 + 4 x + 2 + x + 2 – 8x = 0 → 4 x + 2 = 7x – 6 [elevando al cuadrado]
(4 x + 2 )2 = (7x – 6)2 → 16(x + 2) = 49x2 - 84x + 36
16x + 32 = 49x2 - 84x + 36 → 49x2 - 100x + 4 = 0
2
Resolviendo obtenemos : x1 = 2 ; x2 =
49
Hallar y1 ∧ y2 y decir que pareja de estas es la solución.
35](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-377-320.jpg)





![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
Observamos entonces que para ese nivel de producción el ingreso es igual al costo, o dicho
en otras palabras, en ese nivel de producción estamos en ! EQUILIBRIO !.
Esto indica que cubrir gastos es equivalente a estar en equilibrio.
Hemos determinado 2 valores de equilibrio : (2000 , 10’000000)
2000 Es el punto de equilibrio en unidades.
10’000000 Es el punto de equilibrio en unidades monetarias ($).
Hasta ahora en términos generales hemos definido lo siguiente :
CT = CV + CF → CT = (c.v.u) x + CF
I = p.x
Con esta información podemos hacer la siguiente formulación :
U = I - C → U = px - [(c.v.u) x + CF]
U = px - (c.v.u) x - CF
U + CF = px - (c.v.u) x (sacando a x como factor común)
U + CF = x ( p - c.v.u )
U + CF
=x → Esta es la expresión para hallar el nivel de producción para cualquier utilidad
p − c. v. u
En este ejercicio sabemos que : CF = 4’000000 p = 5000 c.v.u = 3000
o sea que la expresión quedaría así :
U + 4'000000 U + 4'000000
x = → x =
5000 − 3000 2000
41](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-383-320.jpg)









![DIEGO FERNANDO SATIZABAL GARCIA ECUACIONES
17500 = 600x - 5x² ⇒ 5x² - 600x + 17500 = 0 (÷5)
x² - 120x + 3500 = 0 ⇒ a=1 b = - 120 c = 3500
− ( −120) ± ( −120) 2 − 4(1)(3500) 120 ± 400
x= ⇒ x=
2(1) 2
120 ± 20
x= ⇒ x1 = 70 ; x2 = 50
2
R/ Para que el ingreso sea de 17500 se deben producir y vender 50 ó 70 unidades.
[ I = p.x]
Si x = 70 ⇒ p = 600 - 5 (70) ⇒ p = 250 ⇒ I = 250 (70)
I = 17500
Si x = 50 ⇒ p = 600 - 5 (50) ⇒ p = 350 ⇒ I = 350 (50)
I = 17500
Nota : Podemos observar que en la medida en que la cantidad disminuye el precio aumenta
ó viceversa, (en la medida que el precio aumenta la cantidad disminuye).
b) p = ? ⇒ I = 18000 ⇒ Debo tener ingreso en término de p.
Para tener I(p) debo despejar a x en términos de p, veamos :
600 − p
p = 600 - 5x ⇒ 5x = 600 - p ⇒ x=
5
x = 120 - (1/5)p como I = px ⇒ I = p (120 - 1/5 p)
I(P) = 120p - 1/5 p²
Ahora reemplazo I = 18000
18000 = 120p - 1/5 p² ⇒ 1/5 p² - 120p + 18000 = 0
a = 1/5 = 0.2 b = - 120 c = 18000
51](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-393-320.jpg)







![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
EJERCICIOS RESUELTOS
Representar de las tres formas posibles las siguientes desigualdades.
a) x > 3 b) x ≤ 2/3 c) - 4 ≤ x < 5
R/
a) Gráficamente
0 3
Intervalo ⇒ S = ( 3 , +∞)
Comprensión ⇒ S = { x / x > 3}
b) Gráficamente
0 2/3
Intervalo ⇒ S = ( − ∞ , 2/3]
Comprensión ⇒ S = { x / x ≤ 23 }
c) Gráficamente
-4 0 5
Intervalo ⇒ S = [ -4 , 5 )
Comprensión ⇒ S = { x / −4 ≤ x < 5}
59](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-401-320.jpg)

![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
S = ( − ∞, - ½ ) ó S = {x / x < − 2}
1
-½ 0
3) Resolver :
5 - 3x ≥ 7 ⇒ - 3x ≥ 7 - 5
- 3x ≥ 2 (multiplicando por -1)
3x ≤ - 2 ⇒ x ≤ - 2/3
Nota : Siempre que una desigualdad se multiplique por -1 el sentido de esta cambia.
S = ( − ∞ , - 2/3 ] ó S = {x / x ≤ − 2}
3
- 2/3 0
4) Resolver :
2x − 5
≥2 ⇒ 2x - 5 ≥ 6 ⇒ 2x ≥ 11 ⇒ x ≥ 11/2
3
Nota : Dar la solución.
5) Resolver :
5 − 2x 4x − 7
< ⇒ 2 (5 - 2x) < 3 (4x - 7)
3 2
10 - 4x < 12x - 21 ⇒ - 4x - 12x < - 21 - 10
- 16x < - 31 (-1) ⇒ 16x > 31 ⇒ x > 31/16
Nota : Dar la solución.
61](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-403-320.jpg)
![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
2 + 3x 4 x − 5 2 − 3 x 5x
6) Resolver : − + ≤ −
12 3 4 3
− (2 + 3x ) + 4(4 x − 5) 3(2 − 3x ) − 20 x
≤ ⇒ - 2 - 3x + 16x - 20 ≤ 6 - 9x - 20x
12 12
13x - 22 ≤ - 29x + 6 ⇒ 13x + 29x ≤ 6 + 22 ⇒ 42x ≤ 28
x ≤ 28/42 ⇒ x ≤ 2/3
Nota : Dar la solución
EJERCICIOS PROPUESTOS
Resolver las siguientes desigualdades y dar la solución gráfica y mediante intervalo.
1) 4x - 2 > 6 R/ x > 2
2) 3x - 1 ≤ 8 R/ x ≤ 3
3x − 1
3) ≥4 R/ x ≥ 13/3
3
2 − 5x 4 x + 1
4) − ≥ R/ x ≥ 5/6
3 6
5) 3x - [2x - 3(6x + 1)] ≥ 2 - 5x R/ x ≥ - 1 /24
2( 3 − 5x 2 x − 1
6) − ≥ R/ x ≥ 21/34
3 4
2x − 1 3 − 2x 5 − 2 x 3x − 4
7) − ≥− + R/ x ≤ 19/9
15 3 5 3
2x + 3 3 − x 5 + 3x 5x
8) − + <− + R/ x > 13/28
18 9 9 3
62](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-404-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
Al final de cuentas gráficamente, tendríamos :
-5 3
De otra forma : S = ( - ∞, - 5 ] ∪ [ 3 , + ∞ ) ó S = { x / x ≤ −5} ∪ { x / x ≥ 3}
Nota : Debido a que la inecuación tiene el símbolo “ ≥ ” entonces tanto el - 5 como el
numero 3 son parte de la solución y se incluyen en esta. La inecuación anterior era de la
forma a.b ≥ 0 .
De que otra forma debe estar la inecuación para resolverla por el método anterior ?
R/ Para resolver por el método anterior se debe tener la inecuación de alguna de las formas
que a continuación se describe :
a a
1) ab ≥ 0 ó ab > 0 3) ≥0 ó >0
b b
a a
2) ab ≤ 0 ó ab < 0 4) ≤0 ó <0
b b
Cada una de estas formas podría extenderse a más factores ; por ejemplo :
1) abc ≥ 0 ó abcd. . . . z ≥ 0
abc abc
2) ≥0 ó <0
de de
Nota :
Se puede trabajar con cualquier número de factores, pero teniendo en cuanta que todos estos
se deben estar multiplicando entre sí.
65](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-407-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
( 9)(2) 9
iv) Si x = 3 ⇒ = − < 0 ! No sirve !
( −2)(5) 5
(13)(6) 78
v) Si x = 7 ⇒ = > 0 ! Sirve !
(2)(9) 18
-6 -2 1 5
S = ( - ∞, - 6 ] ∪ ( - 2 , 1 ] ∪ ( 5 , + ∞ )
Nota : Podemos observar que la desigualdad tiene el símbolo ≥ y sin embargo - 2 y 5 no
se incluye en la solución debido a que estos valores hacen que el denominador sea igual a
cero.
− 2( x − 3) 2
4) Resolver : ≥0
x ( x + 2)
Recordemos que ( x - 3 )2 = ( x - 3 ) ( x - 3 ) , si igualo cada uno de estos factores a cero,
el resultado será el mismo ( x = 3), por tanto se escogerá un solo factor de estos. Veamos :
x-3 =0 x=0 x+2 =0
x=3 x = -2 -2 0 3
− 2( −7) 2 − 2(49) 49
i) Si x = - 4 ⇒ = =− < 0 ! No sirve !
− 4 ( −2 ) 8 4
− 2( −4) 2 − 2(16)
ii) Si x = - 1 ⇒ = = 32 > 0 ! Sirve !
− 1(1) −1
− 2( −1) 2 − 2(1) 1
iii) Si x = 2 ⇒ = =− < 0 ! No sirve !
2( 4) 8 4
68](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-410-320.jpg)


![DIEGO FERNANDO SATIZABAL GARCIA INECUACIONES
3 1
15) <4 16) ≥ 5
2x − 1 x
3 4 x 3 − 4x 2 + 4x
17) < 18) ≤0
x − 1 2x + 8 x −5
5x − 2 1 3 2x − 1
19) ≤ 20) ≥
x+3 2 8 x+2
Respuestas :
1. (- ∞ , -2] U [4 , + ∞ ) 11. [-8 , 3]
2. (- ∞ , -8) U (6 , + ∞ ) 12. [-6 , 0] U [3 , + ∞ )
3. (-1 , 3) 13. (-6 , 0) U (2 , 5)
4. [-5 , 1] 14. (- ∞ , -5) U (0 , 3]
5. [-4 , -2] U [5 , + ∞ ) 15. (- ∞ , 1/2) U (3/4 , + ∞ )
6. (- ∞ , -3] U [1 , 5] 16. (0 , 1/5]
7. (- ∞ , -3] U [0 , 5] 17. (- ∞ , -14] U (-4 , 1)
8. (-2 , 5) 18. [0 , 5)
9. [-3 , -1) U [5 , + ∞ ) 19. (-3 , 7/9]
10. [-2 , 3) 20. (-2 , 14/13]
71](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-413-320.jpg)








![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
CALCULO DE LA ECUACION DE LA LINEA RECTA
CONOCIDOS UN PUNTO P (X1, Y1) Y UNA PENDIENTE (m)
Supongamos que por un punto ya conocido P (x1, y1) pasa una línea recta cuya
pendiente (m) ya está dada. Esto es :
y
m : conocida
El puntoQ pertenece a la línea recta y tiene coordenadas
Q (x,y) Q (x, y). [cualquier punto que pertenezca a la línea recta
P (x1,y1) tiene coordenadas de la forma (x, y)].
x
Si calculamos la pendiente de la línea recta que pasa por P y Q, nos daría :
y − y1
m= → m (x - x1) = y - y1
x − x1
ó y - y1 = m (x - x1)
Esta es una expresión que sirve para calcular la ecuación de la línea recta dados un
punto P (x1 , y1 ) y una pendiente (m).
Esta fórmula es también denominada fórmula punto - pendiente
GRAFICA DE LA LINEA RECTA
Un segmento de recta lo podemos definir como la distancia mas corta entre 2 puntos.
Esto indica que para graficar una línea recta, lo podemos hacer únicamente ubicando
2 puntos en el plano cartesiano; estos 2 puntos pueden ser los interceptos con los
ejes. Para hallar estos interceptos se hace lo siguiente:
Intercepto con el eje y se hace x = 0 y se despeja y
Intercepto con el eje x se hace y = 0 y se despeja x
Ejercicio :
Hallar la ecuación de la recta que pasa por los puntos B (2,4) y E (8, 1) y graficarla.
1− 4 - 3 1
m= = → m = - → y - y1 = m (x - x 1 )
8−2 6 2
80](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-422-320.jpg)













![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
INTERPOLACION LINEAL
Revisando nuestras matemáticas básicas, si se tiene un segmento de recta AB donde
A(x1 , y1) y B(x2 , y2) como en el siguiente plano cartesiano :
y
A(x1 , y1) y1
Sabemos que la pendiente del segmento de
recta denotada por (m) la calculamos así :
y 2 − y1 y1 − y 2
m y2
= ó m=
B(x2 , y2) x 2 − x1 x1 − x 2
x1 x2 x
Lo anterior me dice que la pendiente se determina mediante la relación que existe entre la
diferencia de ordenadas y la diferencia de abscisas pero ¡Conservando el Orden!
Supongamos que se tiene el siguiente segmento de recta en el plano cartesiano :
i[%]
A(20.5259 , 3.42)
3.42
C(20.7353 , i)
i
3.28 B(20.9479 , 3.28)
20.5259 20.7353 20.9479 Factor
Aquí se trata de determinar el valor de i para que el factor sea 20.7353.
¿Como se determina ?
R/ Se utiliza lo que se denomina interpolación lineal.
¿De qué forma ?
94](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-436-320.jpg)




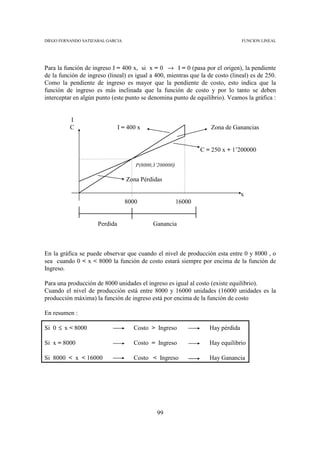









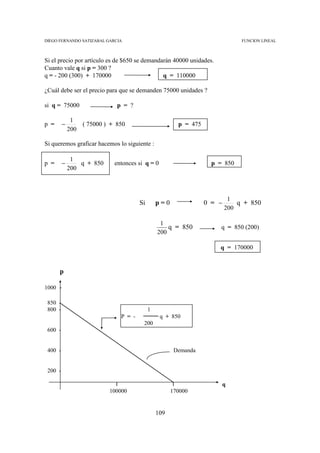






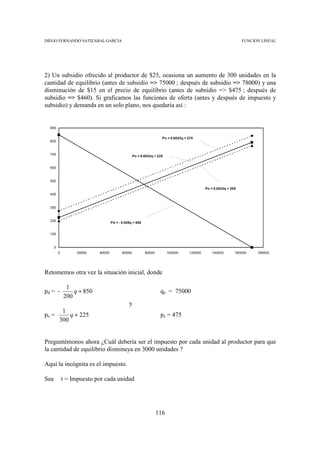




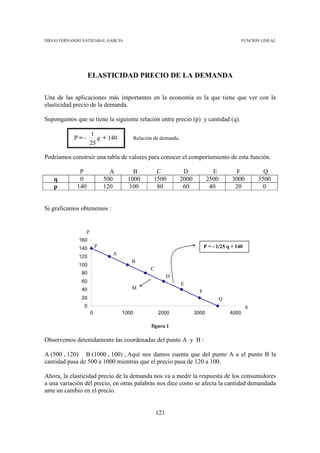








![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
C = Co + cYd → C = Co + c [ Y + TRo – tY]
C = Co + cY + cTRo – ctY → C = Co + cTRo + cY - ctY
Entonces : C = Co + cTRo + cY (1 – t)
C = Co + cTRo + c (1 – t)Y
Si llamamos c’ = c (1 – t) , donde c’ = Propensión marginal a consumir del ingreso total
Tendríamos :
C = Co + cTRo + c’Y C = f(Y)
Y = b + mx
Tengamos en cuenta que el intercepto con el eje de ordenadas es b = Co + CTRo y la
pendiente es m = c’ ó m = c (1 – t).
Con base en la siguiente ecuación c’ = c (1 – t) si analizamos detenidamente nos damos
cuenta que para que el valor de c’ aumente se requiere que c aumente ó t disminuya; y
viceversa, o sea, para que c’ disminuya se necesita que c disminuya ó que t aumente.
Resumen : ¿Cuando c’ ? → si c ó t
¿Cuando c’ ? → si c ó t
Gráficamente tenemos :
C = Co + cTRo + c’Y
C C
Co + CTRo Co + cTRo
Y Y
Figura 5 Figura 6
130](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-472-320.jpg)
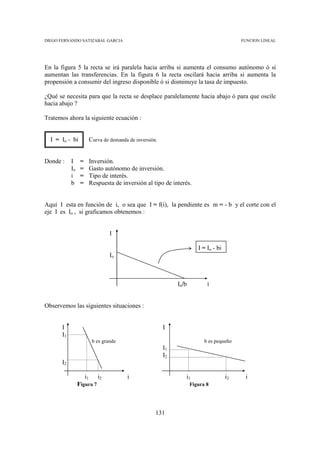














![DIEGO FERNANDO SATIZABAL GARCIA FUNCION LINEAL
h 1 h 1
i + bα i = α A - z → i( + bα ) = α A - z
k k k k
h + bkα 1
i
k =α A - kz
kα 1 M
iE = A− z Como z =
h + bkα h + bkα p
k α 1 M α
iE = A− Sea w =
h k h + bkα p k
1 + αb 1 + αb
h h
h 1 M
Entonces iE = wA − Este es el tipo de interés de equilibrio.
k h + bkα p
EJERCICIO RESUELTO
Dado : C = 90 + 0.65 yd L = 0.25y – 200i I = 150 – 100i
M
Go = 50 TRo = 150 t = 0.15 = 180
p
1) Hallar las ecuaciones de la curva IS y LM
2) Hallar las coordenadas del punto de intersección de las curvas IS y LM.
[o sea E(yE , iE)]
3) Hallar el nivel de producción y tipo de interés de equilibrio utilizando los
multiplicadores de política fiscal y monetaria.
Información :
Co = 90 Go = 50 c = 0.65 TRo = 150
k = 0.25 t = 0.15 h = 200 M /p = 180
Io = 150 b = 100
146](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-488-320.jpg)



















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION CUADRATICA
EJERCICIO RESUELTO
1) Por semana una compañía puede vender x unidades de su producto a un precio de p
dólares cada uno, en donde P = -0.5x + 1800. Si el costo de producción, para la
compañía es 600x + 420000 dólares por x unidades.
a. Graficar la función de ingreso I(x)
b. Graficar la función de utilidad U(x)
c. Cuántas unidades se deben producir para que el ingreso sea máximo ?
d. Cuántas unidades se deben producir para que la utilidad sea máxima ?
e. Para qué precio el ingreso será máximo ?
f. Para qué precio la utilidad será máxima ?
g. Cuál es el ingreso máximo ?
h. Cuál es la utilidad máxima ?
i. Hallar el costo en términos del precio.
j. Graficar utilidad en términos del precio.
K. Graficar en un solo plano cartesiano el ingreso en términos de p y costo en
términos de p y encontrar los puntos de intersección.
x = Cantidad [No. de unidades]
p = Precio de venta por unidad
p = - 0.5x + 1800
C(x) = 600x + 420000
Para graficar ingreso en términos de x debo tener I(x).
Recordemos que I = px
I = (- 0.5x + 1800) x
I(x) = - 0.5x² + 1800x donde a = - 0.5 b = 1800 c=0
Para hallar las coordenadas del vértice, hacemos :
b 1800
x= − => x= − => x = 1800
2a 2( −0.5)
166](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-508-320.jpg)








![DIEGO FERNANDO SATIZABAL GARCIA FUNCION CUADRATICA
El valor de p1 es el precio para que el ingreso sea máximo.
¿Como se determinó ?
R/ Para determinarlo debemos tener Ingreso en términos del precio [I(p)] y hallar
-b/2a.
O sea que si nos preguntan :
p=? para Imax debemos. →
tener
I(p) debemos. →
hallar
-b/2a
¿Como se determina el ingreso máximo ?
R/ Observemos que el ingreso máximo corresponde a la ordenada del vértice, o sea
b2
c-
4a
Si nos preguntaran :
Función de b2
Cuál es Imax = ? debemos. →
tener
debemos. →
hallar
c-
ingreso 4a
(cuadrática)
El análisis será idéntico para la figura 2 pero con la función de utilidad.
En el caso en que se tuvieran funciones de ingreso y utilidad en términos de q o sea :
I(q) y U(q) se haría de la misma forma.
Si la función es de costo (cuadrática) sería así:
C(x)
Cmin V(x1 , Cmin)
x1 x
175](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-517-320.jpg)





















![DIEGO FERNANDO SATIZABAL GARCIA FUNCION EXPONENCIAL Y LOGARITMICA
Recordemos que para hallar f(9) debo reemplazar x = 9
f(9) = 5e9k → f(9) = 5 (e3k)3
Como e3k = 2 → f(9) = 5 (2)3 → f(9) = 5 (8) → f(9) = 40
Ejercicio :
La ecuación de demanda para cierto artículo es :
p
−
500
q = 400000 e Donde q = cantidad, p = precio por unidad ($)
a) Cuantas unidades se demandarán si el precio por unidad es de $2000 ?
b) Cuál debe ser el precio por unidad para que se demanden 20000 unidades.
c) Determinar el ingreso para el caso a y b.
d) Escribir la ecuación de ingreso en términos de p [I(p)]
e) Calcular el ingreso si el precio es de $2000
f) Escribir la ecuación de ingreso en términ](https://image.slidesharecdn.com/obsequiomatematicasbasicas1-120302164953-phpapp01/85/Obsequiomatematicasbasicas-1-539-320.jpg)