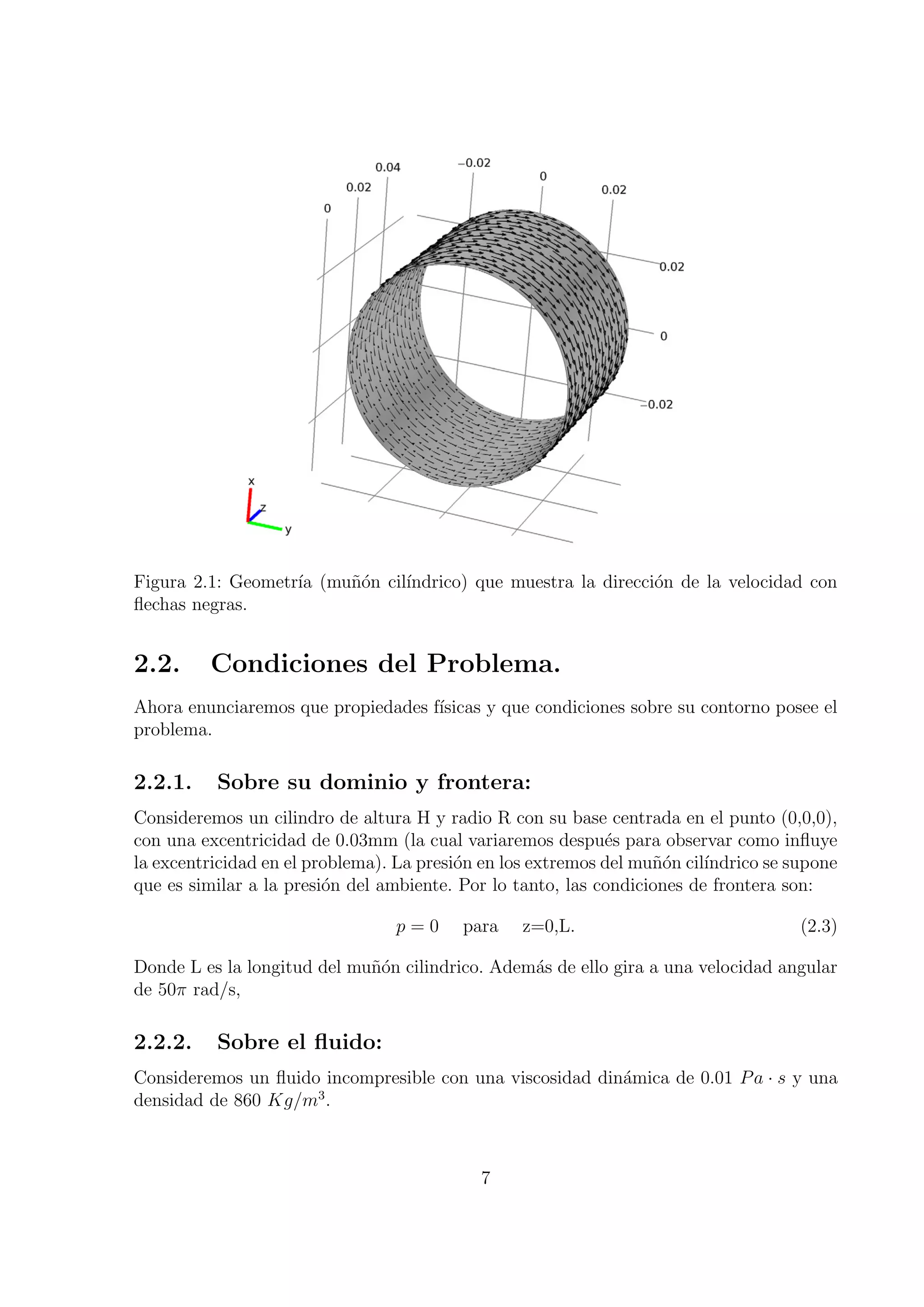
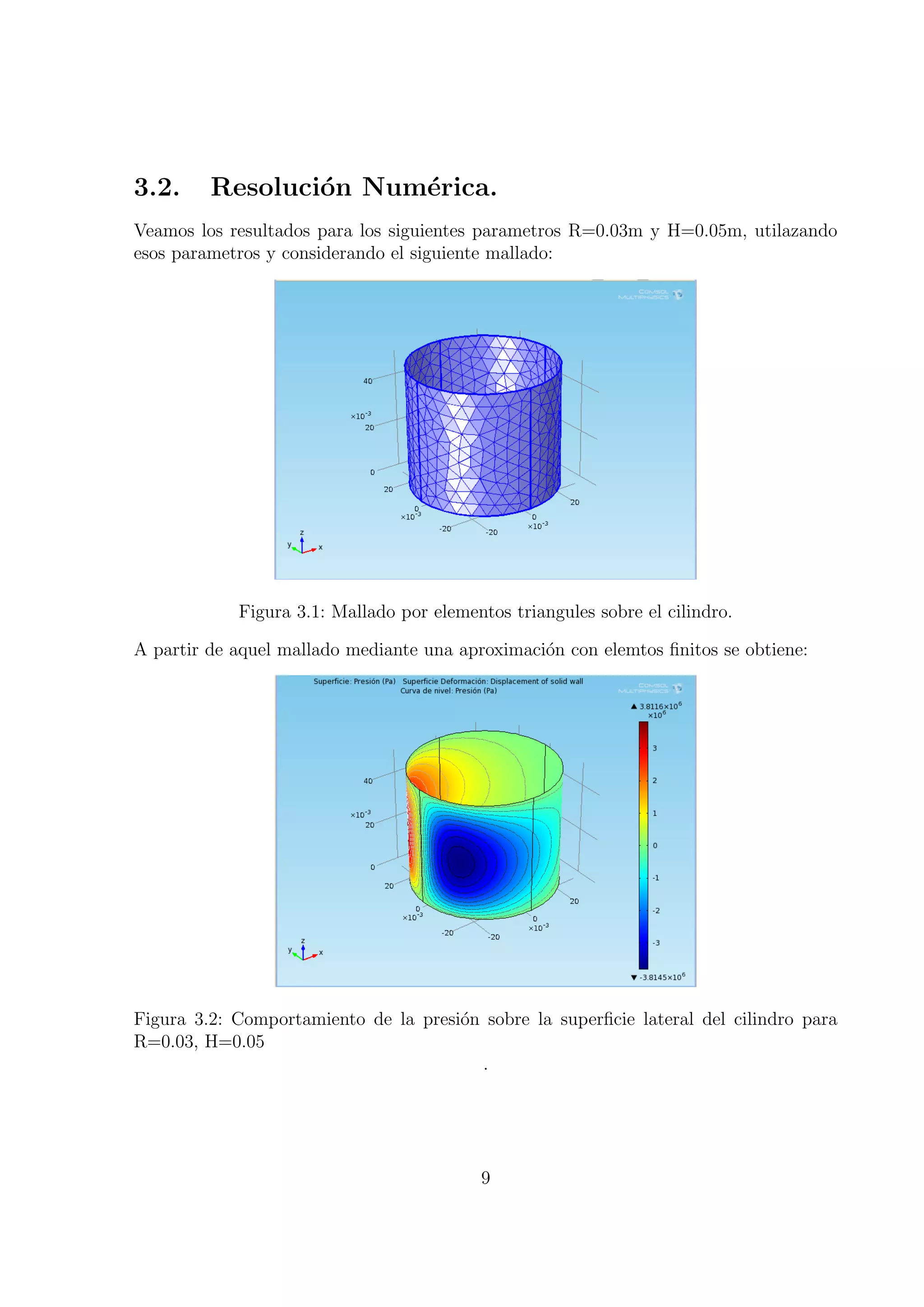
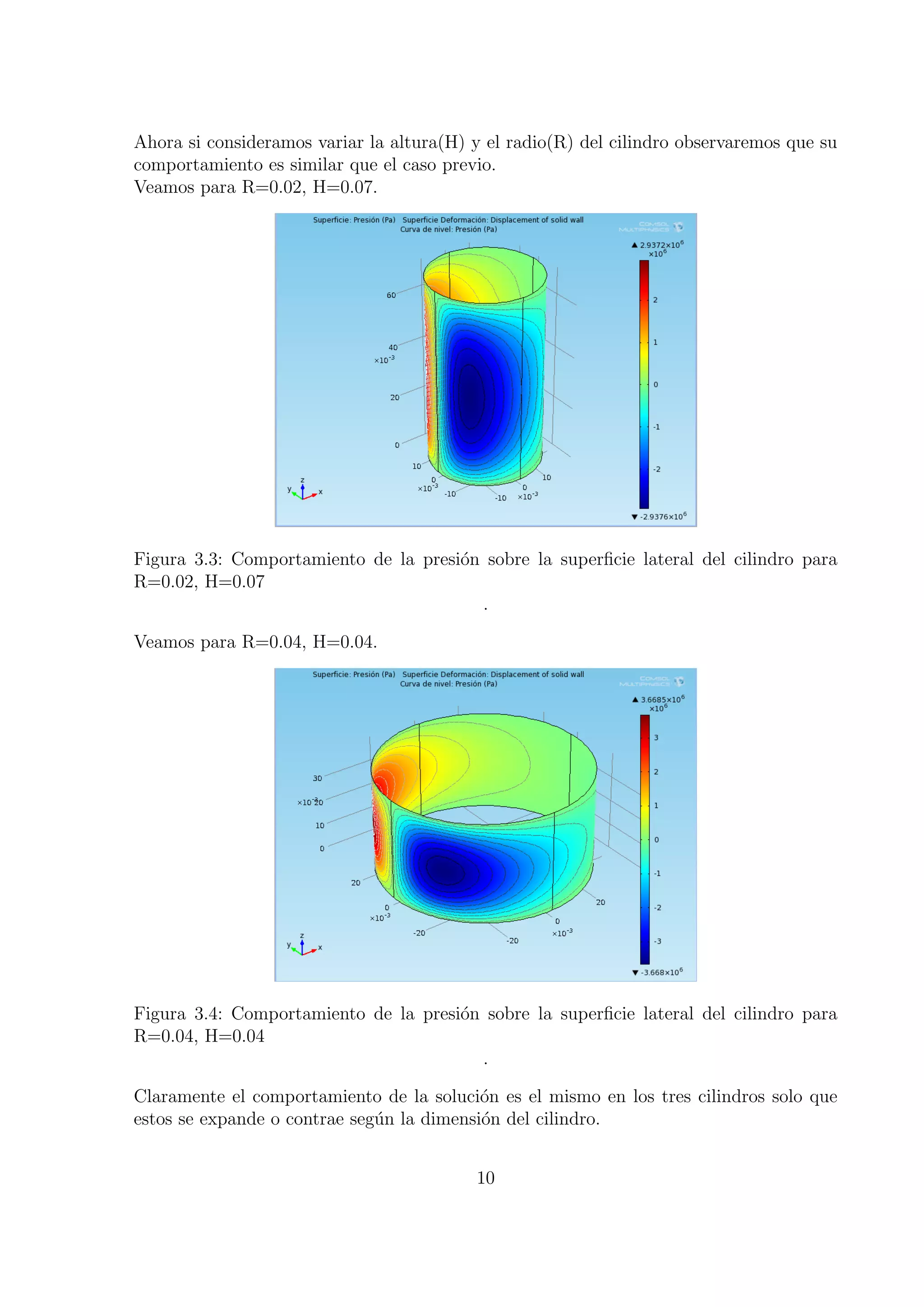
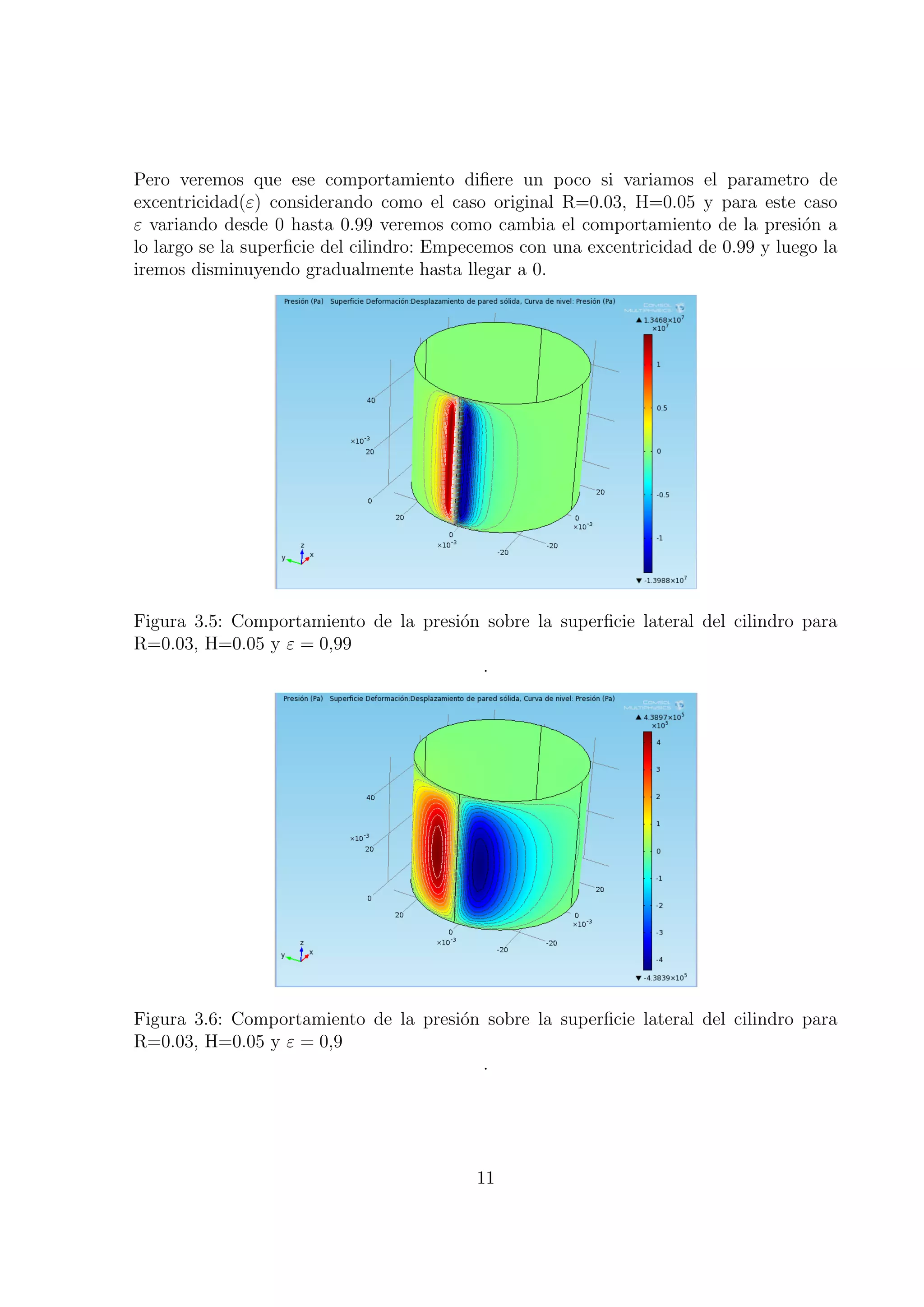
El documento describe la simulación numérica del problema de Brinkman utilizando el método de elementos finitos. Se considera un cojinete deslizante cilíndrico con lubricante incompresible e isoviscoso, y se modela el fenómeno de cavitación mediante la ecuación variacional de Reynolds. La resolución numérica del sistema de ecuaciones resultante constituye el principal aporte del trabajo.

1. UNIVERSIDAD NACIONAL DE INGENIERIA
Facultad de Ciencias
Escuela Profesional de Matem´tica
a
´
EXISTENCIA Y UNICIDAD DE SOLUCION DEL
PROBLEMA DE BRINKMAN.
´
SEMINARIO DE MATEMATICA PURA Y APLICADA II
Alumno: Soto Rivera, Joel Richard
C´digo: 20071155A
o Nota:
Asesor: Dra. Irla Mantilla N.
´
LIMA-PERU
2012

2. Resumen
La presente informe simula num´ricamente mediante el M´todo del Elemento Finito, las
e e
cargas radiales a las que puede someterse un cojinete deslizante sin que ocurra un contacto
entre sus componentes s´lidos. Asimismo, se considera el fen´meno de la cavitaci´n, el
o o o
cual se modela mediante la inecuaci´n variacional de Reynolds. Se considera un r´gimen
o e
estacionario, un lubricante incompresible e isoviscoso y dos grados de libertad en el des-
plazamiento del eje. Este ultimo resulta desconocido una vez que al sistema se le imponen
´
cargas, cuesti´n que manifiesta junto a la determinaci´n de las presiones en el lubricante.
o o
Su resoluci´n num´rica constituye el principal aporte. Se concluye, que para el problema
o e
tratado, la excentricidad es el principal factor que influye en el modelo f´ısico.
Palabras claves:
2010 Mathematics Subject Classification:35A15-37A01-35A02

3. ´
Indice general
1. Conceptos Preliminares. 4
1.1. Nociones de Lubricaci´n en cilindros. . . . . . . . . . . . . . . . . . . . . .
o 4
1.1.1. Excentricidad: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
1.1.2. Ecuaciones de Reynolds. . . . . . . . . . . . . . . . . . . . . . . . . 5
2. Definici´n del Modelo Matem´tico.
o a 6
2.1. Problema F´ısico. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.2. Condiciones del Problema. . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.1. Sobre su dominio y frontera: . . . . . . . . . . . . . . . . . . . . . . 7
2.2.2. Sobre el fluido: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3. Resoluci´n Num´rica.
o e 8
3.1. Formulaci´n Variacional. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
o 8
3.2. Resoluci´n Num´rica. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
o e 9
Referencias 16
1

4. ´
Indice de figuras
1. Componentes de un cojinete deslizante. . . . . . . . . . . . . . . . . . . . . 3
1.1. Posicionamiento relativo entre piezas mec´nicas con distintas excentricidades.
a 5
2.1. Geometr´ (mu˜on cil´
ıa n´ ındrico) que muestra la direcci´n de la velocidad con
o
flechas negras. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
3.1. Mallado por elementos triangules sobre el cilindro. . . . . . . . . . . . . . . 9
3.2. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.3. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.02, H=0.07 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.4. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.04, H=0.04 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
3.5. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,99 . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.6. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,9 . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3.7. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,8 . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3.8. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,6 . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
3.9. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,5 . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.10. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,3 . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
3.11. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.12. Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0 . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.13. Espesor de la pelicula del lubricante para R=0.03, H=0.05 y ε = 0,6 . . . . 15
2

5. Introducci´n
o
Desde la antig¨edad, el hombre se ha preocupado por la p´rdida de potencia en las
u e
m´quinas y el desgaste de las piezas en movimiento relativo. Tal es el caso que a´n, en
a u
nuestros d´ la investigaci´n de estos fen´menos tiene gran vigencia dada su complejidad
ıas, o o
multifactorial. La maquinaria moderna se proyecta para trabajar a velocidades y tensiones
cada vez mayores, lo cual obliga a una cuidadosa consideraci´n de los fen´menos que
o o
se presentan en las superficies con movimiento relativo,espec´ ıficamente en los nudos de
fricci´n. Un caso especial lo constituyen los cojinetes, como elementos de m´quinas cuya
o a
finalidad es servir de apoyo a los ´rboles(d´
a ıcese de una barra sujeta a torsi´n.) y ejes que
o
giran en el espacio, de manera que estos puedan rotar libremente y soportar as´ las cargas
ı
que act´an sobre ellos. El t´rmino cojinete deslizante hace referencia al conjunto formado
u e
por el eje, el casquillo y el lubricante, tal y como muestra la figura en un corte transversal
practicado a este tipo de elemento. De manera general, permiten el movimiento relativo
de los componentes s´lidos en una o dos direcciones con un m´
o ınimo de fricci´n. Adem´s,
o a
prev´n el movimiento en el sentido de la carga aplicada.
e
Figura 1: Componentes de un cojinete deslizante.
Journal Bearing: Es un dispositivo de antifricci´n en el que un eje cil´
o ındrico, al que se
llama mu˜on, se apoya en una pieza estacionaria, a la que se llama cojinete. se utilizan
n´
para llevar cargas radiales, por ejemplo, para soportar un eje giratorio. Un cojinete
simple consta de dos cilindros r´ ıgidos. El cilindro exterior (cojinete) envuelve el mu˜´n
no
interno giratoria (eje). Normalmente, la posici´n del centro del mu˜on es exc´ntrico con
o n´ e
el centro del rodamiento. Un lubricante llena el peque˜o espacio anular u holgura entre
n
el mu˜´n y el rodamiento. La cantidad de excentricidad de la revista est´ relacionada
no a
con la presi´n que se genera en el cojinete para equilibrar la carga radial.
o
3

6. Cap´
ıtulo 1
Conceptos Preliminares.
A continuaci´n presentamos las definiciones y conceptos f´
o ısicos usados a lo largo del
presente trabajo.
1.1. Nociones de Lubricaci´n en cilindros.
o
El desgaste es la mayor causa de p´rdida de materiales, por lo que cualquier reducci´n
e o
del mismo puede aportar grandes beneficios.
La fricci´n o rozamiento es una de las principales causas de disipaci´n de energ´ por lo
o o ıa,
que su control puede traducirse en un importante ahorro energ´tico.
e
La lubricaci´n es el modo m´s efectivo de reducir la fricci´n y controlar el desgaste.
o a o
El proposito de la lubricaci´n o engrase es el interponer una pel´
o ıcula de un material
f´cilmente cizallable, de modo que el deslizamiento se realice en su seno, entre movimiento
a
de m´quinas con movimiento relativo y cargados.
a
1.1.1. Excentricidad:
La excentricidad se define como la no coincidencia entre el eje de rotaci´n y el eje de
o
simetr´ La excentricidad puede tener lugar en diferentes tipos de elementos mec´nicos,
ıa. a
como son las poleas, las ruedas dentadas y en el posicionamiento relativo entre dos piezas
conc´ntricas, caso del rotor y el est´tor de un motor.
e a
4

7. Figura 1.1: Posicionamiento relativo entre piezas mec´nicas con distintas excentricidades.
a
1.1.2. Ecuaciones de Reynolds.
Las variaciones de la velocidad pueden concebirse como las desviaciones de la velocidad
con respecto a su valor medio temporal; de tal manera que las variaciones de la veloci-
dad se vean como una variable aleatoria de media nula. En tanto la presi´n, tambi´n,
o e
puede descomponerse en una forma similar, ecuaci´n (1.1). Esta variable aleatoria es es-
o
tacionaria, en amplio sentido, porque su media o esperanza matem´tica es constante,
a
independiente de su par´metro ´
a ındice, el tiempo; y la funci´on de correlaci´n depende
o o
s´lo de las variaciones de este par´metro,
o a
∂vi = vi − vi , ∂pi = pi − pi . (1.1)
Por tanto, cuando la velocidad y la presi´n se descomponen en la media m´s las desvia-
o a
ciones, para luego expandir la ecuaci´n de Navier-Stokes, y tamizarla con el promedio
o
temporal sobre la base de la hip´tesis erg´dica, entonces se obtienen las ecuaciones de
o o
Reynolds, ( )
∂ ∂ ∂ ∂2 ∂
ρ vi + ⟨vi vj ⟩ = − p + ρν 2 vi − ρ ⟨∂vi ∂vj ⟩. (1.2)
∂t ∂xj ∂xj ∂xj ∂xj
En la construcci´n del modelo se supone que la velocidad angular es constante, se des-
o
precian los efectos de la tensi´n supercial y se asume que el aire se comporta como un
o
gas perfecto, en el sentido de que la densidad es proporcional a la presi´n. Se considera
o
que la anchura de la capa del fluido es muy peque˜a comparada con las otras dimensio-
n
nes. Adem´s, se desprecian las fuerzas inerciales comparadas con las fuerzas debidas a la
a
viscosidad.
5

8. Cap´
ıtulo 2
Definici´n del Modelo Matem´tico.
o a
2.1. Problema F´
ısico.
La presi´n en el lubricante (SAE 10 a 70◦ C.) se rige por la ecuaci´n de Reynolds.
o o
Para un fluido incompresible con condici´n de ausencia de deslizamiento, la ecuaci´n de
o o
Reynolds estacionaria en el rango continuo est´ dada por:
a
∇T · −ρ (∇T b · vb − ∇T a · va ) = 0. (2.1)
En esta ecuaci´n, ρ es la densidad en Kg , h es el espesor de lubricante (m), η es la
o m3
viscosidad (P a · s), p es la presi´n (P a), a es la ubicaci´n (m) de la base del canal, va es la
o o
velocidad tangencial ( m ) de la base del canal, b es la ubicaci´n (m) de la pared s´lida, y
s
o o
m
vb es la velocidad tangencial ( s ) de la pared s´lida. Aqu´ el mu˜on giratorio se considera
o ı n
que es la pared s´lida. La figura siguiente muestra la pared y el mu˜on giratorio en el
o n
que se resuelve la ecuaci´n de Reynolds. Debido a que la presi´n es constante a trav´s del
o o e
espesor de la pel´ ıcula lubricante, COMSOL utiliza la proyecci´n tangencial del operador
o
gradiente. Notar que en este caso el t´rmino ρ (∇T b · vb − ∇T a · va ) es igual a cero de aqui
e
se simplifica la ecuaci´n (1.1) de la siguiente forma:
o
( )
−ρh3 ρh
∇T · ∇T p + (va + vb ) = 0. (2.2)
12η 2
El espesor de lubricante, h, se define como:
h = c(1 + ε cos θ)
Donde c ≡ RB − RJ es la diferencia entre el radio y el radio de rodamiento del mu˜´n, ε
no
es la excentricidad, y θ es la coordenada polar angular de un punto sobre el lubricante.
6

9. Figura 2.1: Geometr´ (mu˜on cil´
ıa n´ ındrico) que muestra la direcci´n de la velocidad con
o
flechas negras.
2.2. Condiciones del Problema.
Ahora enunciaremos que propiedades f´
ısicas y que condiciones sobre su contorno posee el
problema.
2.2.1. Sobre su dominio y frontera:
Consideremos un cilindro de altura H y radio R con su base centrada en el punto (0,0,0),
con una excentricidad de 0.03mm (la cual variaremos despu´s para observar como influye
e
la excentricidad en el problema). La presi´n en los extremos del mu˜on cil´
o n´ ındrico se supone
que es similar a la presi´n del ambiente. Por lo tanto, las condiciones de frontera son:
o
p=0 para z=0,L. (2.3)
Donde L es la longitud del mu˜´n cilindrico. Adem´s de ello gira a una velocidad angular
no a
de 50π rad/s,
2.2.2. Sobre el fluido:
Consideremos un fluido incompresible con una viscosidad din´mica de 0.01 P a · s y una
a
3
densidad de 860 Kg/m .
7

10. Cap´
ıtulo 3
Resoluci´n Num´rica.
o e
Para abordar la resoluci´n num´rica del problema, primeramente realizamos un algo-
o e
ritmo para su resoluci´n num´rica, que incluye una discretizaci´n mediante el m´todo de
o e o e
caracter´
ısticas combinado con elementos f´ ınitos, para la cual se debe hallar su formulaci´n
o
variacional para luego a partir de ella se aproxime su soluci´n mediante M.E.F.
o
3.1. Formulaci´n Variacional.
o
La formulaci´n variacional del denominado problema de lubricaci´n consiste en encon-
o o
trar p ∈ Va tal que:
∫ ∫ ∫
∂ ∂
(γh ∇p + h p∇p)∇φ + 6η
2 3
(ph)φ + 6η (ph)φ = 0, ∀φ ∈ V0 (3.1)
Ω Ω ∂x Ω ∂y
Donde Ω = (0, H) × (0, H), representa el dominio rectangular bidimensional de nuestro
problema() y los espacios y conjuntos funcionales son:
Va = {φ ∈ H 1 (Ω)/φ = pa en ∂Ω}.
V = {φ ∈ H 1 (Ω)/φ = 0 en ∂Ω}.
Bajo ciertas hip´tesis, se puede probar la existencia y unicidad de soluci´n de nuestro
o o
problema hidrodin´mico, as´ como la existencia de cotas de la misma[1].
a ı
El presente trabajo persigue como objetivo general desarrollar una aplicaci´n, basada en
o
el M´todo del Elemento Finito, para la simulaci´n num´rica de las cargas radiales a las
e o e
que puede someterse un cojinete deslizante sin que ocurra un contacto entre sus com-
ponentes s´lidos y considerando la posible ocurrenciade la cavitaci´n. El alcance de esta
o o
investigaci´n se limita a un r´gimen estacionario y se contemplan unicamente dos grados
o e ´
de libertad en la funci´n de holgura h. Como la variaci´n de la densidad con la presi´n en
o o o
los aceites m´s usuales es muy peque˜a, se supondr´ un lubricante incompresible (ρ=cte).
a n a
En adici´n, se asume un lubricante isoviscoso. Debido a lo fina que resulta la pel´
o ıcula de
aceite en estos dispositivos, dicha suposici´n puede hacerse sin una p´rdida considerable
o e
en la precisi´n de los resultados [2, p´g. 25]. Se consideran sin rugosidades las superficies
o a
s´lidas del cojinete deslizante as´ como un r´gimen de lubricaci´n hidrodin´mica.
o ı e o a
8

11. 3.2. Resoluci´n Num´rica.
o e
Veamos los resultados para los siguientes parametros R=0.03m y H=0.05m, utilazando
esos parametros y considerando el siguiente mallado:
Figura 3.1: Mallado por elementos triangules sobre el cilindro.
A partir de aquel mallado mediante una aproximaci´n con elemtos finitos se obtiene:
o
Figura 3.2: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05
.
9

12. Ahora si consideramos variar la altura(H) y el radio(R) del cilindro observaremos que su
comportamiento es similar que el caso previo.
Veamos para R=0.02, H=0.07.
Figura 3.3: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.02, H=0.07
.
Veamos para R=0.04, H=0.04.
Figura 3.4: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.04, H=0.04
.
Claramente el comportamiento de la soluci´n es el mismo en los tres cilindros solo que
o
estos se expande o contrae seg´n la dimensi´n del cilindro.
u o
10

13. Pero veremos que ese comportamiento difiere un poco si variamos el parametro de
excentricidad(ε) considerando como el caso original R=0.03, H=0.05 y para este caso
ε variando desde 0 hasta 0.99 veremos como cambia el comportamiento de la presi´n a o
lo largo se la superficie del cilindro: Empecemos con una excentricidad de 0.99 y luego la
iremos disminuyendo gradualmente hasta llegar a 0.
Figura 3.5: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,99
.
Figura 3.6: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,9
.
11

14. Figura 3.7: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,8
.
Figura 3.8: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,6
.
Observamos que mientras disminuye la los puntos donde se concentra la presi´n tienden
o
alejarse entre si proporcional a la excentricidad.
12

15. Figura 3.9: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,5
.
Figura 3.10: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,3
.
13

16. Figura 3.11: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0,1
.
Figura 3.12: Comportamiento de la presi´n sobre la superficie lateral del cilindro para
o
R=0.03, H=0.05 y ε = 0
.
Hay que tener en cuenta que para el caso ε = 0 se tiene un espesor de lubricante h
constante la cual origina soluciones periodicas a lo largo de la superficie.
14

17. Figura 3.13: Espesor de la pelicula del lubricante para R=0.03, H=0.05 y ε = 0,6
.
De manera similar se comportan los otros casos a partir de aqui podemos que la excen-
tricidad es el principal factor que influye en el comportamiento de la presi´n.
o
15

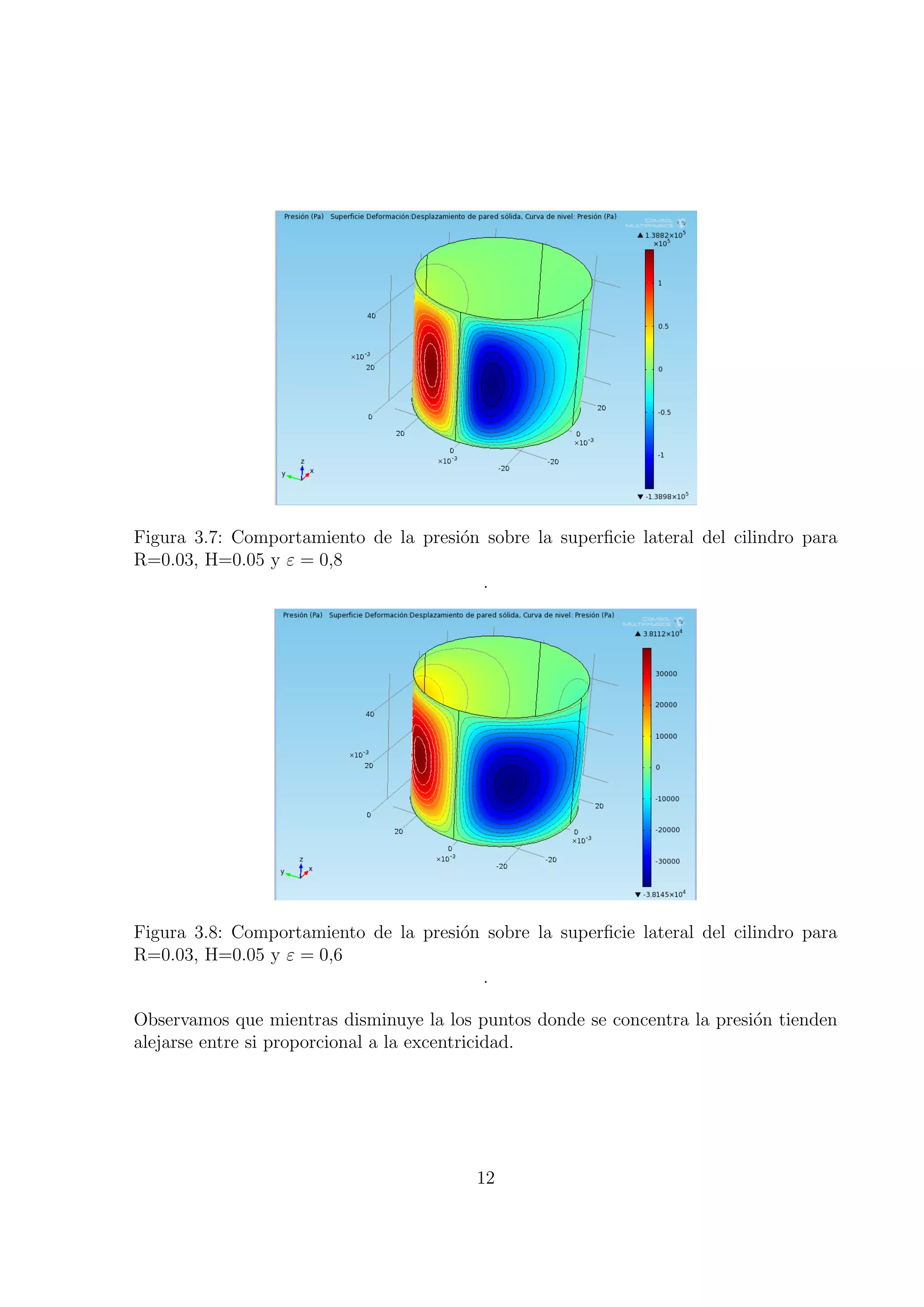
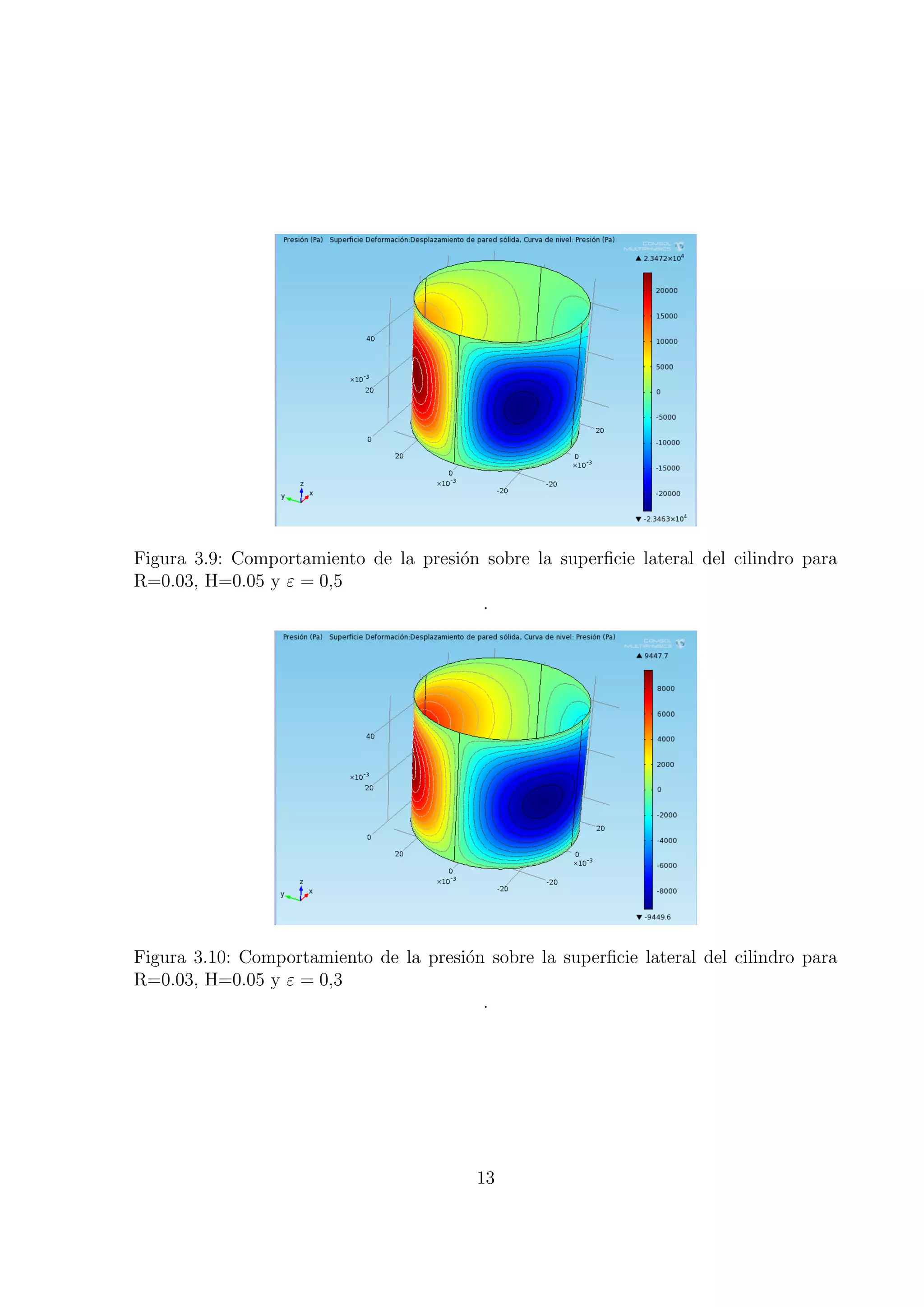
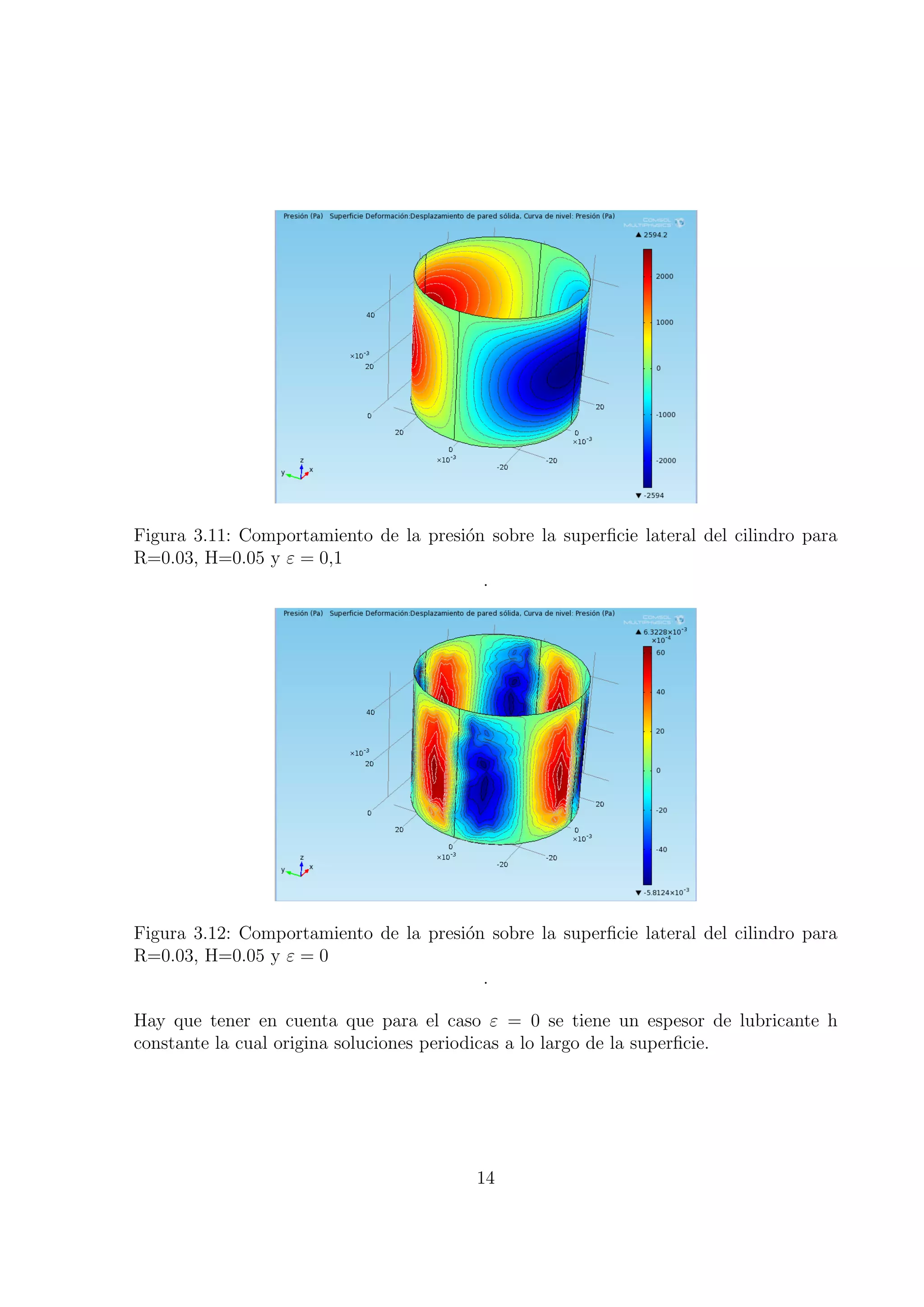
18. Bibliograf´
ıa
[1] Hass´n Lombera Rodr´
a ıguez Simulaci´n Num´rica de un Cojinete Deslizante
o e
Radial con Desplazamiento Desconocido. Inc.(2011)
[2] Hannukainen, Petri Non-linear journal bearing model for analysis of
superhar-monic vibrations of rotor systems. Tesis doctoral, University of
Technology, Lappeen-ranta, Finland, 2008.
[3] Dowson, D., Higginson, G. R Elasto-Hydrodynamic Lubrication. 1983. pp.
409-430 Printed in Great Britain
[4] Pinkus, O., Sternlicht, B., Theory of Hydrodynamic Lubrication . McGraw
Hill Book Company, 1961. pp. 41 -46-New York
[5] Irla Mantilla, Salom´ Gonz´les Simulaci´n num´rica de la cavitaci´n en co-
e a o e o
jinetes mediante elementos finitos y el algoritmo de Uzawa. UPGC- Espa˜a.
n
(2010)
16