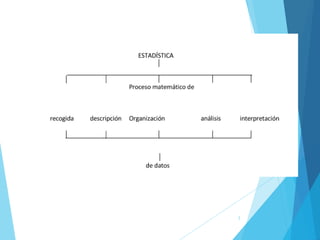
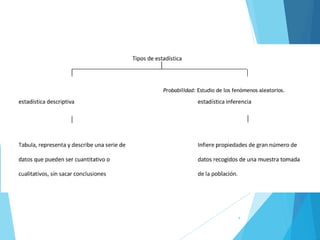
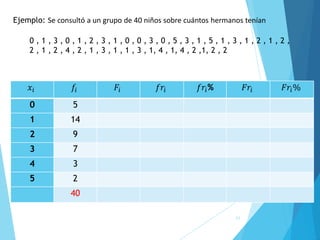
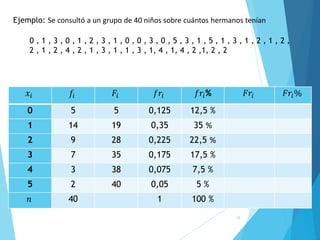
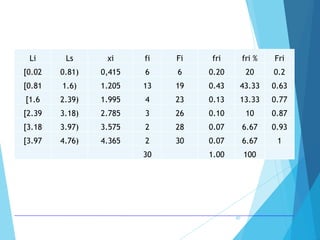
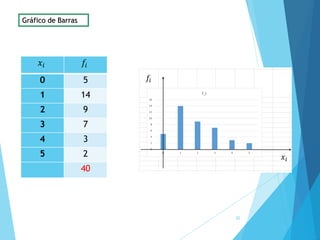
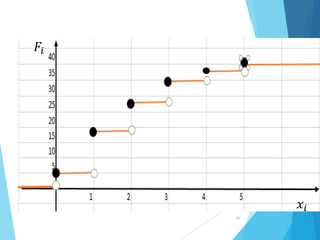
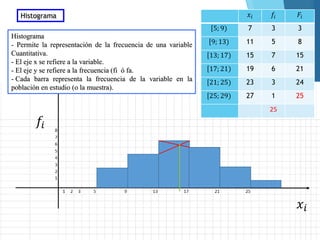
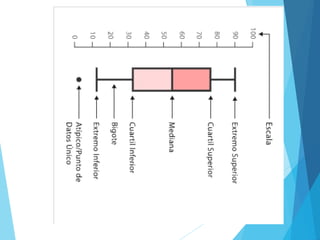
La estadística es la ciencia que se encarga de la recolección, análisis e interpretación de datos, aplicándose en diversas disciplinas como la sociología, economía y medicina. Se definen conceptos clave como población, muestra y variables, además de explicar las propiedades de las variables cualitativas y cuantitativas. Las medidas de tendencia central y dispersión son fundamentales para resumir y entender la información de una muestra o población.