1) El documento presenta un problema de ingeniería estructural que involucra el cálculo de esfuerzos en las barras de una estructura. 2) Se proporciona una figura con una estructura y se solicita determinar los esfuerzos en todas sus barras, indicando claramente si son de tracción o compresión. 3) También se dan datos como áreas de sección de las barras.




![. --. .~ _.'
- . _. . ..
1;
. . :.
,~~;.:~._,:'.~~:.."i~:{:"
,
.ti J~?..
"
;:
. ;'~ .
.
I I I I I l' I i.
~
I I U~J-1_iiJ-L
~I I I I ,1 I I
I i ¡ ! !..J..D-"':~-"': J-
I I 1I i ¡.~~ I
~
~_.L.¡ I t . "
--L1 :~~o:__:"":.~o~--L
o~ i..! iéV''-, ; ¡:ttl : ;-; !~ q+-i.~._:-"-~-1-. .:..
! : , !~--1 ~~ /L1...,1-.. !-~
LJ_LLLL~J_¡-+-J ;_o~_.;~ .1.~.~--
. i : ~ I I]1W~,:- .,.-Ti1 I . .: ..~ I
, ; i i : ¡ ~~~! -1 ~~ ~,~jJ-J=-i-~~.j~~~j1i:~1I1a~~i.t
T t ¡ í' ,,~¡ ;
~Li¡(o'! "'-.!
a' '1-1. . l
.
! .~.._~~~ :'
111 ; a.IÜ.C.Ui¡:-('.rt"".""~"''''1 "-
. ¡l'.!"#' ., ~
, ,..J 1': tí' "f.'{I-i_I_"", 1-.¡~'(u--i.#
z:g <'{"'</~ ,
; : t! ~ i
~. 'V," !T'-¡ .. ; t ~. i , :--, ! : . : ~ :::
--+++-+-r-=~~
¡ ! ¡ 1 T ¡l' C~j-i~;:;:~-~':.If~.i:='~~
-t-t+--+. : (!i) 1 ; : ; ~¡,:~-;H.i
~j-1f¿~"-~-'-
~~-- ,. - -;-' 1-
=q
L-..--"---"I--'/:-"Có, --..
I i I I i. ~ 1 I :-! i
~- 1''''';-~';'';i-~
~'-'''''; '-4-.""': -..---
11~~-~
; : .. ¡ :...,:_l--U-J-~j.~-+~~~!. .. .,_:._c_~.~-_.,--,
. ., 111.1 I ,.
I
I ~ I
1 ! ~ ! . 1
¡ ..
'."
I
. . : /u! . j ;
---i---Z.--i- ~._.l-.i---J~'; ..~ ~ -_o... .. _..~... ....-
I . I
,T
r i I ¡ ., I . , . '
. I
' ! ! : :.'
. '.,
.. 1:., I . '. "
.
.. ::-.~
1
"H (-,--""1
/
',-~"1'-'-':' --T ,-'--1-:' ~ . . ,
. - . . ..; ---: '-.-'
--Llt8--"--' v. I~-' -,~.~ ,- ;, J-~-¡ ' ' '---
~ i ;
.
;
: ~ . I i i
.
: : . .
. i . i : ,:
--~
,: .
'-¡-
Ó
-c;,:-':: ;," ,'T l'7'--:-:, :-"-;-:--: :-'
. :"
: ,. v~ 6 TI. I t . .'
-' .. .-.~ I. --,.¡, -- ~. :-.~_. . .
t ¡: I . '..:;: i .. i ~.
;
,
'~ ,
: . ':~- ¡J:-:-i-u' f'-¡"1/i-¡--:' .- ~ ~
.'-':--l
.--;-:o
-:-.~ o_-,u-:-- _'0'_" o
.
.
~J;.1i-..~ ¡ ~O..l.! ~ .." - -.. ,¡,.,,-"¡¡--~--'--.'--" .. ..- .. .. .-_.
; .
i : . ; I ~:':., t: t ! ! ! . . : :.. :
~ '
I
~""""~- ,
---, ~ ~.
, 0-- -.. oO-
, "..
"li/ ' I : . :
¡ . I ¡ . : , I
¡ o
,.!'II~'O O,"
:~I.I~"':'.
.
~ . . -. , -
.._..---
1 Ó
. I i ¡
: ; : i ,; : I I . ¡ . . : . : ! ,: .: ,.'
: '..-I !~_.! !--l l :~~~ J J~.-,- - ~1 ;--
j r; i ; ¡
m
;~. '-,&..-U ¡..;4tJ
i ; .J !~-1$..~~eP' ..1J~r' &r1~ ' ! -
i I;! ! I I I I ¡ : , !~
¡
-1 .
. j: j ¡ i I I j o 1 ; ¡ . . . :
'
?~ ¡ i-¡: 'O. ;;rI~T~~L~_.:~r~~r~~1:7. .L..L ---?A7Á2.J11i';~;:';.
I I I I I I I : ~ U.L.: : !-0i : 'i ! I i~_J~
Ir.: A: I 1- ()t.['/~(, '¡ !!:lit !~ ¡ I ! ; ! ! : : ¡ I , !_j .
.A..l.¡ I ~~ ..~ ,~---
I
-¡ I , 1
I
l ' I ,
I I ! i I I ! 1
.
"
1: i : I I :!
¡
I o.:
. l'
I
-..l--J I ~.
, . . '.-.1.--
t.:(>;' ¡"t!,o:J~ : I(D:': .'i
I ! '-,-: i: I I .
I I ;' ! i ! : ¡
I I I I! I I I : . i: ! ¡ i j ! I i.
r-11<1 -? 1~2.1'~I
: ¡ o,,
. I I! I I I : I
. : ! ~
i I ! ' !
I
,1 -.; ;-'::--,-,--, -. i--!-~-¡-oo!~_.-
~ I 01 iU ¡ i
. ~ :~ : :
! i : ~
: !! ,:
IFII'"" I f, J I .C'FITl ! : ; I
'. "
. i! 1; ;
I ¡!I liT"T"í,-lT¡I¡I' I
." i I I !¡I;
¡ :-
!: I 1,; I 1 ! I
'...,
1 . I I i ¡ : ¡: iL- "
, -'1..';..1 ' , ~b n;"~
:': ~ '
i ¡ ! , I :
;
I I l.; ; ! I I
lh~ Jj' Id ~_L' 1/ I,,~ ~ Fili"':~'-:~.
I ~: r i ¡ I i : '1 : '
íí t I ~
! .~. ¡, l. I I i!'
'IM ¿:p.. j ,,: i r,""" ,~ &,41~d4..ed:!~i..~i ;~.:,.~;tL"t
-
~ '¡
I
t':5~ .j~~ji~L; pl';f;6'_~.~~~~~~C~.~.a~~---i::Jilil.
1;;lj'¡!' : i
I 'iI ~31 "'°" ¡ I 1 Jj,-L '; IIIJ74.3",:!- D~iZa~~"¿!2...!)S.. .-
r~~i-f¡::6f--rl--h:{ ~¡I~~0.~-f'~~~~c.;;_~'I~ :~~:: - ~ .
I~~
-.;
, ;:-. ~ fo!t. .
}-1. - ~, ,e.? t..
,
~'1!
JJ l. 1 P;'G4I.~
..
.
I
~L
8
-I
f! .
,
.
:
¡
...;
;;
i-
ro.'
-.
i,
"](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-5-320.jpg)
![,
? dI;
ít,~ L.. ,4; z 1(.'Zl-
~<'"', N."ot' i . :-r--
. ,
,¿f¡ 4.ó ~. I/:¡f" I.J 1,;¡c3
SCo M' ,"D 11.1[' 1,(' D.;.oJ
,
~E 1.J' l[ -SI.zr D.f.!.J! -.t.";
~E ¡.r Ir ."jL1f -P.I!]! L¿D'
T
-M'p(
PROBLEMA
0"
Calcularl.'componente horizontal del corrimiento en el nudo'.
de 1. estructura representada en 1. figura.
,,-
D.tosl las áreas de las secciones de la. barras s. indican entre pa.án-
'tesis en l. figuraCcm2).
E.2.1xlO T/cm'l.
r~#)
&",
.
-.¡- f.f
'"
~$"'--t-w~-
(J)¿avE./Z2o~ at,~r .::::~ ~
,.,,,,-1 : ~o{. c.,
lO. c,(' 0.8
'1:~r
1zr t5t> '1.(
("'V¿:"""'~2"'1 ~6;[;o:;" C", t'uu tWr~ /foait...,rJ.I.. EIJ (i
!
{. 4_i
¿ .! II;Eá
f. /lb
" - -
l¡i - -",4 '~ - ,
J=J
-
~ '
0$
-l.l>.&(1'.r t".1(1 Dti.:
t1.<'/","-, H1 ". .,. ""' ..,,.,. ",": v."~ ~(VIr.
':./ <ID~ U-,'I.
.
-
~:.](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-6-320.jpg)




!["
t'
l¡
,,.
",.--
¡
]) r
.. . -
~:1::;:~~~~:';:[~~~AD
NACIONAL DE EDUCACION A DISTANCIA -t~f(dzjjIJL I
/~::>.ESCUElA TECHICÁ SUPERiOR DE iKBERiERüS iHüü5TRIAlES' 1..1,- 'Z.
;
;WPo,{: ~6
~ "
I(~
.ft;:~ r.> 4 -A.;.. ;:0
" l~-~~
~
. .-,- =0 -, f" ."
, .: , ":
r,.,
'*4 r "'>' ¡¡ -= - , !,-~8--¿J
i----...---
ZrHoo.;!l ,lIt. =Z . 14,. ~/? '
ff ' ~
I.t'~.s: :2
115'"
~/~
¡t"t>~e :
~
l~JGD
f/Fr.. ;;11
.
I --- f
,.~
If =
/¡
i ~:: 4vf i
t§= - 4tK ~= 3fF;¡ ~o ~
eL
¡{fve.. lJ .. ~ l'
¡> 1
t2z ,,,,? ~?"
o'
'..
'Z. 4~:v
,
..( ,'- .
,.,--,' '--'--' ".
.n' -.. .](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-11-320.jpg)









![~. .1/:.. A. UNIVERSIDAD NACIONAL DE EDUCACION A DISTANCIA .
~t>.
ESCUELA TECHICA. SUPERIOR DE m6EHIEROS.I~DUSTRIAlES .
. , '"S...Je ~_.
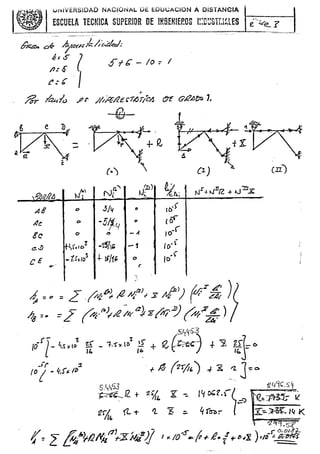
(1) ~H~ ~:> -"') /f¿~q~ /.. g .,.::) ~..~"
Z f"" "o
.,;> fl€ i .r =~ ~=~
.r - ¡¡ lIS
zJ; ~.. -;? 127) -:. I +
,r .;l=1...:L - 25'
- {'6
,.
J 11.
- -1(.
¡J 3 =..1 -, IJI..c: ~1'13
.l.t:.. ~.!"
COl -¿
F" =.. :i:) r<.r:; J : e rJlW ."...,
.r.
¿- r,., :.:>::;> kf ~ :- IIJ) ~7
J
n ""'.. ,r::I ., - ~
.t'<:€:.,r :: -r,ó)<../O
1/
'1
f{b ~ § ].(~ID= 4-..fK lO]
s-
.
?'
e](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-22-320.jpg)






![,-
J jp"c.. t-
fi;/ J
'Y
't ,,---"1 "-
., , (oí
..?~
. ¡P. A;¡'.i.r~ ,/ ~a "i<eDI'" -.~ fs, = .,. lo3T~.
:r..» k¡!/.! '1" ,¡ ~.:Ik ~he t!. d.;'o?C~A<" 4r .~Q,.
~
la. ~ k ~ l¡/~
e/ ~.uu~-6 c:vb C' ~ .J~"1 ~c.b..
a &¡
~
~ -:: K: 2>:: ~ 1< Ié
~
"yK'"
1..ov-O I
=
I 01
~
!
':'
I
1L6. ~
r,~/r)-']= Z[ifI (1-/0) e 1 tJ ~+ -z (¿~ 7 ID-.rr. fo
En J 0i ú1
".
-- ---...
V= ID.'
'2.n "
(
- --. -
H---- - - -](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-29-320.jpg)

![" ~~~~;~A-';~~;I~~ ';~~'~;~:~:~~;E~~~;~~ ~N~;S~~~~~;
.'
~ -.u - --_u_..----------.-----
J~t (
(i-=-~
I
J'",:r-;:(O~ (f -t~ = (/
.' ~~~~ R/)~~ .
I~ ~kIt7~/'b<-~"l~ O:ho.
/.
.
~~~. ~;fk~
7.'~
?/ev'7::/4A"J
'f'l'-
.."j,'..
"
.' ..~,.
C[:-bt(Ó (f'. .
.
~/í f.o r,,;r
)/Yr ~ ~-¡L {IV,
,
--
.
A . !JdOD ,6; .
'r~ .
tNiJ!
~
L , ~ / "
tJt¡¿ ~..:: I -") I'-'.4E -=-
lj
.
( Ca''lf'
/
M - IV¡¡E~ '] --1:' :) _:? (~Py,)
'}g - J "
4' f"
-4' /
(
/~ .f{1 J3J-
1JJ$b
. f
'1
. ..~
/¡Je~ :: NE,4 ::
j (' 0w.lf.~ /(¿fF 11lf~'i1.-:;y;;
.
9 / I ~I
.
AhD:: ~ír ::: 2 (~¡¡r)1
e ~~ t..2 :: i ~) I~~ ='
Vii (;7"{,C<.~
t¡ /.: .
tIii-
I¡ -, 11
ÁtEZ)-= ~l?~:- [h::rn~)
/t&--J~!- !L: ~L::-.l (&w/Y.)
. t/f:! /1!Jf{ :s
B.
:
e-)
, .
¡ /
fh- eA p?dÍ/ f{ :,
aJ;(,~:
F ¿ - ¿Al" IJ~ ~~;:F1¿ -fd
}/V--L:::2 ¡- (J)! -t S}Jt~::
€ I!CA. f ~/I '. u" -
~~1'{~~. (-3 >ID" )¡~) ~ f'5,1DS?, ID
,4
f
~
~
I¿-'" - F 10'
f :: -
o}
{O-,3
.
,
-=- -3,~04 T
:-_-;//1 4 6.~DGt~
?=11J?c ::(-3: 3S'~) ,
;t/ii
z.
l ¡f
E~
~
1'.""
~
,í J 3.. ID'¡VA
,_ l,.
~,
- /M
J'~ÓA-'¡
c.
/ IJ "(.,,{?
--r('l:> '/r..l../&)r.-( . 1
-, - --------.....
..
- ."" 0..;.-/ X. -.---](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-31-320.jpg)















![Q~::-. ..~ :uNi~E~g¡dl~'N'Ab;'o~~t Ó'~:E'~~bAC16N:~ ¡:m;TA.NCIf I ..." i-l.-
..- EscÚÚA.iÉ'CH-íC¡" SUPERIOR- 'DE iH6E~íEROS iHO'U'STRÚÚS. .tJ~~ ".,,'
f ;r
(: ¿ -t{.
¡(f¿.!"
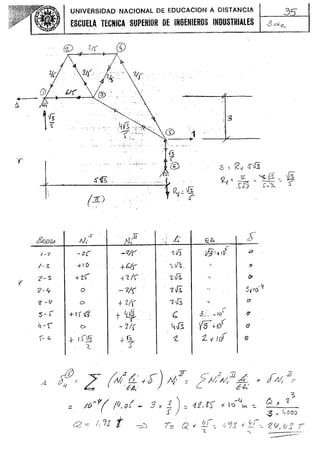
(~~ -/ Z Ni (2 oé IJt)¿ ::
'..
.
-¿ir N¿I.¡x 1./;:) ~..z-~~1¿ .¡ z4 (¿ Dl 4t),: ::
- F !¿{- ~.í):. .r.,l z(J)~q.f 2(o..)t~il-
Ir /}Vl)-
i
-,l >( Z z{- Z:{ )2.j-f 2 /2
J~ -f ~(o.r)~J7.¡. z(. z.nr-oO(/D-~fo=
IJW'b / C3 J . I.J
-= F~ 1S'.3
~8~:r~
~~~ x + !96 ¡= = vS""c (
-1 "
i
~;; -< /,IJl..¡. ;(. Ni.IL
)
' N¿:iIí..f.
) . ..L ¿ Al: (¿ ~ ~t)¿ ~
dz-' ¿
t ' . l6'~ (,.
:: X L
~
J1i:}If'''¡' + /06 F ::. l¡f"c
]
~k/~ at. JúL :
~
X = ¡,7rt1l ¡-
íí r ~ o,6'oS- T ....
~:
M-!"; r!i-: -r%-IJ;'-:;(lrbor(6)J.!.9{V{-?f)<;-/~ai:
-- .
1
~
~r ~ M
.
;::r
. .
¿ 1-["
::
.
/. en IL r =
~
¡;t¡I1"IO-lf M
.
J~" (JcoV
- - - - --- -- - ~--.'
.
--- ----](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-48-320.jpg)



![.s~.o".,
"".~.; '1.'."
f
.3-S01r! 3.~o /1
f
o.S"'o a-
{ 3.$01>'
f
3.S0f/
f;'''
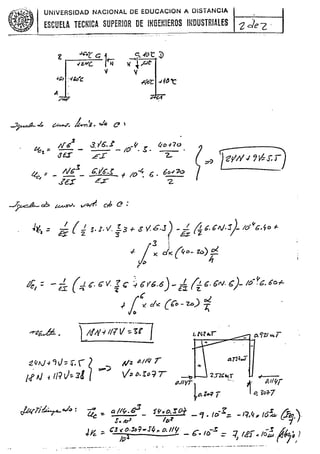
PROBLEMA
S1
'.-Calcular las lineas de influencia del e~fuerzo axil de las
- bar~"s _A13'_13.C ,AC. ,LB!)_~é!_J._~~s~Z:1.Iet:uI"aureprl:sentada_en..lIi_fi¡¡ur~_cuando un&-.-
carga unidad recorre el cordón superior.
..c e
~ ~
,
.g ~ 77ZZI
3,)0/'1 J./"o
"'"
.? ro ".. 3. r""", 5 ¡-OM
...-.....
- NAB'"
'- "-- i
I,
-.------L---- 1,11..-
~-........,
N"
.~B§
'G)' .oj" ; .
o.L/]
-'----"---.--
."~ : 1,: l
:
lf(~~
.
- I -"ff
-.
-'o
:11.
'. -- ~,
r~..." !
: i "
.
Í~
rf-
?r
o...¡
. :l
-=..!-.
;,,:..;
--"t.:'-](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-52-320.jpg)









![""'w.
."~:s .".
'.
- ~~
UNIVERSIDAD NACIONAL DE EDUCACION A DISTANCIA
ESCUElA TECNICA SUPERIOR, DE INGENIEROS INDUSTRIALES
{;'
--3
z; .J2a~~ .-el dor;h,<-.~~¡;/.w¡;(x{
c¡):2 E :
!J;:L~Q~ "¿_é~~II;~,_f;,~N-lí)II$=¿ E¿ (,12~~~ ~/)/)
. .
"
;
."
.." .:. --'''':,,;-( ,-- '-- _0.-" -. . .
..
-~'" 1~/t5:t¡
.
.//Z ":='&:'~
.
4-;]~-T
).
~
""
.
'
.
'
':;-'
.,,"
..~'
(', 'V,
"',
., I-¡;g"
o-o --
,
'. -.-' ,-- . - -
; .~~ ID-"~
11',- ;¡1?!~~~~-'f~/~
".'
-V
A
,/J/.¡ -¡ 1'7 I
)i,,/o /C. - - - IV-
-1 3¡!J ~
(2)
.
--
...
- ~
'C
4/ di:;f'¡{~:r d4 r;):"
1-)2 -
z~~c
R.. .'
i,
- ',' :::)
1'oC¡¡
,
1:eo ¡¡
'~> ~
":ÓDf)
f(°7/
.-. .- ~_.--
-----.-----------
~ ~~ el ckrz~t:.'lovW¡f~1~ E t#
1~ (7)/--'
I
P;2~( - ~;; o
~fF
,U/l- (oq
'" i('
"-~-.. . n_--' -- --. u" --_o
';
,
I ~/ ~ ~/ ,4x,,'1 ~ ".~',
.,~
¿(;¡ 8«¡{au.c6 ~¿s):
,
'
(A6:.
~
,,¿¡
;2 e P.(Ifrr l?- 4 ¿/
"'~ "" .d ~w.~
"
~ /,;/d:e.a..6. ~ ¿//~,8 ,E,
, ,
J/( !Ml?í
=-'d'
g@-r
C~
~ k c.{, "',,~ t<;....
;¿;c,'-.
'-
"-..'..,:...<.p...l"t-le..
<-',](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-62-320.jpg)




![.r.~;:~S;~I;AA~~~:~:~:~~~~~:;~:o;;;~~~I.~~-'.I!~I 1-
I ..~.
"'1 .' -- --., "'-"" I
I
I
.I
.--'- --'/5
e .
~
~
. -.
..".. -,. ,.
. -~--?' '-';-'-:"~
~ .~
0.'-
," 1 -. "'.
. .
.
- '.
.
. u :.."- -- ." ~-'
-,
. Á ."
/, . /
.-
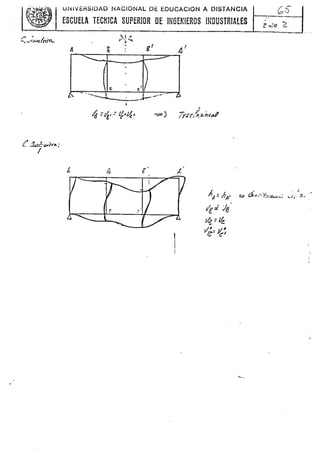
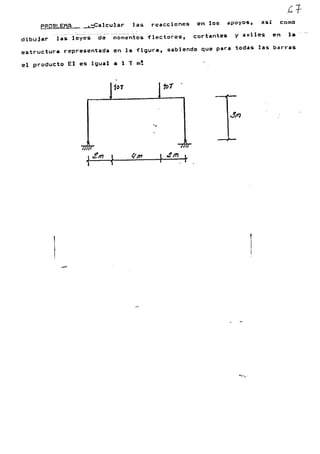
-¡12/Ckeec 7' E-f
d. 7a/b.
/CR. :::.! </G'I l- Y - .i;ce 2L
-
L T - t¡
~A =
.
~ tío- ~. 3 .!L - 7
7 h 7'3-
)
!',:
/
/
fe¡ .
e - - . 0 '"
(Jc - -- - - ,L
1-1 Yt¡ f
C84
::
I
~ - ,':L ::o, Ó
1-+J<¡-S-
- ÓO~k =le
.
(L/ti}.
~(~ i~
r
/ . /
2u./v07,rar< (- "« ,1:);
} (../¡; ;
l., , "-
1,
- -"
J4
"L-=--:~
.
f { .~ ::~ri' y
.h . ~ ¿;,
/
,
)r 1-1, f -Ií
(
~ +~ . J?
", { 4
r~ fI1¡" /f/ -:
Pa6?
-;d'
-/-
a':: 11
ó' :: C.-
~'';'~ ;";.6(
cl1- -
<-.J'-
lo y:? ><.(; ,c-
:::/J
g ::=
'- /2 ]
73
~tJ
JMl¡
at
o
fl'2.
'-
T-tI2.l.
v](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-69-320.jpg)





![~;.~,
...~;{tl~~:~~~t~~'~ff~:~"'"
.:~ é':"
5019
. ~.-:;.~tfBI>- ~ - ¡¿
. ,~
~ "'..0:-, .
.'
"..'< .'. ". - <:',~,
. :
'..r:
.;'¡'.
u~w~::bj:'to~5~~j$~~t1~'_~~f:~~Jq:::;:";'<,::::~::;:'.,
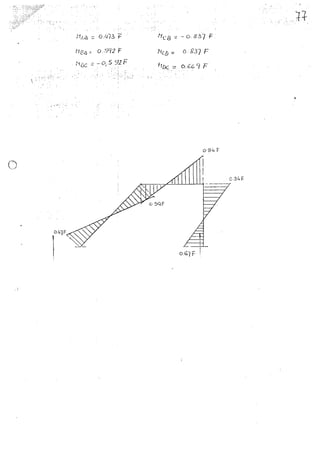
<?'1uiilbrlO de; cork.ks!; "'--
¡ . . '- ,
.
.' ,]
.L
F MBiI
/
,/'
0-/4 /
/
4
x¡JBb He,ó +HAB
40.
~ Hc..D
~
L~~HK1
JDI~odo momentos r¿sp<cf.o a I.
'Zti!)¿ + 11M + '2l1cD t H De =L¡ F
SEIS
Vi
.¡.
2EI$
'2.
T' SE.I9 +2EI9 ~ 4;=
&=
4'2 F = 1?33ln F
i-(¡+ 1!2)EI' El
'L
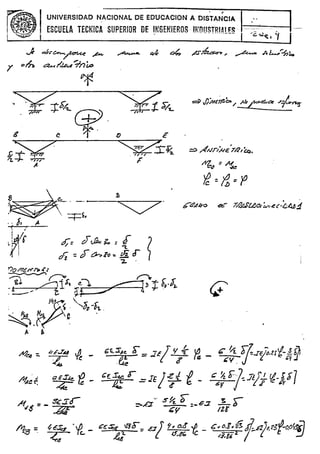
UI3.. :t~2.. Gekrrnlna¿jo e CLnOC¿I))cS .tcc1C_<; Ic-s" .1";("1-'les y yuj".
-Lh ,1',;," b Lv. --j
} de 4:::CbN,](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-77-320.jpg)







![1.5"l
.g c:>
t
J'm
j
1m
l'
1m
+
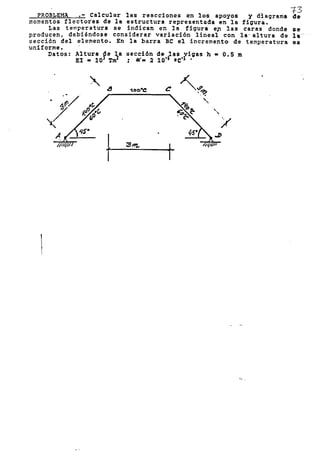
Dt
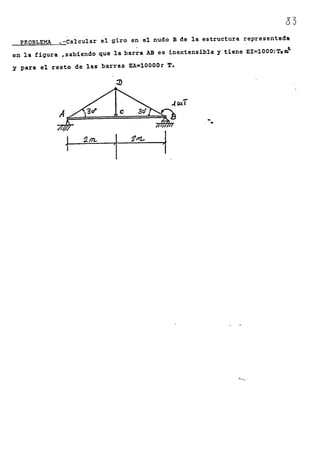
PRJ;lDJ.,J;:t1EL< .' "- Ca 1 cu 1 a,.- --e L (~¡.iJ'''D
_e! F l.__1J~dc--e._~ ?-~-~---~~Q.0'"~:;:'------
~] cSTucr-:o B;' i! e:"i 1.:. t;.arra EF ce la E~tructu¡-a recrES~~-
t2G¿ E~ la f¡gL;ra. saLi~njo qUE 15 b,;ríil AD e °:: inc:>,tens~blC'
CC'l LJn '/a~ c.r de E*¡= 4000" T*me '. '1 par.3 el. resto dE :a.s
t3C-?; E*A= 10000. T.
E F
~-'.](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-88-320.jpg)

![@
~,..
07
UNIVERSIDAD NACIONAL DE EDUCACION A DISTANCIA
ESC~~LA--T~~~l~!J~P_ERI9RJtl~~_E"I~ROS_JNDlI~IRIALES m
3~----
. I ,
~E3Tt:. ~ --b,j"'I1~c.o t
¿;. .fe Leo.
E "F
""~
) ~/..
Srr>T,
~D'~f~
~- 0
(A)
Á)==f.- .-Ec;.~0 ~." U% Á '.
)
AG ~F ; ~/ J<tú,!k~ ~/ ~ ¿ k¡;
~(i:O ,t.2ó r= => ,II~:: If:rF
1 Afe:O -o. ?J"F
"
')
N¡::(!.. '" -o.'+n=
'-,
,
. ;
o,~i1= '~~f~ '
{', ~,S/l1í
A"C- =-
3)'
.tí ~
r
Ú.~n:
(íS)
f t-
C;¡,;
~ ~Ó', e<:
r,;p /.6 ~vi'
,L4 :3'M,1A' ,JZ)
."
, pE. .;zm;1<7E".!~'CL
Co>-..~Cl<'"()0 'DE:. =u..~¡''B~;;o.t..o fm-¡2E.J.V,:~S' ~,xnU(2~S: E.S éD~
d"-l.- Cd<2-2...;/-AtEAD JS'!21"(c:,o,1 OS ~ .B.; ~l.- I-.-l's;~ l¡--
I] ,
'
,
'
"
?'- ~~ ~ jZrF ~ k-c¡-t4 :( ,Le"Le...¿
a. h ;~ J r~ 'u-o rcY~ r~-
~~fd--';J. "
,
'
""TI2A os LI:>C'''
'"
~
"- '1=>E. 6-2 A.1>0 LJ¡,).o:
- I
~"
,
ft:~ ~ ~=6ccoT~
~
't4g:::. '; ~~'t;
,
=
"
,
60
,
16,
"'
,
~o;
,
<>G>o
,
'~ t;':l
l~.er '~,~
~"
~
' "'.,
~:o '- ~t,,1>"D
1", 'E-g~: D-<>-O.=. O. ~ '. ,
L
"
'
, ,
,~<>t-l"eo.o,
""',.
,', ,
~'t?--~z.'T~r
MIJ-, ',*~~TQ¡'~~'J~ ~Q~~~ .
It-I.-I ,
f.. ~:g
~
e.s-~,
6.G
r
<?-
~ o.1'SF o,~T"
".é t '
~
,~¡ ¡
.:¡::"..n¡¿~¡¡:L .
.r_~,--
5"''1: ',' . ,.
'
r-" ~IJtT
~ '
~,
'
~ I~~: o--1
~ 3T
.7- l.',' L.
~"
-===P](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-90-320.jpg)
![l
.
~ -;'~;~E~~'~¡~~A;;;ONAL~~~~~~~~;~~~;;;;;¡~~;¡T
m
'...'1
.-; ESCUELA TECNICASUPERlURDJJN6ENIEROS INDUSTRIALES - -
--'--<- 1 - -.
;- ~ I i
c~~-
í
%- '-7a-<--,{. -.P-«- ¿ / -T~ &=-7h./ g e -
IÚÍ
¡o,~
~1", -
- L-g,--
t
~~
~
O,~~
;j ~~'í
~3
i~
2:TI/=~ ') i~+.c =-~~O.t0=-
,
J'RD~ 0."1 S-1= -3 "
)<W.csTA~DNA -
)
---~ ~
""1
.
~
,
~f.; d-: 7
e
/JI." o~S
S-
::.
.~
]s-
-
-~:7~~
. .4 I
-12<>D
.~
, "':1 'l-Uo)
? ~ 400-0
-
::. "bE>o-D ~I
z.'-
~
IZD"~T
10 -
fJA - -
W~~ 1200
= 6<S:>-ÓT
~ 1."",,-
-,¡¿
"-
. ~ -;1a ~ ~ d-j.-~ ~~~..
,
1~V.t~
.~t
- ,tlt-¡-
7~2&0 .L<A-T
-
j6~
,:'-<'"--:-;'== ~nÍ) --()",~':::..c>
l' - -, é.. - '-.'J-'-.
.- ~ l.-t:..,
(..
~Q
. -
, 1cgl:=- -60-= 1 .
CotJ~ó),~:
- -
QvE p. .t:oL-
l2.0 + ~12.1 ~ D ~ D,i-~1=- S; + ~G-60>-c):::o
"
.
D
{)o o"+~::" ~
Co'j2J'2., 1M~NT6 ~b)C.."1iQ.A
'-
""P2L ~ 1;](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-91-320.jpg)
![- - ~--- --oo.- '.'.0_0-
~..
"o_--, ,--' '---~'-'~-~'--
~~
-~;~;~:~E~~I;A~~~~~~:~:~~~~~;~~~N;~~~~~; "'~-
.
~A 'S ~ !w- ~'G' ("6')
l
1::,~t;8-- rJ"f,E l:- ~ -Ol~ F 1.
!:t:, ,
10000
~ ~r -Vt = VE + o,''1'~-:¡:: /.)
(oe..-o;-
(}j
j6-UU>7 "'-
c:;:Jl.a.k J4:
)
,
fir r:!.'~/n~
, ,
eL~.
.0 -¡:
",--,
'
,
u L 1-'2
~ = el. LJ4", = .!.. IVf:F
- " - +- o=lé
?- "Z- E..6 '-- lcOOc;-
<)
ifa,:fY'';'' ,Kt2 : ,/
ue;);
~,'
.~
¿; U~D, IS
~
()
-c::J-0..<- CoL -0,(;'
-o- ,
AL/:¡t::' - ~ D,~ +V~ D,G.. ,
1."
,'"',,
I 2~
,
4t:::' tJAE ~ =.1:2SF~,
A'E. LO<5>oO. . . (
!
I
II
,'1 - L16~ D
-L
Ve. - ')t. {¡-
'"
.s, '
,~ ~~-Ji au-<k,~, 60' rfl2-'"~~:'
J=-
/.~zr.>o(Os F f- 6.:t-~ '¡,r,
3 " "
"¡,uou
, . . .,~--.N-- -
.-L0~G= ~zLt:>: CcIJ~Qlci0,~ CDMP1STlÚu!~])
~ ~ ~ á:-
~ y.J ~,d
''''r!
~L~¡;~J
4 q.~cu,",.'
o,:::¡n= -.5 '::.
1,'1'bZr-;c,1¡)3t- T c),-=tT'''Ft s-
b=-= 3 '
, l~
~~ F=_'t~4t-~ T~ QlkE-2~ ¿( V6LD'i2.J€. fJEl='](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-92-320.jpg)








![.~ .'~f.f~~~rgt.;i~~~~~:~:~~1F:~:~~;~t!i~~;I'~":';;;"I~
'~, I '--,'''~''
,-, ,- -~ '--'-:""i
V'~
__m
¡ m
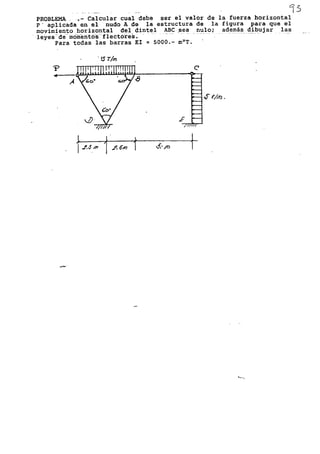
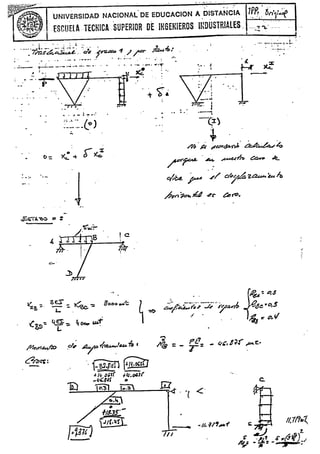
a4<,{. ck ~"á'~~ Y d; éof~izu&.J ok r,t,/
I
0'0
/l/v /'q¡) €
f> '.1
1/$ l3 NUB-o e N l/ 'l7o .])
1:::<:6 = 4 é(2I ~~o¡
U"
: ¡.C,._-= 4 E(21)- o.I{;E
I -v ~....
I
~o
(6C':. ~=o.3!E..!' ~-:: !¡.~Qo.z.~x :
1r ~ -
¿"c.?H. 2~o.'Yi.
&¡= O.~I' ~:: o.~';,
~:: g;~tl:c>zc.Ei
r - I(EJ:' O "",r
-'&0-- -¡:;; =
. <''''-'"
;
'IX;.
~ o, V>3. Cc:1>'" ~nr
,--.
(:) i l.A E. i K- 1:':2)~
:&:..=D.~11 Ccli :: 0,1'4 -
/l. T"-' (.:r)
/ T". :"!.~~.¿~--'-' )
I
IVID,JfÚ.lr~~ ?c u'i?I'P7;2&M/~ .:: ". 1-- ~
I
~E -= /1t-D::
6E&r) ¡- - - 1".'2
(;zr)'1- j
~ -= 110) =
. f€' {2.r)F ~ 1, f 1<..10-:3EX r /l1..T
(]é:)'-
~~;
ta~ a~
'"
,tÍ~
E.:I.. 6' ()T
. .-;:,.
~
¡')?0/17¿'''7/).'' ~ E/HP.1'M,M:l41D. ~
'71) /7fitt'/acJr¡...¿).
~4 = ,...v,7ép'::: ~E.CU) 'J3 - IG, 6'31< :o.3E.:i: p..",T
('U)"2..
,/1ff,J:' H~:= Me 1'{
: ~...': b ~
I 'l.
= 30.. lo'SE~ M:í
I{' l"l.<.)~
tf - M - ~e,Ü~)!1.(3- 16'.'03 ,,¡~3 E.I ",.-;
.
Oe - c.1)- ¡oS0 )1.- - .
-..: ,
"""~~""c"...M
J.I¡ -
'E('Z~'~'2.¡fi -t;C,S'll'ló3&"T':u..;r
""'" "'"
Ac8 ~ ,&c.-- (1.s-) 'L =
~ --..
~',](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-103-320.jpg)
![-- --.,. ,
-
ti.:.::'.;.,;,';;.-:~~i'1!,;~:~~~.;:~~.:, :.. '., "
, '. ..".
EDUCACION
" ..
"
..¡~~ (;UNIVERSIDAD NACIONAL DE A DI?TANCIA .::-') él..
$'~
~"':~.'" -.:."...r .. . .. . ." . -':-0'.-
ESCUElA TEC~!GA SUPERIOR DE mSEmEROS mOUSTRIAlES, 0--
u.n
.
u . ,.. ....
-- ...-- ....- ,,-' u .
---'----
m
,
__.~_m'_-
'--'-'-
..
r-wJf'fJ
8li
[o.lb):;, ~.IJI(
- - 1..2 p.lJl ...E:L--D,lJr !:!i ~ J().D'f
~ D,"'" -o.ltf
"'Il
6,q o.2~ ~
D." ~ -=¡;¡ ¡f~i~.J¡r b
J I~~ -111 :zü -L!3
-¡p' -¡;- o' ~.t
"1OT<i! .,i¡'[" '.~I .1!.f
..L&!» o. t,¡,
6:> t>
-;D.~O -/.41
-;- --;;-
~." -o.!s"
T b
-tP."1 o,or
@ ~
-",or
,-1,'1/]
')
/iL..~f} r:JL~. @ ¡;» )
- ~ '"-A"/.J( -¿, fL
-I,a'-,~I 1, !1. ~:.
, f - ~
- ','V ."r? 0.4 t
a r-r -1.53 - "r¡v -o.:¡:
" - ----f.fl -l. ~ -r...:¡ -I.SJ.
"
~.!T rul' '2,B
- ,-- --~tt J.~~ 1.3; 4.61
II..~ -a,n -¡t.f( I'.'~
--"'. -")---.j c. l/, DH1!! Don) (
~
J:t3
-¡;-
-1,13
#
,.(,
~t14
80
j; &'r
o
-1,",
- ~
p,rl
-r-- Al:"
~fY.Zn
-
ti
-t:','/
./í
¡i?(zf)
.,
'.
0iV&.1dl L-1.f~ P.I~]
----0,°' ~ -
L.8.!l- .Jt)~ .
- o;~
-H,~3 ~~ '--...-
~ ~J~
~Pt6
-r.,~.:;:u I~~~.14 ;3.3'~ -.
o
--tc:a +l.bt ~¡;...~
-1'1.'2.;:tl'~ -_.~
c.~1j1 :D:.~Jjí".~I" 1
o.oz,'-! ? ,-
~ o
.¡ 4.'1.3 .f.~r
-¡;- o
-',01
-D.n
- D"1J,2~ t,n
-, D
-MIC -0.0'
1ó.47.1 b.~1'
1~ l~@-t.f2 -::m; -",:¡ [2;.~rl
t.I~ ..t'... ~r.1 -:::¡---
,.-- - -- -1./;)
1,41 M1. o.'~ ~
-~~ ~ -J!J
,.r.(
- ~ ~. -¡- t>
-1.SJ. 4',f
-l.,:} -Hf
?,~~ .-:- J:.n. -
~J~ "l.!' !'.$~ W
/l4J -CUt -~'.r, I"e"
o?3S' ~,(I~I D,~'1. :o~i¿
D,7 ~
80
;;r'f
-¡;-
-rlfr
-;;-
~,
-D.lf
~
,.
'D"~
ao
". z.z
-..-:!:!1-
t>
D,l(
t>
.4'.'
13(,1.2't:..¡. ..](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-104-320.jpg)



![@' ~~lf~1~r~~~~~W~~Rg~:~~~E~~~~ ~~~~~:~; r: ';:1
~..
..z:~~ :r:
.f"'
b
.
'"TI2t:.S~C4~ L
"..J
f
-
¿E~ r; e ~ ~... 1= :l.2tO,,'(,I¿"Í
L.
z.
I~
"
4:
~-~)-[f1,-~)-y'
K, (~-;;Á)
./
/'/I:~ -TI;(X-,4~:
:f.Z[.~! fiV0.6z(-ZZfD): - 27r; .,.~
!! 1.
:
I
r
/~~tt.t¡ ~)
--=
0.?Q,Q
-
-r!%n. '5
~~~~
~ I(!:¡,~
/7i1{'~J
ú}'CJ>,r-
-
~ ,a:¡,$+ l'i.c.t~¡ ~ 7¡f¡.06..]
o/
.
~
. ~~i:
,-
,.1.
II
"'..
-~
/161. ~:r
- --7Z~ "
+1%("" t)
-¡,.re.
~fZZ(b
.
.. +"ZHb
"
-/1Zf"
-'r~t:)
t::>
o
Z
fíat,f'1-
~ : 4'~ 1;¡M -/.1~) =
.
: -zz~ :fla:¡.r-(zzr,,)) = -/7'C~.:~J
ztJ.g= 1t;Jv'bt! ~ ",n.S- -+-f.¡~'l/~,()6:¡ ~f~:.
./2, = - 8/7¡' '2/[
..](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-108-320.jpg)


![Fi F"".L
¡...::. }
0.1;1
.,.. .'
"-..." ..
. ......~
~:J)
"...
"',
"
.c.
"
/"
,,'
./
,,"
/
..'"
....
./~,
/=d
./,-,,' ,
.'...' 1-
K-
/"
FE; " F5...
-..1 ."JJ .:..
'-
"
I
,"
';
I
b)
D
-u
ro
o
_"F1 LE .- PP.[]Hi '-
IJ/'IDEFDP.t'lED uED"ETR1
t-
:x
.](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-111-320.jpg)








![o'
Jí'I!:
~
or.
~-
..¡.. . ..
..~ :¡
<1
1: ,~
.0.11' I 'o
~
~"'''-?~U_!x ~--
~"",.. 'i z
.
.
ef
b~ ,. O" I
.)<:. ~
óH "'cd. oH
c:ls ..
J
AIzH:i~~ i-
J
A(H~-.fX)~ ~
e:I "
El ,,¡ 2. Z E. 2I
.!! [':';itá'j -+-~
J
CI{I-t.:t-'Px)dx =0
¡? .. 8~t'...
ti
[::J + ~
[H~X-~]: .. O
H
~:
+ ; (H~1- ~;~) ,. O 4 H,t!- p~~o
.24 "
3H=- r~
.!... ./. ~
1r~I:t
1&
. . t ¿
.'r
..
'Q.~I.c,:' ~ c.:.Cea..:::,¡r Ó fC"l' ec..C:CL"n~ &~~h~
11l~ =-r", l.E21..;-
!
el.
.H~, ~+1"4=
~ l.
, e/z;,
,= 2:.r: illt - !ill r
ft.
- Ct : Q.1.
i - ill °t~'
I
a o
!-,
.aH:- ~":'t"
0.'
411 = ~EIi
~.
"'M ':
;a, E:r Ó
Q.2
Se. E'r<f
a~
-,..-,.
I
«""
.'
f'= ~
36EI
,
.6unque eft esle C'a::o "'0 e$ I'I:"cl'S.:1r(o d (&1='0 ~l't:I;l::W~ d codo 9ue /'le~
.se i'.at & corrLmL~nto de nLl'lgul ?u...~o, heno$ 1"I:1a(,~" d u/c.ulo U>n'I" I!ft 1:. pr..c/.'
':'nlcr<=1'
,
.! ~rhr ~ lo ~cl.l~CI podemos dLbllj¿)r la ley de ~ .. ~nle"do en Utt'r
la ~~ "i~ )f lb ¿nHI'"donQ. vo1"(e,,do ~bre /o.!: f...r~ ruh-:bó"r. .! I¡ visto r:;":Ic.d
~~ 'Y c.: oc..'-IOd" & scnl-d" .k d podl~""'o. dibJjck 1;;.dri:,r",~dQ (c. rsh 1d...
cJ.OId.ro °-.,
.](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-120-320.jpg)




![11>
i.~:~~~sl;~~J;A~~~~70:~:~~:~~;;~~~~¡~:_~-
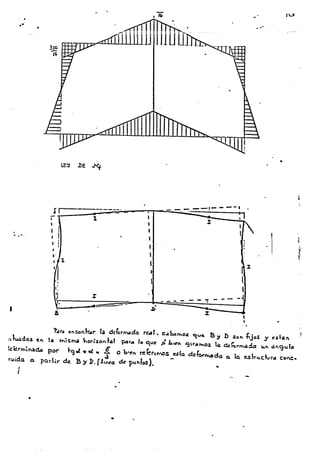
ltou_Jo <>ibu~k.~ /,,# ~ ¿)n ~'
4" =" .roff (d - f-) ,:-, FZ~- I~D f' -:,'F{;-¡¡Z,S .:. ¡,ff,
'
?-t",2
,
<é-:: ':- :&;:;,<v ' , "
"
, ,, , ,
, ,
-.
A[)~:: l~-r
,,2 da)
y;, '" Aj.' EI
~
'
~ ,
1> '
"DF,
'J ,
,11!JA'-=
T ~o
::
,~~ ~o
'
"
'1'.u<¡'k~ <lei ~ .B.'
t? ; 17.J-'¡; + 'LE :r..,o
=<=> =::>
110F ,.3 lJ) ;3 Iv '
JJ :.-ÚD F
rp-- t:I
~
7
1> : "1'1/)1"= P;F - MoF &:: '2 4F'
]'E,J;. s.3 ,
I1/)A =j 8. ~'F -=- -
'Z MrJF-
! -3 D' SI,
,Jc 11 ~ E A
¡
.
':'-3 -l
~=
fo~3 '
(3 Til.-I.¡.3'i.)- FI'I t1Dfr2--
2HX'
4& E:l
-
, ?tI
-
24i-f' - 3~ r - ti !Jw=
'V EJ EJ
(
- '2~1-~ sCr 17.~ _'2Hf" -
-g,F
- '11:-CIf'2,~-'H)=-
- a - w
-
-E.J.
- --0:-', U E'I
- 11Q.~ ,le F
- F ~ f;'r,
lO' 'b'
-
;-! r
- 71:
-
E fq,~
-=
,:g' ¡.. " '
l/Ir" - /!~ r " F fr. )JF~5f. bi ~
Pov- /C«A!u ÁJr =
l(~( f "'1
'-.'
!41)F ~
/1.31 w.í
/ ~,..f
,1, :
' ',
,""
1 ",.
/..~~.," .1 ,](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-127-320.jpg)



![,
/' ,'-
)
i
)
, .~ ¡' .
I Z /.:.:. -'>'
;,..:~;;-
'"
J)
"
e ,."., !""Y1e~ s
--' ,-' ~
!-
JILU
A
-, o",,._'
,--.-..---
~ !;,- ,L~ """
.h"k,.(' ,,'Ir,.:-.;1
-"'-
A'
l-T,
A
._"- 4 I
~
'J'--L'
a;"
~
A
~)
r} l.
rífPW
A(
"~¿ r'f"'o..
I-<-r
;;
5->'r"-.. l-A
.Lt
;.;""'/;<o c<.:
'"
.1) B'
B
e vi e'
~5' , j",.
8 D a'
@ ,
e
e ])'
+
l?S' 7/t..J-
8
I
])
,
' 8'
t j ~ ~ f t
oS' T ~
/'
l '
~,
e
@ ,
-e.1)'
.L/
?61" k-. i. ,
~.J rfw-
1;,', TT: cn-=:o: ¡ T..-:J;
A-
ti
.j)
,,. ,.c-
A'
t !LL~"1'
.(oA
f;{
L '1
r'~'
c.<L-oS
"--~<:--
.
--
, .
' 1'
,/
. .-, . - , . .""~, -,-,"'",'
)v
C C o.-t /.:;.
<
.L
~L.;;>
/
-('¿~~
-
.., <..~.'.J -
/
.J;:..;., ,--fr,'C(J--~-~-~~--
,
.J.f;"/.~'I
.J,'<-A~/.;ta
.c.../'j ...¡ I
,-':'{,;o./fa ~ "a.fJ.
Mfa2c,
]) - ~.
/i-
"](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-131-320.jpg)
![..¡- ~607 .....7
- tJ '1 $'1
~T
,
o '101
u..< T
,
---~-
M
:z ",--- '?:.!.-!-
-
(:z.f~'¡ O) +
,
:iD '-1 "
~J-.>(
(v)'!..
==
/2
E:Ifo'"
,) ~;,:'; r
~
/
.
-
I
,'1 eA
0'1
'-1
8
q.f".
{I/J1-
~
g
o,7J- é-Z- fa
j
~
/1 iJIC. ' == '
'1".E (-¡ <fa -tO) -r o
1/
::
E I 'fa
r
¿ /l{a ~. o -:: 2, f.r- tI 't, - t;3 33
nfa:: ~/2/
?U-<¡,.""~.,¿,.¿, 1I:
I;,.lco~.
~¡J«;¿a .
1". c.""'-/
k"; (.. ...
'
dj
, ~8
l.r,;¿..,J.-t d.P
(",
..L, /;i¡~ ck :
" )
.r-
o? 8'8', "-IT
'¡I(I ::
f'0
".,T
¡vI;A :: - ~
<') 0"1
.
r
¡'-f o
i]c.
O, I Z/
tu T
r .flce
~
I
~=
'2.
0.06/
!
I '
1
'
t1p8
;
l.
/4I;S' ::
1~ () t- tfa) "..
'-/
..
a
,j I
f'1
i!' J>
=
r
/"'f I I =
84
""T
r - - 0/2/
M a'c'
- J
<-( T.
r - 0061
fAc'S'- - I
b) ?;frk..,
~'~L
~--~.t,';h "-
.
2 ,~. ,.~. Lo--<'t,
Ar'(~¡ J~
""T
"-
./7.
v, j
~
y
c ::
¡Z
(; &-<
""
~ i.u-!
- L?"'?
I
~ T
¡) ¡J.¿--r ~~.D J
:: fe, -.
1-
f
1
/
<'-1
.:/.~-</
/ -
,
-,J:"-, l<.~!:
~~/31
o
v.O crh
¡ C'-U'
f;-
1'"-(
.,J
M vi](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-132-320.jpg)





![..::oo:.~. :oo..
.
""".0
,
-"~~'~:'~':~~~ll~~¡~
~n~-
.,'
,--=---...
.'7~. - I,~TM~ 21<[ /" .
.¡. GEI.d .:' ~
Z[ iD 1- O,!:"'<:) G, T "',5 10-1,
]~r' - r;,/" ~
'/¿
'3 t¡- ~'C
~ --,
'C-.-¡iCt;:: ~'.~! 'Pc. + & V'D -:Cf::I~l¡G) ,.
aL 'c tO.!:t;,o ~ - I.S 9]'<t> 1, D' (C4
131-.
-',
Z(..{c -: ° =::2'fe - e +O.S'r",cd- 4.510-4;: o e,) '.
2.2.- EOJltlEt2/0 NUI>o.D
..-.)
Htc ":: -1cr 'f. '.¡. 2 ~:r
~ - 6Er ("g) ::
tcb
J)
leo
~
e¿
hl>D' .:: 2.¡=.r
'fo- == o. s E:r Ifl)
-
eDl>'
H,M =
l¡eI
fJ) T
2.EI
$... bEI ('2"':6T)
~!J8 .e~8
tcls
EJ.1:D° -= 2.50 !f.o + 0.50 'fe -9 ...4.5 ~o-I¡=o (ll
EI[If[)to.~o'Pc - 1.5 9J
= €l ['f,D+ 0.5 9 + 4.5 10-'J
2.3 - ~c.I<IO ~ CCI.:TLI-J'TES
c:
¡
I1~O~HPc.
[1 H,.. He.
" i Ij
~
hCb::: n [if'c +0-5 1f.D-~. 5 9]
~
1"''' '<><-- [ 1D~",-lib E 1 (.),~'i5 'fe: .,.0.315 rJ) -O, ,-;
J -.~
I'1cc: EI (C/'t)~O.S ~ - ¡.S 9] 4
~-
>jt
.
MLE:-H¿c. = -E![ o. 5 ~ + e .¡.4.5 '1ó4 ]
~M.B¿:- hrn} - ~Qt)-:-kl>E ':: -Er [.:>.5'f'b+'2.1619 + 2.5 '::)~J
(C(j ?(1)~'~hc' - ~Er
'
"-B
: 0.5 E.I G
~
Tr;;- & ,- .. -
~ba'
MSJ)= l:l-[O.S'f.t>ofS;-t..'ii.'O''']
"5;:-: L;Er f, - I>U(~4i)
'"
U (o.!:q ~ - L ~:.-"J
T~'E 9 elt:
1
('
¡
e
,
r'!~6l.¡tMeA
= - :;I [0.11:: .¡:. i O,(~.:;,'!ID+o.i~2;.. l. :. ::f'
1](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-138-320.jpg)
![- ::- - ..... --
'~~JJ'; ~"~~~3~ -:~
'
/;~J;:}}/;'¿/Ji~ .:¡
11¿~=-0 . :'
. .
~"~.-
- . .
FI Cp;+ o. S"'fj)-{-?~ + P; i-o.~f, - I.5'S - o..5~ - &-4.5 :..,-:.- c.~ ~ -o:i't'l) .'
-l{._~ 1o-~'- 0,'~7 S:~ -2. 1o-:-~J::o .,'. ,.',
"
:'. .:, '.- -';,;;' ':-.
. ~ :.
'PC ~ lfi> :.. 6.1€:1 g - '-q: '10-'4 =- C;;: (3)'
:", :""
'. -
.' .
"
I?e!.c.lv'lné-o el $1.~J:r~ ob~::n::í.OS:
e:: -(,900 10-"
In -4
T.D::- 2.021 10
)
'Pc:, -2.694 10-4
.! {-:~!, '1)-; 9'1: 1.1'¡:ID-~ 1.G v
IOI.l
Por +an ~ los n,oro..¿"h>.s::
HCA:: 10.000 , 10-4 (-'2,694 - 0:950 +4.500J = O.-gSG. """T
Hc..!)= 1~ 000 -10-lc(-2.6'1:" -1.011 + ~. g50 1 :: - c>.SS5 r :T
NDc ":. (-'2.o21-f.~4t+ 2.850J:: -0.518 ,.,>:T
~
tlD.!)'==- f.011 rrlcT
Hn!.:: (-1.021- O.GSo +4. 500J = !1.529 rn.c T
116B:: -[- l. ~L¡1-1.900 ;. l.¡.500] :: ~I. '253 ,.,,,T
..
'.
~,
!.("-
I-i.t,;: -:: 1. 2~3 I'r:>(T
o
Ne.¡:.' ::-o.Cj50 M>tT
I":?ib:: (-~.011-1.C¡oo~4.5001:: I.Sqo rn"T
NE.!:: (- l.'Zq - 2, oo~J = - 3. 2E.1-
MOL=- (-~.O11-4.111 -+'2.5J :: 2.628 f'rI1<.
f
l.,." - - '26 "''' ii,..:.w- .-~
? '-
..
u- - u_u -'--------
.__h_--'-.-----.-.----..-...---](https://image.slidesharecdn.com/probres-151021135236-lva1-app6891/85/Prob-res-139-320.jpg)
