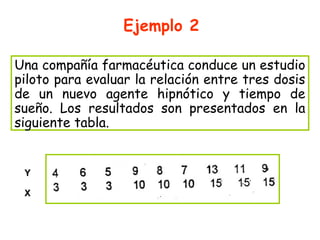
El documento presenta un análisis de regresión lineal simple para predecir las ganancias anuales de una compañía en función de la cantidad gastada en investigación y desarrollo. Se muestran datos de 11 años que relacionan el gasto en I+D y las ganancias. El vicepresidente podría usar la ecuación de regresión lineal estimada a partir de estos datos para sustentar su teoría de que las ganancias dependen de la inversión en I+D.

1. ANÁLISIS DE
REGRESIÓN

2. Introducción
• El vicepresidente de una gran
compañía opina que las ganancias
anuales de la empresa dependen de
la cantidad gastada en investigación
y desarrollo. El presidente de la
compañía no está de acuerdo y ha
solicitado pruebas.

3. • ¿Qué herramienta puede presentar el
vicepresidente que sustenten su teoría?
• ¿Qué variables tendrá que medir?
• ¿Qué ecuación ayudará a predecir las
ganancias anuales en función de la
cantidad presupuestada en I y D?
• ¿Será esta ecuación lineal o no lineal?
• ¿Qué precisión se puede esperar al usar
esta herramienta de toma de decisiones?

4. Año
Gasto en I y D
(ciento de
miles )
Ganancia
anual
(millones)
1999 2 20
2000 4 25
2001 5 34
2002 4 30
2003 6 33
2004 5 34
2005 5 36
2006 7 35
2007 8 40
2008 7 37
2009 8 41
A continuación se presentan datos de 11 añosA continuación se presentan datos de 11 años
¿Una línea recta podría ser lo
más adecuado para relacionar
estas variables?
0
10
20
30
40
50
0 2 4 6 8 10

5. Si sabemos que existe una relación entre una variable
denominada dependiente y otras denominadas
independientes (como por ejemplo las existentes
entre: la experiencia profesional de los trabajadores
y sus respectivos sueldos, las estaturas y pesos de
personas, la producción agraria y la cantidad de
fertilizantes utilizados, etc.), se suele recurrir a los
estudios de regresión.

6. Objetivo
Estudio de la relación funcional entre dos variables.
Establecer una relación cuantitativa entre dos o más
variables relacionadas.
Se trata de PREDECIR y/o EXPLICAR el valor de una
variable (v. Dependiente), dado el valor de otra(s)
variable(s) relacionada(s) (v. Independiente(s)).
Las variables X e Y deben ser de naturaleza
cuantitativa y de preferencia continua.

7. REGRESIÓNREGRESIÓN
LINEAL SIMPLELINEAL SIMPLE

8. Qué es el análisis
de regresión
lineal ?
Es modelar la dependencia de la variable Y
en función de la variable X a través de la
ecuación de una recta
Análisis de Regresión Lineal Simple
0 1i i iY X eβ β= + + i=1, 2, …, n
Variable
dependiente
Variable
predictora
(independiente)
Parámetros
Error ~ NID(0,σ2
)

9. Ecuación de la recta
a: Ordenada en el origen o intercepto,
distancia entre el origen y el punto en que la
recta corta al eje Y, puede ser +, - ó 0.
b: Coeficiente de regresión, expresa la
cantidad en la que varía Y cuando X aumenta
en una unidad, puede ser +, - ó 0

10. Mediante la recta de regresión podríamos
obtener de manera aproximada el valor de la
variable dependiente (y) de la que conociéramos
la variable independiente (x), en una población
semejante a aquella de la que se ha obtenido la
muestra.
De manera más precisa, si conocemos la
expresión de la recta de regresión, se pueden
calcular valores para la variable y, conocidos los
de x, como si se tratara de una función.
Utilidad que tiene la recta de
regresión

11. ESTIMACIÓN DEL MODELO DE REGRESIÓN LINEALESTIMACIÓN DEL MODELO DE REGRESIÓN LINEAL
SIMPLESIMPLE
Consiste en determinar los valores de "a" y "b " a partir de la
muestra, es decir, encontrar los valores de a y b con los datos
observados de la muestra. El método de estimación es el de
Mínimos Cuadrados, mediante el cual se obtiene:
Luego, la ecuación de regresión
muestral estimada es

12. CÓMO SE INTERPRETAN LOSCÓMO SE INTERPRETAN LOS
PARÁMETROSPARÁMETROS
Se interpretan como:
aa es el valor estimado de la variable Y cuando la
variable X = 0
bb es el coeficiente de regresión que está expresado
en las mismas unidades de Y por cada unidad de X.
Indica el número de unidades en que varía Y cuando
se produce un cambio en una unidad en X.

13. ¿Qué tan bueno es el modelo?
Coeficiente de determinación
Porcentaje de la variabilidad de Y que es explicada por la ecuación
de regresión ajustada.
> 0.70 entonces, el modelo es adecuado.
Donde: r= coeficiente de correlación lineal.

14. EJEMPLO 1:
El dueño de una licorería está interesado en medir el efecto del
precio de las botellas de whisky escocés sobre la cantidad vendida.
Los resultados de la tabla adjunta se obtuvieron de una muestra
aleatoria de las ventas de ocho semanas. El precio está medido en
dólares y las ventas en cajas:
PRECIO 192 205 197 213 208 199 178 172
VENTAS 25 14 18 12 11 15 29 35
A. Estimar la recta de regresión
para las ventas.
B. Estimar cuánto será la cantidad
vendida si el precio de la caja es
de 200 dólares.

15. Resolviendo:
Precio Ventas XY X2
192 25
205 14
197 18
213 12
208 11
199 15
178 29
172 35
Totales

16. Reemplazando los valores tenemos:
xY
XbYa
XnX
YXnXY
b
Y
X
n
5963.04545.136
4545.1365.195)5963.0(875.19
5963.0
5.1958307200
875.195.195830227
875.198/159
5.1958/1564
8
__
2_
22
__
_
_
−=
=×−−=−=
−=
×−
××−
=
−
−
=
==
==
=
∧
∑
∑
Por cada dólar que incrementa el precio de la botella de
whisky las ventas disminuye en 0.5963 cajas.

17. Coeficiente de Determinación (R2
) (%)
 Indica el porcentaje de variabilidad en los datos de Y
que están explicados por la regresión lineal sobre X. Si
tenemos el valor del coeficiente de correlación ( r ),
entonces R2
es el valor de r elevado al cuadrado.
También se calcula en base a la siguiente formula:
Este valor multiplicar por 100 para
expresar en porcentaje

18. Ejemplo 2
Una compañía farmacéutica conduce un estudio
piloto para evaluar la relación entre tres dosis
de un nuevo agente hipnótico y tiempo de
sueño. Los resultados son presentados en la
siguiente tabla.
XX
YY

19. Diagrama de dispersión o de puntos
En el diagrama de
puntos se aprecia
una relación lineal
positiva o directa
entre ambas
variables.
Modelo de
regresión lineal:
y = a + b x

20. Cálculos previos

21. Por consiguiente, el modelo de
regresión estimado es:
Interpretación:
Por cada 1 nM/kg en la dosis del agente
hipnótico, el tiempo de sueño aumenta en 0.5
horas.

22. Y el coeficiente de determinación es:
Interpretación:
1. El tiempo de sueño está explicado en un
81.07% por la dosis del agente hipnótico
ingerida.
2. El modelo explica en 81.07% el tiempo de
sueño.
%07.812
=R

23. EJEMPLO PROPUESTO:
Los datos de la siguiente tabla representan las estaturas (X,
cm) y los pesos (Y, kg) de una muestra de 12 hombres
adultos. Para cada estatura fijada previamente se observó el
peso de una persona seleccionada de entre el grupo con dicha
estatura, resultando:
La ecuación de regresión estimada es:
Coeficiente de correlación: R= 0.9379
Coeficiente de determinación: R²=0.8796

24. El valor de b = 0.8676 indica el incremento del peso en
kilogramos, en promedio, por cada centímetro de aumento
en la estatura de los hombres adultos.
El valor de a, no tiene interpretación práctica en el ejemplo,
se interpretaría como el valor obtenido, en promedio, para
el peso Y, cuando la estatura es 0.