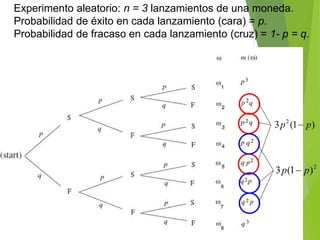
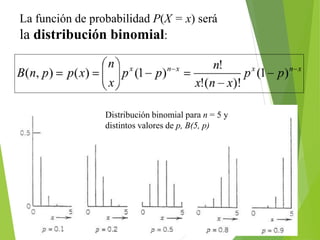
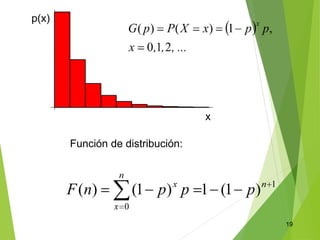
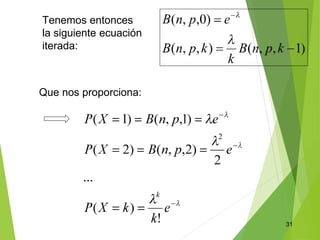
Este documento describe diferentes distribuciones de probabilidad discretas como la binomial, la geométrica, la binomial negativa y la de Poisson. Explica conceptos como la función de probabilidad, la media, la varianza y la desviación estándar para estas distribuciones. También incluye ejemplos numéricos y ejercicios resueltos para ilustrar el cálculo de probabilidades usando estas distribuciones.

1. 1
DIVISION DE CIENCIAS ECONOMICO ADMINISTRATIVAS
Arq. Juan Martín Muñoz Hernández
Nov. 2017
ESTADISTICA DESCRIPTIVA

2. 2
Se denomina distribución de variable discreta a aquella cuya función
de probabilidad sólo toma valores positivos naturales en un conjunto de
valores de {x│x} finito o infinito numerable. A dicha función se le llama
función de densidad de probabilidad
Función de probabilidad
Se llama función de probabilidad de una variable aleatoria discreta X a
la aplicación que asocia a cada valor de xi de la variable su
probabilidad pi.
0 ≤ pi ≤ 1
p1 + p2 + p3 + · · · + pn = Σ pi = 1
Distribuciones discretas

3. 3
Distribuciones discretas
Parámetros de la distribución de probabilidad
Media, valor esperado o esperanza matemática
Desviación Estandar
Varianza

4. 4
Una variable aleatoria X puede tomar los valores 30, 40, 50 y 60 con probabilidades de
0.4, 0.2, 0.1 y 0.3 respectivamente.
a.Calcular la esperanza matemática de la v. a. X
b.Calcular su varianza
c.Calcular la desviación estándar de la v. a. X
EJEMPLO
a) tomando en consideración los valores y sustituyéndolos en la
fórmula µ=(30*0.40)+(40*0.20)+(50*0.10)+(60*0.30) =12.00 + 8.00 +
5.00 + 18.00 =43.00
b) σ2
= 360 + 320 + 250 + 1080 − 1849
= 2010 – 1849 = 161
c) σ = 161 =12.688

5. 5
Distribución de Bernoulli
Experimento de Bernoulli: Admite solo
dos resultados: éxito o fracaso. Y
podemos, definer, a la variable aleatoria
discreta X tal que:
éxito → 1
fracaso → 0
Si la probabilidad de éxito es p la de fracas será q=(1 – p),
podemos construir una función de probabilidad:
Un típico experimento de Bernoulli es el lanzamiento de
una moneda con probabilidad p para cara y (1-p) para
cruz. De donde la prob. De èxito equivale al 50% y la de
fracaso 50%

6. 6
Función de distribución:

7. 7
Ejercicio: Calcular la esperanza y la varianza
de la distribución de Bernoulli.

8. 8
Distribución binomial
La distribución binomial aparece cuando estamos
interesados en el número de veces que un suceso
A ocurre (éxitos) en n intentos independientes de
un experimento.
P. ej.: # de caras en n lanzamientos de una moneda.
Si A tiene probabilidad p (probabilidad de éxito) en
un intento, entonces 1-p es la probabilidad de que A
no ocurra (probabilidad de fracaso).

9. 9
Experimento aleatorio: n = 3 lanzamientos de una moneda.
Probabilidad de éxito en cada lanzamiento (cara) = p.
Probabilidad de fracaso en cada lanzamiento (cruz) = 1- p = q.

10. 10
Supongamos que el experimento consta de n
intentos y definamos la variable aleatoria:
X = Número de veces que ocurre A.
En nuestro ejemplo: X = Número de veces que sale cara.
Entonces X puede tomar los valores 0, 1, 2, ... n.
Si consideramos uno de estos valores, digamos el
valor x , i.e. en x de los n intentos ocurre A y en n - x
no. Entonces la probabilidad de cada posible
ordenación es pxqn-x y existen idénticas
ordenaciones.

11. 11
La función de probabilidad P(X = x) será
la distribución binomial:
Distribución binomial para n = 5 y
distintos valores de p, B(5, p)

12. 12

13. 13
Ejercicio:
¿Cuál es la probabilidad de que en una familia de 4 hijos
exactamente 2 sean niñas?

14. 14
Ejercicio:
Si una décima parte de las personas tienen cierto grupo
sanguíneo, ¿cuál es la probabilidad de que entre 100
personas escogidas al azar exactamente 8 de ellas
pertenezcan a este grupo sanguíneo?

15. 15
¿Y si la pregunta es 8 como máximo?

16. 16
Calcula la probabilidad de obtener al menos dos seises al
lanzar un dado cuatro veces.
p = 1/6, q = 5/6, n = 4
Al menos dos seises, implica que nos valen k = 2, 3, 4.
P(2) + P(3) + P (4)

17. 18
Distribución geométrica
Consideremos el siguiente experimento:
Partimos de un experimento de Bernoulli donde la
probabilidad de que ocurra un suceso es
p (éxito) y la probabilidad de que no ocurra
q = 1- p (fracaso). Repetimos nuestro experimento
hasta conseguir el primer éxito. Definimos la variable
aleatoria X, como el número de fracasos hasta que
se obtiene el primer éxito. Entonces:

18. 19
p(x)
x
Función de distribución:

19. 20
Distribución binomial negativa
(de Pascal o de Pólya)
Consideremos el siguiente experimento:
Partimos de un experimento de Bernoulli donde la probabilidad
de que ocurra un suceso es p (éxito) y la probabilidad de que
no ocurra q = 1- p (fracaso). Repetimos nuestro experimento
hasta conseguir el r-ésimo éxito. Definimos la variable
aleatoria X, como el número de fracasos x hasta que se
obtiene el r-ésimo éxito. Entonces:
Se denomina binomial negativa porque los coeficiente provienen de
la serie binomial negativa:
El último tiene que ser un éxito.

20. 21
Distribución binomial negativa
(de Pascal o de Pólya)
La distribución binomial negativa también se puede definir
como el número de pruebas x hasta la aparición de r éxitos.
Como el número de pruebas x, en este caso, contabiliza
tanto los éxitos como los fracasos se tendría según ésta
definición que:

21. 22
Disponemos de una moneda trucada con probabilidad de cara
igual a p=0.25. La lanzamos hasta que obtenemos 2 caras.
La distribución del número de lanzamientos x será:
x
P(x)

22. 23
Elegir al azar con reemplazo
Elegir al azar con reemplazo significa que escogemos al azar
un elemento de un conjunto y lo regresamos para elegir de nuevo
al azar. Esto garantiza la independencia de las elecciones y nos
lleva a una distribución binomial.
Si una caja contiene N bolas de las cuales A son rojas, entonces
la probabilidad de escoger al azar una bola roja es: p = A/N.
Si repetimos el experimento sacando n bolas con reemplazo la
probabilidad de que x sean rojas es:
(Una distribución binomial)

23. 24
Elegir al azar sin reemplazo
Elegir al azar sin reemplazo significa que no devolvemos
el elemento elegido al azar al conjunto. De modo que las
probabilidades de la siguiente elección dependen de las
anteriores.
Si repetimos el experimento anterior sacando n bolas sin
reemplazo, ¿cuál será ahora la probabilidad de que x sean
rojas?
Para calcular los casos favorables observa que:
N = A + (N – A). De las A bolas rojas tomaremos x y de
las N – A bolas no rojas tomaremos n – x.

24. 25
Distribución hipergeométrica

25. 26
Queremos seleccionar al azar dos bolas de una caja que contiene
10 bolas, tres de las cuales son rojas. Encuentra la función de
probabilidad de la variable aleatoria : X = Número de bolas rojas
en cada elección (con y sin reemplazo).
Tenemos N = 10, A = 3, N - A = 7, n = 2
Escogemos con reemplazo:
Escogemos sin reemplazo:

26. 28
Distribución de Poisson
Cuando en una distribución binomial el número de intentos (n)
es grande y la probabilidad de éxito (p) es pequeña, la
distribución binomial converge a la distribución de Poisson:
Observa que si p es pequeña, el éxito es
un “suceso raro”.
La distribución de Poisson, junto con la uniforme y la
binomial, son las distribuciones más utilizadas.
donde np = λ

27. 29
Un proceso poissoniano es aquél compuesto de
eventos discretos que son independientes en el
espacio y/o en el tiempo.
Por ejemplo la llegada de fotones a un detector.
Usemos la distribución binomial para modelar el
proceso. Podemos dividir el intervalo de tiempo en el
que ocurre el proceso en n subintervalos suficientemente
pequeños, como para asegurarnos que a lo sumo se
produce un evento en cada subintervalo. De modo que
en cada subintervalo, o se producen 0 o 1 ocurrencias.
A lo sumo llega un fotón en cada subintervalo o ninguno.
De modo que podemos entender el proceso como un
experimento de Bernoulli. Para determinar p, podemos
razonar de la siguiente manera:

28. 30
En promedio se producirán λt ocurrencias en un intervalo de
tiempo t. Si este intervalo se divide en n subintervalos,
entonces esperaríamos en promedio (usando Bernoulli):
np ocurrencias. Así: λt = np, p = λt / n.
Sin pérdida de generalidad supongamos que t = 1 y que X
es la variable aleatoria = número total de ocurrencias.
Sabemos que:
Observa que para n grande P(X = 0) es aproximadamente e-λ.
Además para n grande (y por tanto p muy pequeño):

29. 31
Tenemos entonces
la siguiente ecuación
iterada:
Que nos proporciona:

30. 33
Distribución de Poisson para varios valores de μ.
La distribución de Poisson se obtiene como aproximación de
una distribución binomial con la misma media, para ‘n grande’
(n > 30) y ‘p pequeño’ (p < 0,1). Queda caracterizada por un
único parámetro μ (que es a su vez su media y varianza).
μ = σ = n p = λ

31. 34
Si la probabilidad de fabricar un televisor defectuoso es
p = 0.01, ¿cuál es la probabilidad de que en un lote de 100
televisores contenga más de 2 televisores defectuosos?
El suceso complementario Ac: No más de 2 televisores
defectuosos puede aproximarse con una distribución de
Poisson con μ = np = 1, sumando p(0) + p(1) + p(2).
La distribución binomial nos daría el resultado exacto:

32. 35
La señal promedio recibida en un telescopio de una fuente
celeste es de 10 fotones por segundo. Calcular la probabilidad
de recibir 7 fotones en un segundo dado.
P(7) = 107 e−10 / 7! = 0.09, es decir 9%
Parece muy baja. Comparemos con el valor de máxima
probabilidad que ocurrirá para x = 10:
μ = 10 P(10) = 1010 x e−10 / 10! = 0.125, es decir 12.5%
Las probabilidades poissonianas para un número de eventos
dado, son siempre pequeñas, incluso en el máximo de la
distribución de probabilidad.
Una distribución de Poisson
con μ = 10.

33. 36
Si en promedio, entran 2 coches por minuto en un garaje, ¿cuál
es la probabilidad de que durante un minuto entren 4 o más
coches?
Si asumimos que un minuto puede dividirse en muchos
intervalos cortos de tiempo independientes y que la probabilidad
de que un coche entre en uno de esos intervalos es p – que para
un intervalo pequeño será también pequeño – podemos
aproximar la distribución a una Poisson con μ = np = 2.
y la respuesta es 1 – 0.857 = 0.143
El suceso complementario “entran 3 coches o menos” tiene
probabilidad: