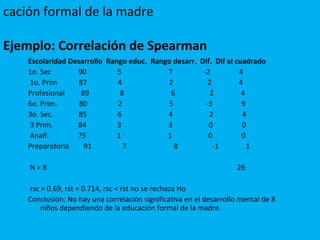
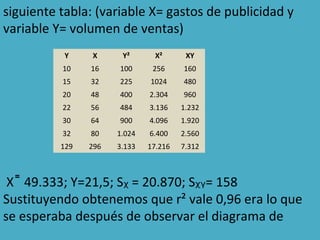
Este documento explica los conceptos básicos de la regresión lineal simple y múltiple. La regresión lineal es una técnica estadística que se usa para modelar la relación entre una variable dependiente y una o más variables independientes. Se utiliza para predecir valores de la variable dependiente y cuantificar el efecto de las variables independientes. El documento describe cómo construir los modelos de regresión lineal y múltiple, incluidas las fórmulas y suposiciones involucradas.

1. 2014

2. Introducción
El análisis de regresión es una técnica estadística
usada para estudiar la relación entre variables. En la
investigación social se utiliza para predecir una
amplia gama de fenómenos, desde medidas
económicas hasta diferentes aspectos del
comportamiento humano.
Tanto en el caso de dos variables (regresión simple)
como en el de más de dos variables (regresión
múltiple), el análisis de regresión se usa

3. para explorar y cuantificar la relación entre una
variable llamada dependiente o criterio (y) y una o
más variable llamadas independiente o predictoras
(X₁, X₂ …Xκ), así como para desarrollar una ecuación
lineal con fines predictivos.
Regresión lineal Simple
Es un modelo matemático para predecir el efecto de
una variable sobre otra, ambas cuantitativas.
Una variable es la dependiente y la otra
independiente. Se gráfica con el diagrama de
dispersión .
Dice como es la relación entre las dos variables.

4. El análisis consiste en encontrar la mejor línea recta
de esos puntos.
La variable X o independiente o predictora, la
variable Y es la variable dependiente o predicha
 Los valores de X son fijos (previamente
seleccionados por el investigador)
Para cada X existe un conjunto de valores de Y, que
deben seguir una distribución normal es decir las
valores de Y deben ser normales , para aplicar con
validez los procedimientos de inferencia y/o
estimación
Todas las varianzas de las subpoblaciones de Y

5. son iguales.
 La relación se puede representar gráficamente
mediante una línea recta
Se supone que el error sigue una distribución normal
con media cero y sigma²
 El modelo de regresión completo es
Y es el valor de la variable dependiente
A o alfa es el intercepto, donde cruza el eje Y
B o beta es la pendiente o inclinación
Diagrama de Dispersión
exy ++= βα

8. El análisis de regresión múltiple es el estudio de la
forma en que una variable dependiente, γ, se
relaciona con dos o más variables independientes.
En el caso general emplearemos k para representar
la cantidad de variables independientes.
Los conceptos de un modelo de regresión y una
ecuación de regresión que presentamos

9. presentamos en el tema anterior se pueden aplicar
al caso de la regresión múltiple. La ecuación que
describe la forma en que la variable dependiente, γ,
se relaciona con las variables independientes χ1,
χ2 ,...,χk y un término de error se llama modelo de
regresión. El modelo de regresión múltiple tiene la
forma siguiente:
kk xbxbxbby ++++= ...ˆ 22110

10. VARIABLE DEPENDIENTE (Y) VARIABLES INDEPENDIENTES (X1,X2,......)
Volumen de ventas, en unidades Precio unitario
Gasto de Propaganda
Peso de los estudiantes Estatura
Edad
Consumo de bienes industriales por año Ingreso disponible
Importación de bienes de consumo
Unidades consumidas de un bien por
familia
Precio unitario del bien
Ingreso
Número de integrantes por familia
Precio de una vivienda Nº de habitaciones
Nº de pisos
Área construida
Área techada , etc.

11. Análisis de regresión múltiple para 2 variables
independientes
Para dos variables independientes, la formula general
de la ecuación de la regresión múltiple es:
 X₁ y X₂ son las variables independiente
A es la intecepción en Y
Y a b X b X' = + +1 1 2 2
b1 es el cambio neto en Y para cada cambio
unitario en X1, manteniendo X2 constante

12. Se denomina coeficiente de regresión parcial,
coeficiente de regresión neta o bien coeficiente de
regresión.
B₂ es el cambio neto en Y para cada cambio unitario
en X₂, manteniendo X₁ constante. Se denomina
coeficiente de regresión parcial o bien coeficiente de
regresión.
El cálculo de ésos valores es por demás laborioso a
mano

13. Análisis de regresión múltiple con k variables
independientes.
La ecuación general de regresión múltiple con k
variables independientes es:
El criterio de mínimos cuadrados se usa para el
desarrollo de esta ecuación.
Como estimar b₁, b₂, etc., es muy tedioso, existen
muchos programas de cómputo que pueden utilizarse
para estimarlos
Y a b X b X b Xk k' ...= + + + +1 1 2 2
Error estándar múltiple de la estimación

14. Error Estándar Múltiple de la Estimación de regresión
El error estándar múltiple de la estimación es la
medida de la eficiencia de la ecuación
Está medida en las mismas unidades que la variable
dependiente
Es difícil determinar cuál es un valor grande y cuál es
uno pequeño para el error estándar
La formula es:
Donde
Y es la observación
Y es el valor estimado en la ecuación de regresión′
)1()1(
)'( 2
12
+−
=
+−
−
= ∑⋅⋅⋅⋅
kn
SSE
kn
YY
S kY

15. n es el número de observaciones y k es el número de
variables dependientes.
Regresión y correlación múltiple (suposiciones)
Las variables independientes y dependientes tienen
una relación lineal
La variable dependiente debe ser continua y al menos
con escala de intervalo
La variación en (Y - Y ) o residuo debe ser la misma′
para todos los valores de Y
Cuando éste es el caso, se dice que la diferencia
presenta homoscedasticidad
Los residuos deben tener distribución normal con
media igual a 0

16. Las observaciones sucesivas de la variable
dependiente deben estar correlacionadas.
La matriz de correlación se usa para mostrar todos los
posibles coeficientes de correlación simple entre
todas las variables.
La matriz también es útil para analizar y localizar la
correlación de las variables independientes.
En la matriz se muestra qué tan fuerte están
correlacionadas las variables independientes, con la
variable dependiente.
También es útil para verificar si existe correlación
entre las variables independientes Multicolinealidad
lo cual distorsionaría el error estándar

17. Enfoque Matricial
Donde:
βXy =
1
3
2
1
.
.
.
xnny
y
y
y
y






















=
pnnkiii
k
k
k
x
xxxx
xxxx
xxxx
xxxx
X






















=
.......1
........................
........................
........................
.......1
.......1
.......1
321
3333231
2232221
1131211
1
2
1
0
.
.
.
xpkb
b
b
b






















=β

18. Enfoque Matricial para Encontrar los Parámetros de la
Ecuación de Regresión.
Al ajustar un modelo de regresión múltiple es mucho
más conveniente expresar las operaciones
matemáticas en forma matricial. Supongamos que
existen k variables independientes y n observaciones
(X₁ , X₂, X₃….X¡ĸ, Y¡), i= 1, 2, 3, 4, …., n, y que el
modelo que relaciona las variables independientes y
la variable dependiente es:
Este modelo es un sistema de n ecuaciones que
pueden expresarse en notación matricial como:
ikkiii xbxbxbby ++++= ...ˆ 22110

19. Correlación simple
es una extensión de la regresión simple
Mide la calidad de ajuste de una línea.
Dice cuanto se relacionan los datos variables
R es el coeficiente de correlación.
R² es el coeficiente de determinación
prueba de Hipótesis
Ho; r=0, mediante la estadística F
Si r es igual cero se concluye que no existe
correlación entre las variables, pero puede ser no
totaliación
licadainiación
r
var
expvar2
=

20. Lineal (exponencial, curva, etc.)
Coeficiente de Pearson.
puede variar de -1 a + 1
-1 correlación negativa perfecta
-0,9 correlación negativa muy fuerte
-0,75 correlación negativa considerable
-0,5 correlación negativa media
-0,1 correlación negativa débil
0,0 no existe correlación entre las variables
Los programas reportan el valor de p del coeficiente
de para evaluar la significancia de la correlación

22. Ejemplo de regresión lineal simple
Temperatura media anual y tasa de mortalidad por
100,000 habitantes
y = -0,0592x + 4,6146
R2
= 0,8395
-0,5
0
0,5
1
1,5
2
2,5
0 20 40 60 80 100
Temperatura
Tasademortalidadpor
100,000

23. Correlación de Spearman
Son medidas de correlación para dos variables, por lo
menos una de ellas es ordinal
Los individuos u objetos se ordenan por rangos
(jerarquías)
Objetivo. Conocer si el desarrollo mental de 8 niños
está asociado a la educación formal de su madre.
Hipótesis.
Ho. No habrá correlación significativa en el desarrollo
mental de 8 niños dependiendo de la educación
formal de la madre
H1. Habrá una correlación significativa en el
desarrollo mental de 8 niños dependiendo de la edu-

24. cación formal de la madre
Ejemplo: Correlación de Spearman
Escolaridad Desarrollo Rango educ. Rango desarr. Dif. Dif al cuadrado
1o. Sec 90 5 7 -2 4
1o. Prim 87 4 2 2 4
Profesional 89 8 6 2 4
6o. Prim. 80 2 5 -3 9
3o. Sec. 85 6 4 2 4
3 Prim. 84 3 3 0 0
Analf. 75 1 1 0 0
Preparatoria 91 7 8 -1 1
N = 8 26
rsc = 0.69, rst = 0.714, rsc < rst no se rechaza Ho
Conclusión: No hay una correlación significativa en el desarrollo mental de 8
niños dependiendo de la educación formal de la madre.

25. Caso: correlación de Spearman
Material y Método: se realizó un estudio transversal
y comparativo aplicado a una población de 21
departamentos del Perú realizada en forma aleatoria
(37 hospitales y 21 Centros de Salud Cabeceras de
red). Se utilizaron dos instrumentos: Encuesta de
satisfacción del establecimiento de salud a puérperas
usuarias de los establecimientos y la Lista de chequeo
para la medición de procesos de calidad de atención
en servicios materno prenatales. Para el análisis de
los datos se realizó un análisis bivariado y se utilizó el
coeficiente de correlación de Spearman.
Resultados: El coeficiente de correlación de
Spearman entre el Grado de de satisfacción de la

26. servicios de atención de parto y el Porcentaje de
<cumplimiento del Protocolo de Atención de Parto
resultó de 0.027, lo que revela la no existencia de
relación directa entre dichas variables.
Conclusiones: se demuestra la falta de correlación
entre el nivel de satisfacción de usuarias y el nivel de
cumplimiento de índices estandarizados de atención
del parto en los Centros Hospitalarios.

27. Ejercicio de Regresión lineal de dos variables
De una determinada empresa se conocen los
siguientes datos, referidos al volumen de ventas
( en millones de pesetas) y al gasto en publicidad
( en miles de pesetas) de los últimos 6 años:
Volumen de Ventas (mill pesetas) Gastos en Publicidad (mil de pesetas
10 16
15 32
20 48
22 56
30 64
32 80

28. a) ¿Existe una relación lineal entre las ventas de la
empresa y los gastos de publicidad?
Razona la respuesta
b) Obtener las rectas de regresión mínimo cuadrático
c) ¿Qué volumen de ventas de la empresa se podría
esperar en un que se gaste en publicidad 60.000
pesetas?
d) Si lo único que interesase fuese la evolución del
volumen de ventas en términos de gastos de
publicidad, sin tener en cuenta la cantidad concreta
de cada una de ellas ¿existiría correlación ordinal
entre ambas variables?

29. Observándolo podemos decir que existe relación
lineal entre ambas variables.
Ahora calculamos el coeficiente de determinación
lineal para obtener una medida descriptiva del grado
de asociación lineal que existe entre las variables. La
expresión del coeficiente de determinación es:
R² = S²ᵪᵧ/S²ᵪᵧ x s²ᵧ
Donde Sᵪᵧ representa la covarianza de las variables X
e Y. Cuya expresión simplificada es:
Sᵪᵧ =
Para clarificar la forma de cálculo construimos la
yx
n
yx ii
*−
∑

30. siguiente tabla: (variable X= gastos de publicidad y
variable Y= volumen de ventas)
X 49.333; Y=21,5; S˭ ᵪ = 20.870; Sᵪᵧ= 158
Sustituyendo obtenemos que r² vale 0,96 era lo que
se esperaba después de observar el diagrama de
Y X Y² X² XY
10 16 100 256 160
15 32 225 1024 480
20 48 400 2.304 960
22 56 484 3.136 1.232
30 64 900 4.096 1.920
32 80 1.024 6.400 2.560
129 296 3.133 17.216 7.312

31. Dispersión
b) Si expresamos las rectas de regresión como y= a+bx
y x*=c + dy los coeficiente de los calculados son
como:
; a= -b x ;ẋȳ
c= - d x ȳ
aplicándolas a este problema obtenemos la recta de
regresión :
Y*= 3.604 + 0,363x ; X* = -7.356 + 2.637y
2
x
xy
S
S
b =
2
x
xy
S
S
d =
x

32. c) Para realizar la predicción del volumen de ventas
utilizamos la recta de regresión que tienen las ventas
en función de los gastos en publicidad. Para un gasto
en publicidad de 60000 pesetas obtendremos un
volumen de ventas de x* =3.604+0.363*60=25.384
millones de pesetas.
Si el gasto es de 200 millones de pesetas no podemos
utilizar la recta de regresión puesto que el valor 200
esta fuera del recorrido del gasto en publicidad. Si
sustituimos nos da un valor de 76204 millones de
pesetas, pues las rectas sólo son válidas dentro del
rango o para valores próximos a los extremos del
recorrido.

33. d) Para solucionar este apartado calculamos el
coeficiente de correlación ordinal de Spearman.
El coeficiente de Spearman consiste en calcular
el coeficiente de correlación lineal de los datos
transformados a través de la función rango.
Y 10 15 20 22 30 32
X 16 32 48 56 64 80
Rang Y 1 2 3 4 5 6
Rang X 1 2 3 4 5 6
dᵢ 0 0 0 0 0 0
D²ᵢ 0 0 0 0 0 0

34. El coeficiente de Spearman cuando no existen
empates en los rangos, como ocurre en estos
datos, tiene la siguiente expresión:
En este caso es 1 por tanto existe
correlación ordinal positiva y perfecta , es decir a
mayor gasto en publicidad mayor volumen de
ventas.
Podemos observar que la correlación no es
perfecta y sin embargo la correlación ordinaria si
lo es
nn
d
r
n
i i
s
−
−=
∑=
3
1
2
6
1
sr