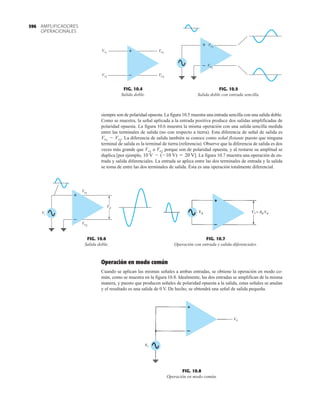
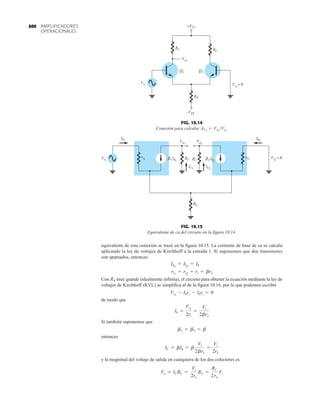
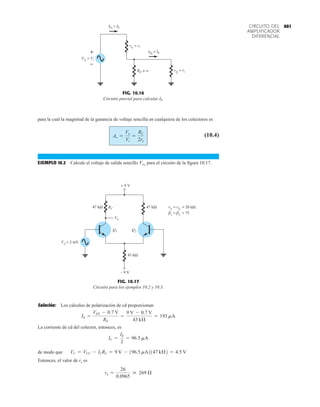
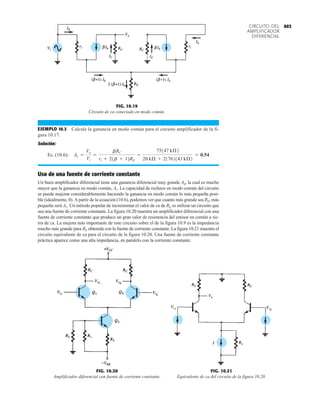
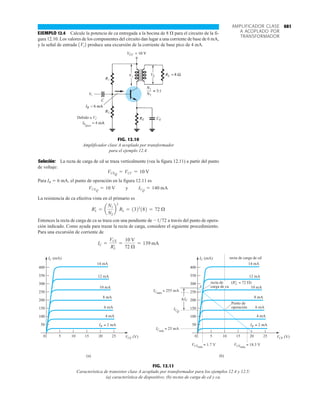
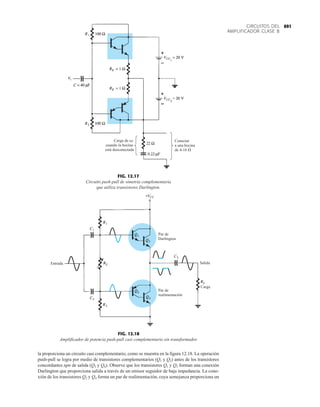
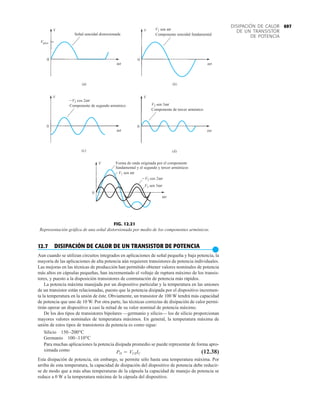
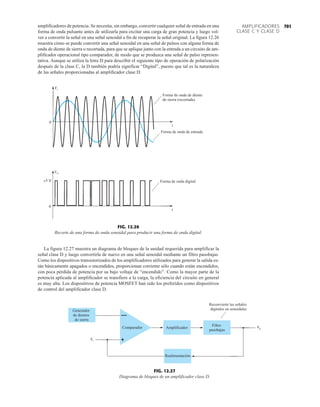
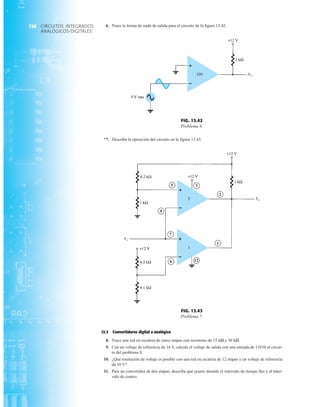
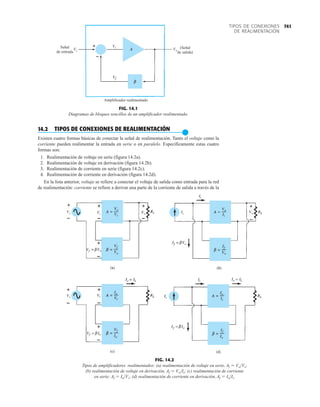
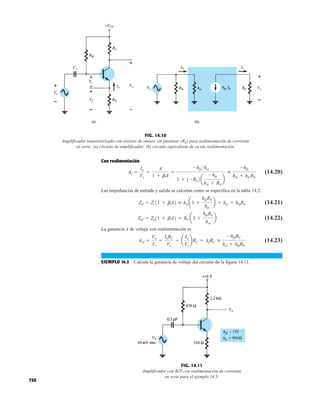
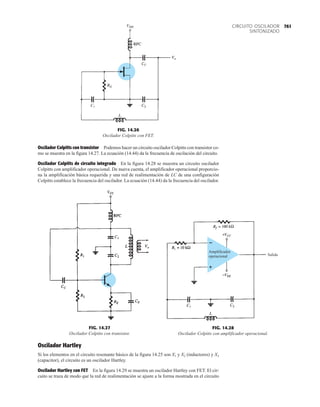
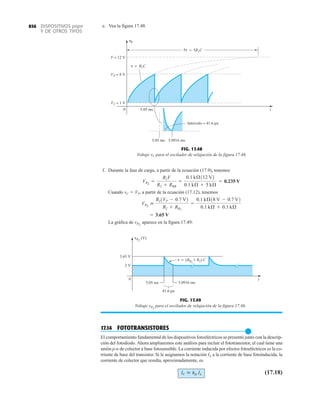
El documento describe la décima edición del libro de texto "Electrónica: teoría de circuitos y dispositivos electrónicos" de Boylestad y Nashelsky. El libro cubre una amplia gama de temas relacionados con los circuitos y dispositivos electrónicos, incluidos los diodos, transistores bipolares y de efecto de campo, amplificadores operacionales y de potencia, circuitos integrados analógicos y digitales, realimentación y osciladores. El objetivo del libro es proporcionar una comprensión completa y actualizada de












































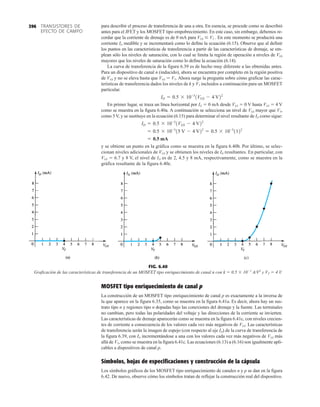
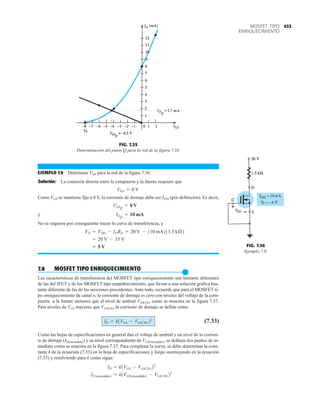
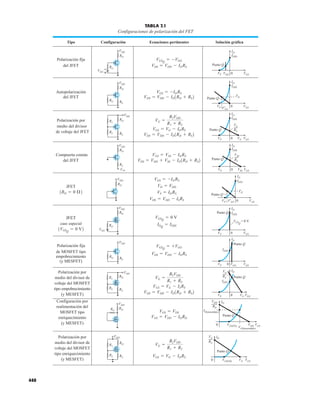
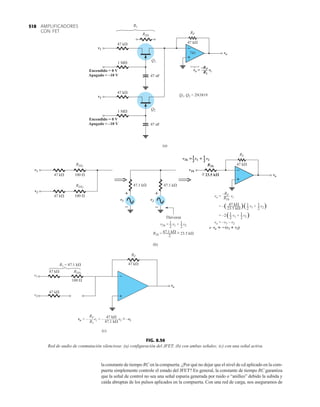
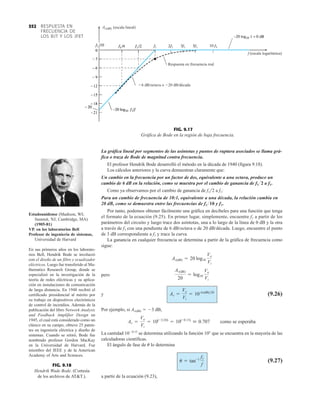
![DIODOS
SEMICONDUCTORES
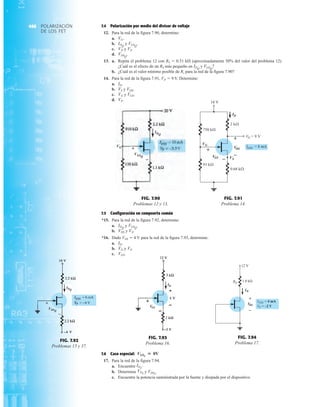
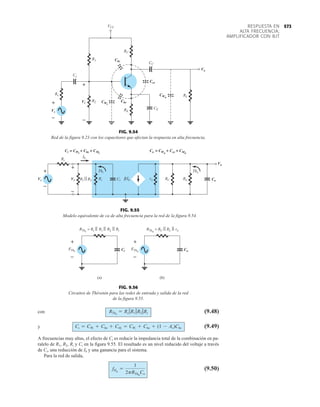
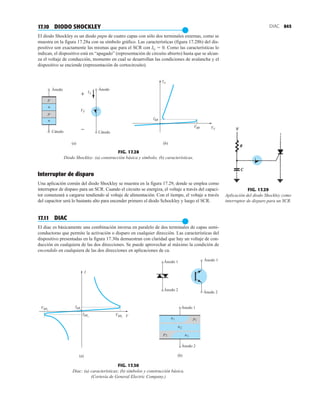
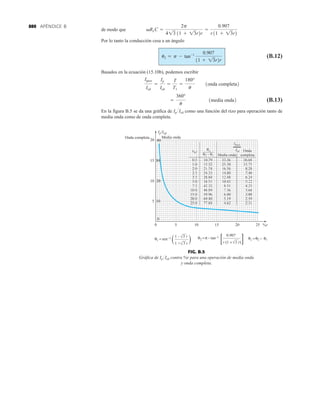
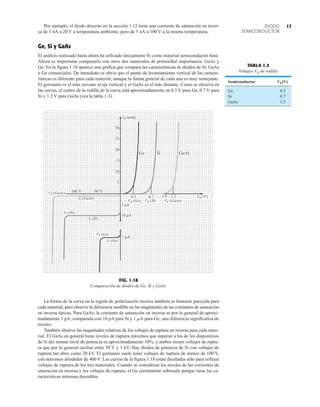
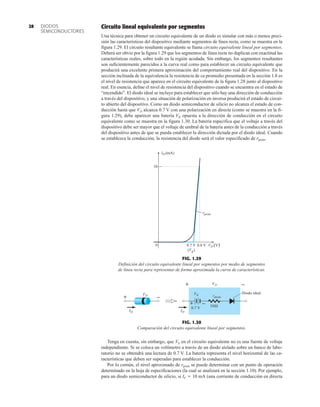
32 1.12 HOJAS DE ESPECIFICACIONES DE DIODOS
●
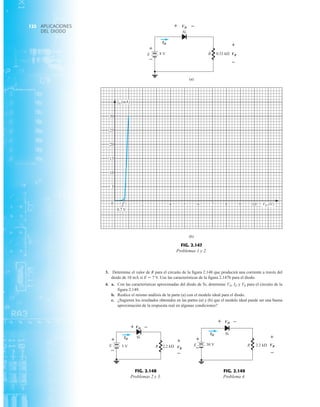
Normalmente, el fabricante proporciona datos sobre dispositivos semiconductores específicos
en una de dos formas. Con más frecuencia, dan una descripción muy breve, tal vez limitada a
una página. En otras ocasiones proporcionan un examen completo de las características median-
te gráficas, material gráfico, tablas, etc. En uno u otro caso, son piezas con datos específicos que
se deben incluir para el uso apropiado del dispositivo. Incluyen:
1. El voltaje en directa VF (a una corriente y temperatura especificadas)
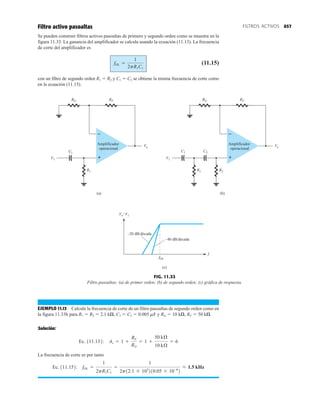
2. La corriente máxima en directa IF (a una temperatura especificada)
3. La corriente de saturación en inversa IR (a un voltaje y temperatura especificados)
4. El valor nominal de voltaje inverso [PIV, PRV, o V(BR), donde BR proviene del término
“breakdown” (ruptura) (a una temperatura especificada)]
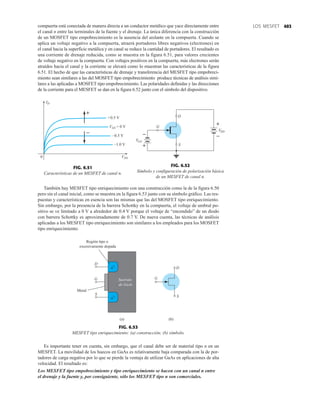
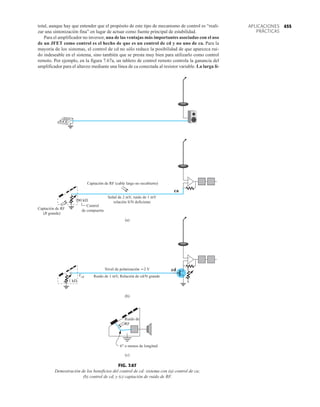
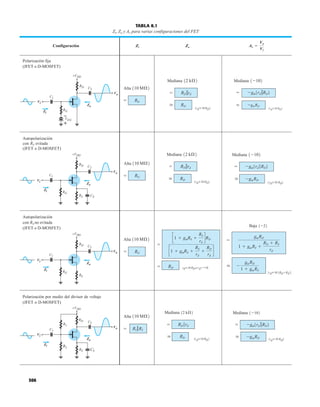
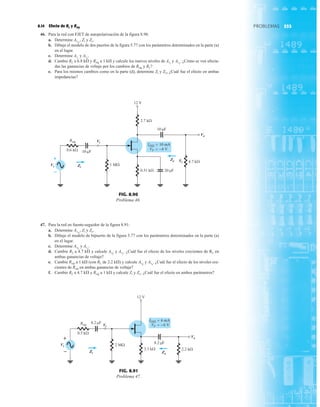
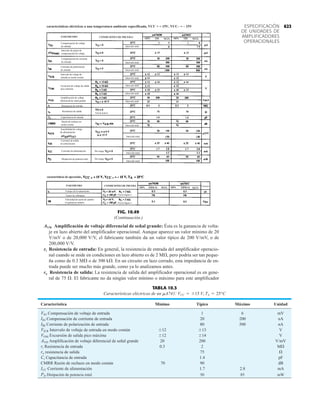
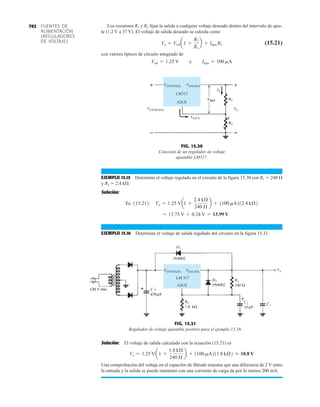
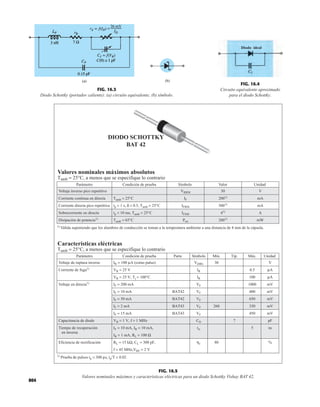
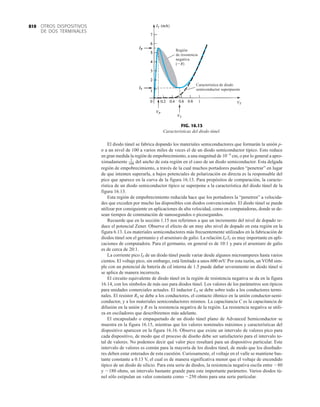
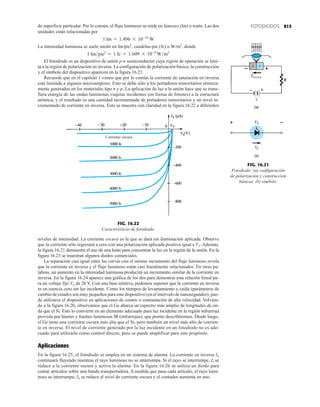
DIODO PLANO DE SILICIO DIFUSO
CANTIDADES NOMINALES MÁXIMAS ABSOLUTAS (Nota 1)
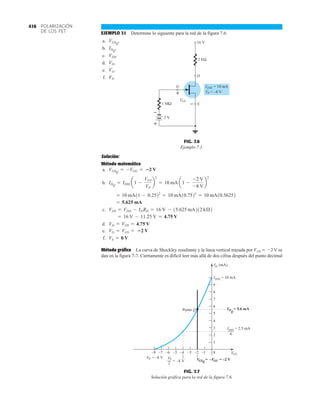
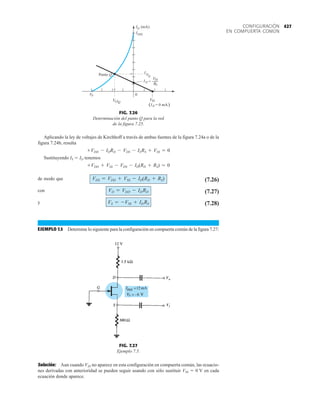
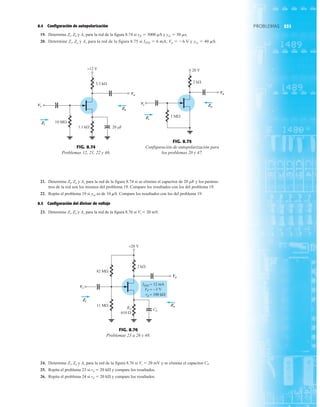
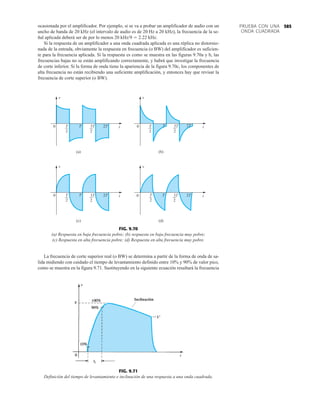
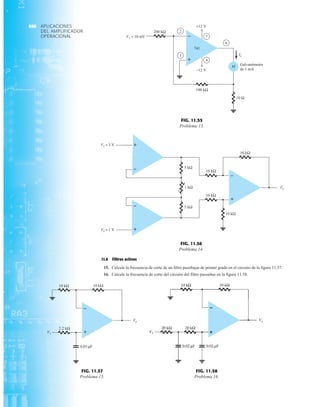
• BV . . . 125 V (MIN) @ 100 mA (BAY73)
Temperaturas
Intervalo de temperatura de almacenamiento
Temperatura máxima de operación en la unión
Temperatura en las terminales de conexión
Disipación de potencia (Nota 2)
Disipación de potencia nominal máxima total a 25°C
de temperatura ambiente
Factor de reducción de potencia lineal (a partir de 25°C)
Voltajes y corrientes nominales máximos
Voltaje en inversa de trabajo BAY73 100 V
–65°C a +200°C
+175°C
+260°C
500 mW
3.33 mW/°C
WIV
IF
Corriente rectificada promedio
Corriente en directa continua
Corriente directa repetitiva pico
200 mA
500 mA
600 mA
IO
if
if sobrecorriente Sobrecorriente directa pico
Ancho de pulso 1 s
Ancho de pulso 1 s
1.0 A
4.0 A
CARACTERÍSTICAS ELÉCTRICAS (Temperatura ambiente de 25°C a menos que se indique lo contrario)
SÍMBOLO CARACTERÍSTICA UNIDADES CONDICIONES DE PRUEBA
Voltaje en directa
Corriente en inversa
Voltaje de ruptura
Capacitancia
Tiempo de recuperación
en inversa
NOTAS:
1 Estas capacidades son valores límite sobre los cuales la funcionalidad del diodo puede verse afectada.
2 Éstos son límites de estado constante. Se deberá consultar al fabricante sobre aplicaciones que impliquen pulsos u operación de trabajo ligero.
ESQUEMA DEL DO35
NOTAS
Cables de acero cobrizados, estañados
Cables dorados disponibles
Cápsula de vidrio herméticamente sellada
El peso de la cápsula es de 0.14 gramos
A
B
C
D
E
F
G
BV
C
trr
IR
VF
H
BAY73
MÍN MÁX
V
V
V
V
V
V
nA
A
nA
nA
V
pF
s
IF 200 mA
IF 100 mA
IF 10 mA
IF 10 mA
IF 10 mA
IF 10 mA
VR 20 V, TA 125°C
VR 100V, TA 125°C
VR 20 V, TA 25°C
VR 100 V, TA 25°C
IR 100 A
VR 0, f 1.0 MHz
IF 10 mA, VR 35 V
RL 1.0 a 100 k
CL 10 pF, JAN 256
1.00
0.94
0.88
0.80
0.75
0.68
500
1.0
0.2
0.5
5.0
3.0
0.85
0.81
0.78
0.69
0.67
0.60
125
MÍN
DIÁ
DIÁ
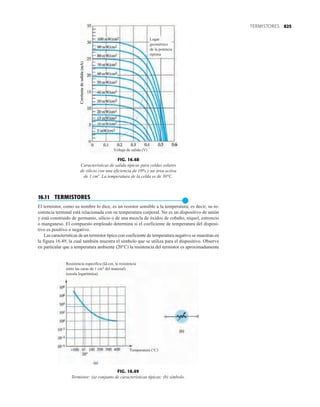
FIG. 1.36
Características eléctricas de un diodo de fugas escasas y alto voltaje.](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-51-320.jpg)
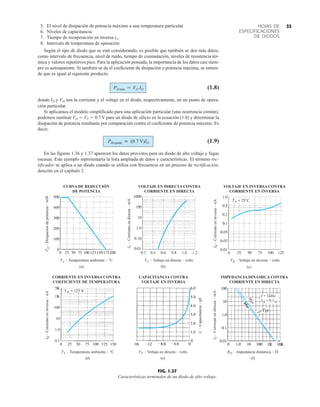









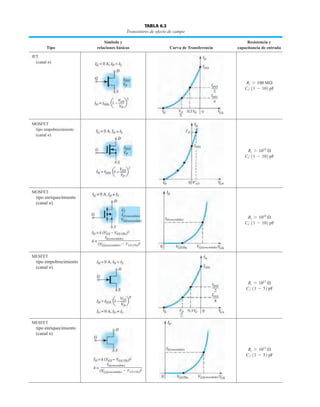
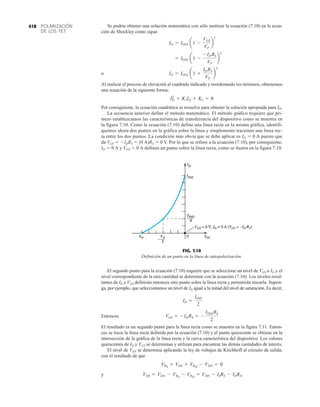
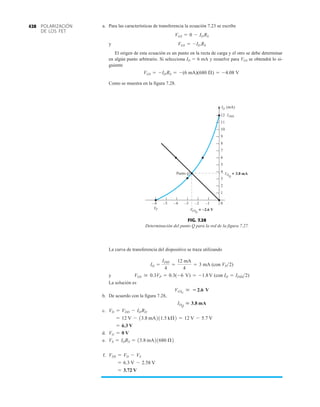
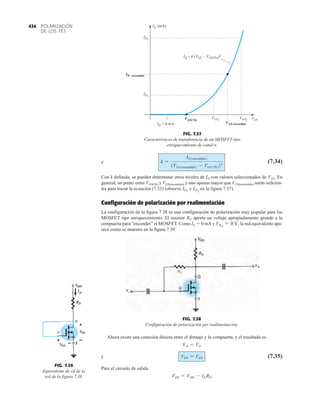
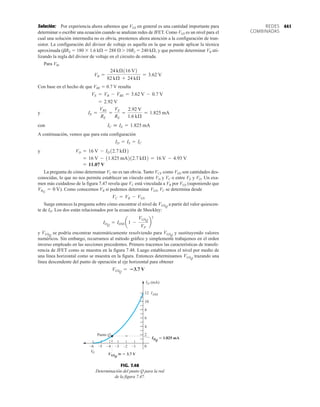
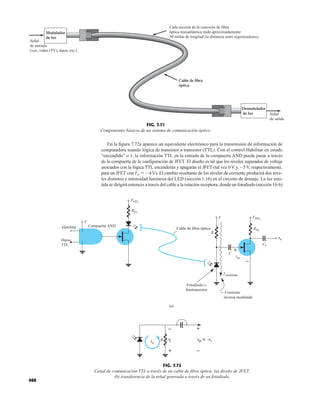
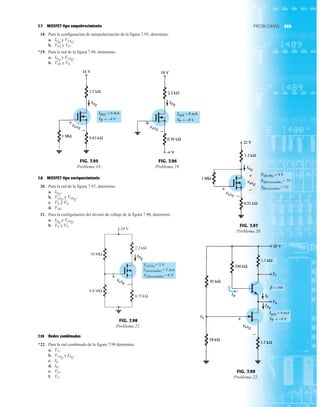
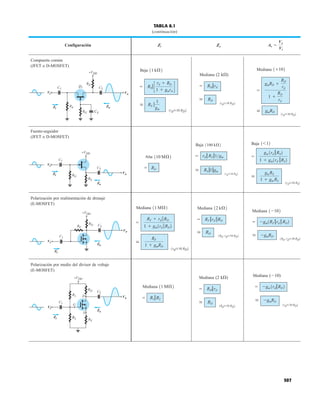
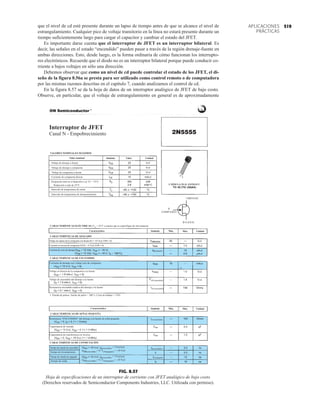
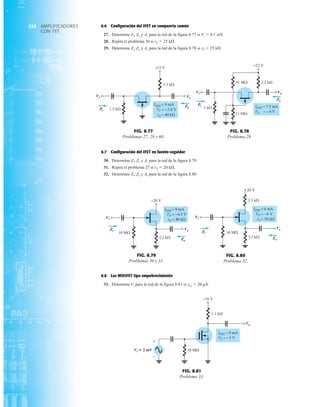
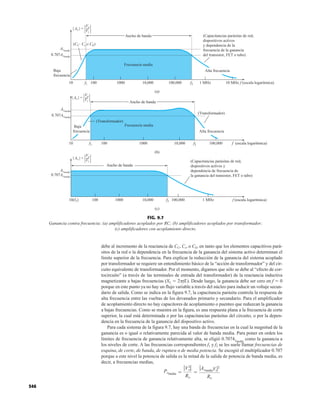
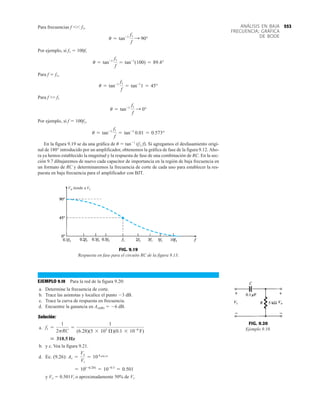
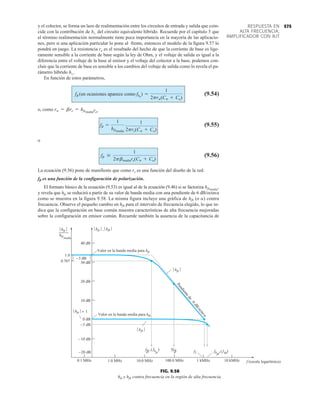
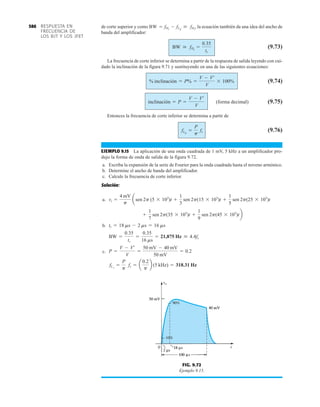
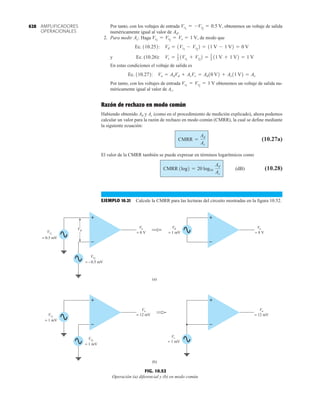
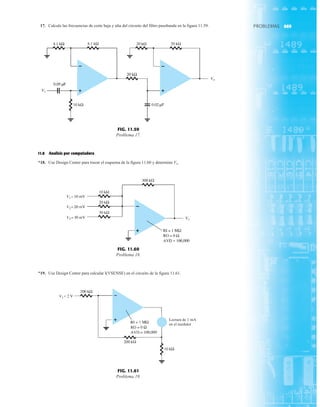
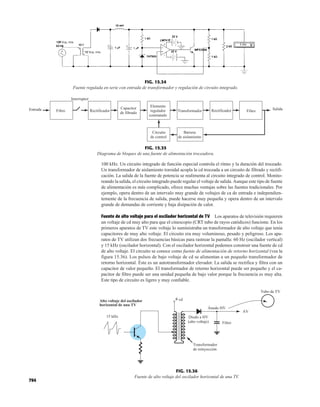
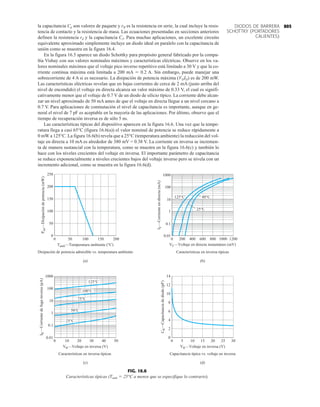
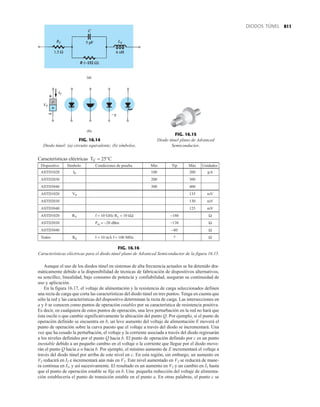
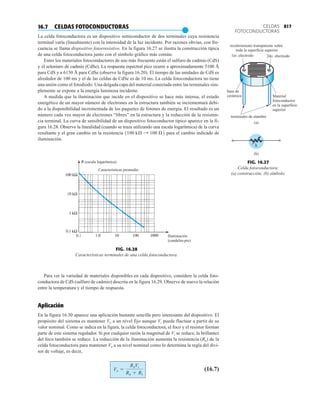
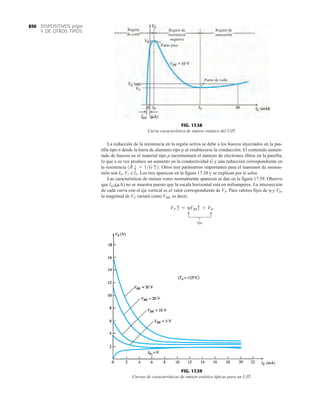
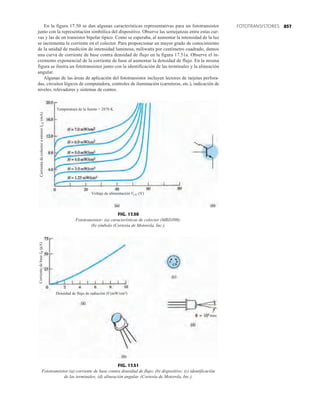
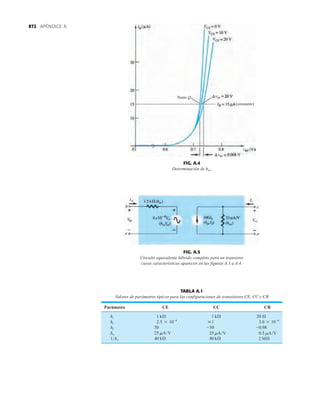
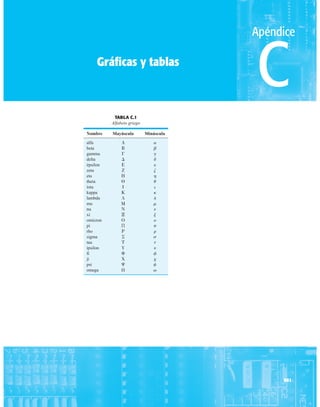
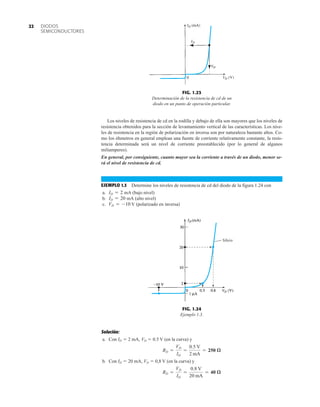
![debe ser suficiente para permitir que su nivel se compare entre dispositivos similares. La figura
1.53f es una gráfica normalizada de la intensidad luminosa relativa contra la corriente en direc-
ta. El término normalizada se utiliza con frecuencia en gráficas para comparar la respuesta con
un nivel particular.
Una gráfica normalizada es aquella en la que una variable de interés se grafica con un nivel
específico definido como valor de referencia con una magnitud de uno.
En la figura 1.53f el nivel normalizado se considera como IF 10 mA. Observe que la inten-
sidad luminosa es una a IF 10 mA. La gráfica revela de inmediato que la intensidad de la luz
casi se duplica con una corriente de 15 mA y es casi tres veces la corriente de 30 mA. Es impor-
tante por consiguiente señalar que:
la intensidad luminosa de un LED se incrementará con la corriente en directa hasta que se
alcanza un punto de saturación donde cualquier incremento adicional de la corriente no in-
crementa de forma efectiva el nivel de iluminación.
Cantidades nominales máximas absolutas a TA 25°C
Rojo 4160 de
Parámetro alta eficiencia Unidades
Disipación de potencia 120 mW
Corriente en directa promedio 20[1] mA
Corriente en directa pico 60 mA
Intervalo de temperatura de operación –55°C a 100°C
y almacenaje
Temperatura de soldadura de plomo 230°C para 3 s
(11.6 mm (0.063 pulg) del cuerpo
NOTA: Se reduce a partir de 50°C con 0.2 mV/°C
Características eléctricas/ópticas a TA 25°C
Rojo 4160 de
alta eficiencia
Símbolo Descripción Mín. Típ. Máx. Unidades Condiciones de prueba
IF 10 mA
IV Intensidad luminosa axial 1.0 3.0 mcd
2u1/2 Incluido el ángulo entre 80 grados Nota 1
puntos de mediana
intensidad luminosa
pico Longitud de onda pico 635 nm Medición en el pico
d Longitud de onda
dominante 628 nm Nota 2
s Velocidad de respuesta 90 ns
C Capacitancia 11 pF VF 0; ƒ 1 Mhz
uJC Resistencia térmica 120 °C/W Unión al conductor
cátodo a 0.79 mm
(0.031 pulg) del
cuerpo
VF Voltaje en directa 2.2 3.0 V IF 10 mA
BVR Voltaje de ruptura 5.0 V IR 100 A
en inversa
Eficacia luminosa 147 lm/W Nota 3
NOTAS:
1. u1/2 es el ángulo desplazado del eje al cual la intensidad luminosa es la mitad de la intensidad lumino-
sa axial.
2. La longitud de onda dominante 2d se deriva del diagrama de cromacidad CIE y representa la longitud
de onda única que define el color del dispositivo.
3. Intensidad radiante, Ie, en watts/esteradian, se puede encontrar con la ecuación Ie Iv/v, donde Iv es
la intensidad luminosa en candelas y v es la eficacia luminosa en lúmenes/watts.
m
(c)
(b)
(a)
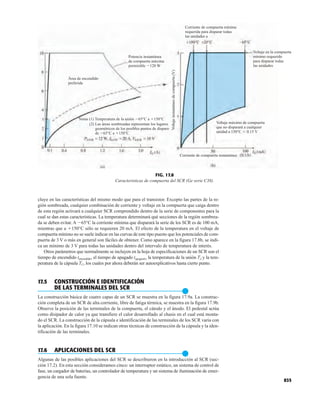
FIG. 1.53
Lámpara de estado sólido de alta eficiencia subminiatura Hewlett-Packard: (a) apariencia; (b) cantidades nominales máximas
absolutas: (c) características eléctricas ópticas; (d) intensidad relativa contra longitud de onda; (e) corriente en directa contra
voltaje en directa; (f) intensidad luminosa relativa contra corriente en directa; (g) eficiencia relativa contra corriente pico;
(h) intensidad luminosa contra desplazamiento angular (cortesía de Hewlett-Packard Corporation).
45](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-64-320.jpg)
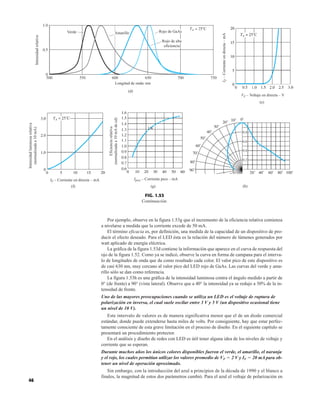



















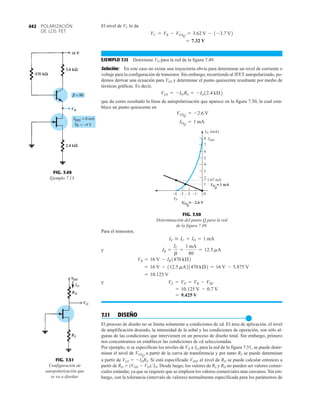
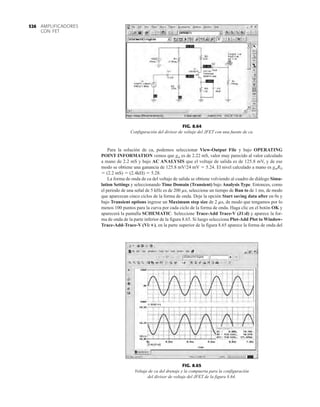
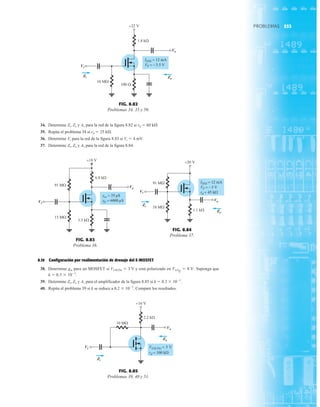
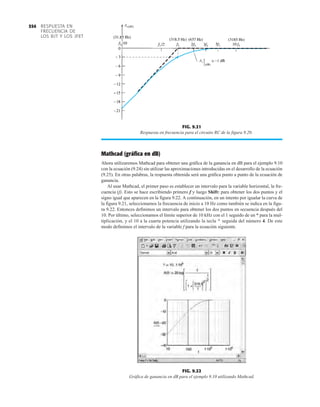
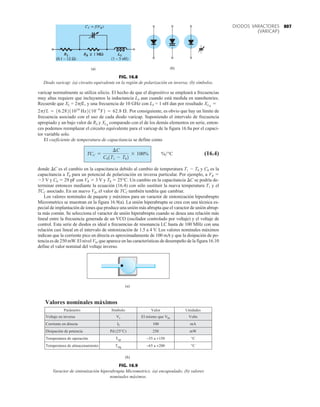
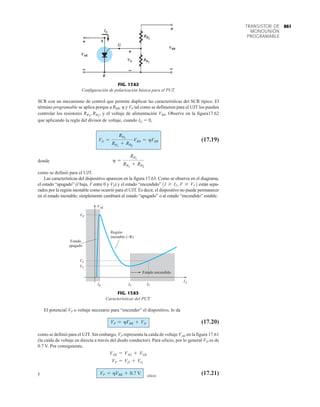
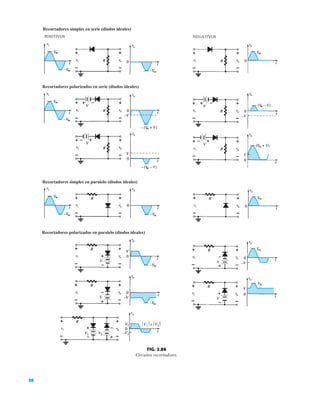
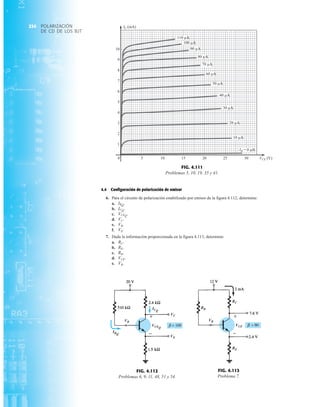
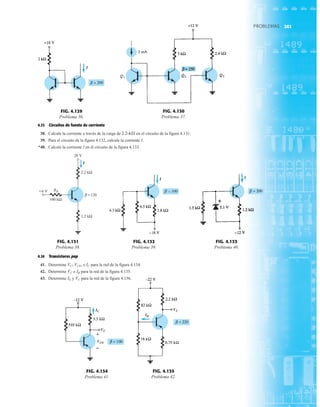
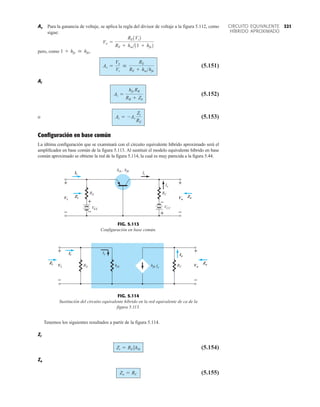
![69
CONFIGURACIONES
DE DIODOS EN SERIE
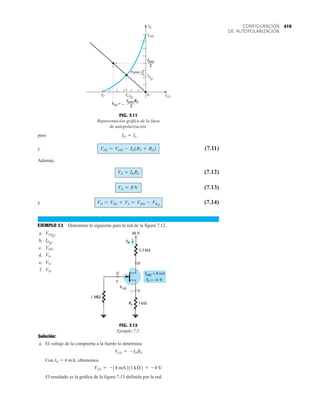
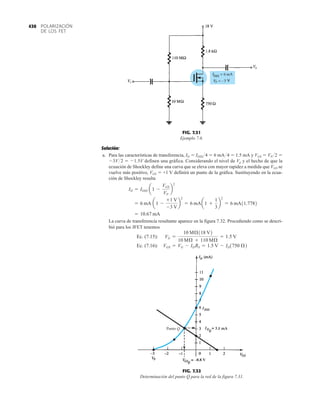
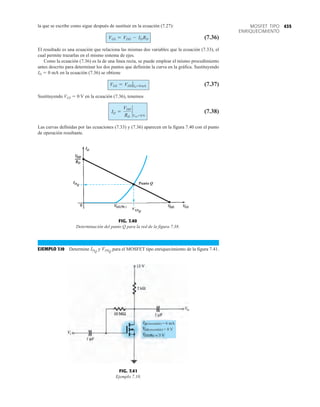
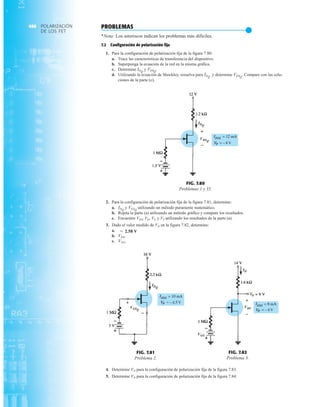
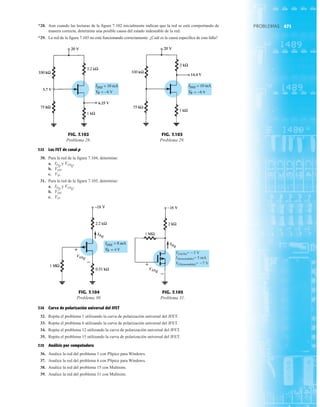
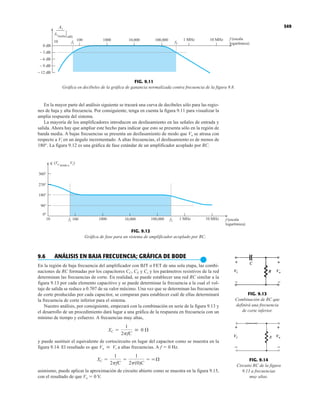
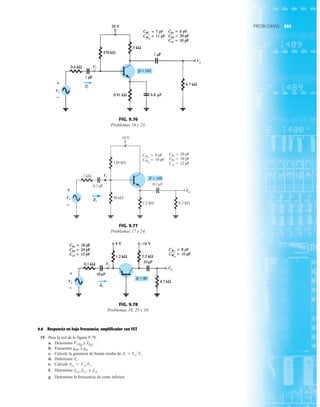
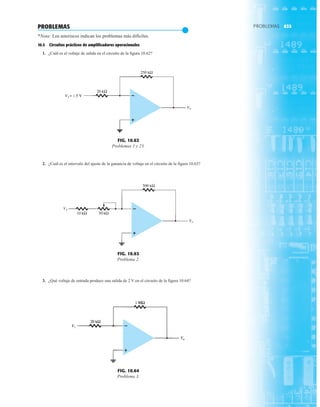
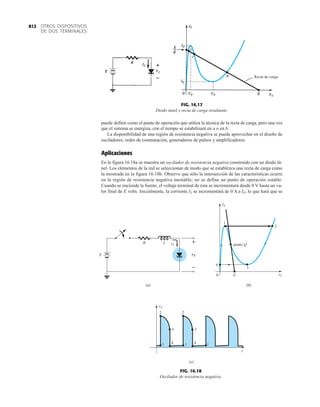
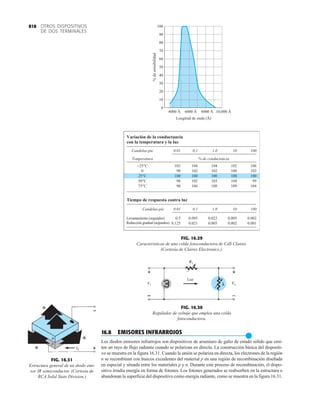
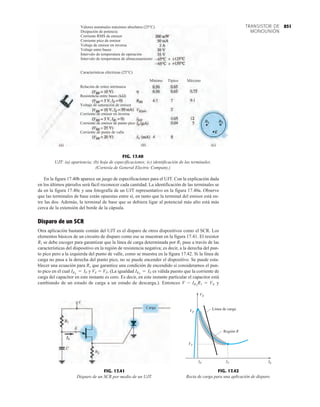
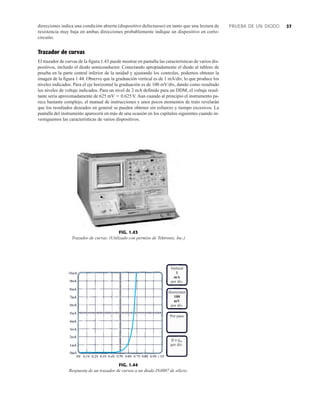
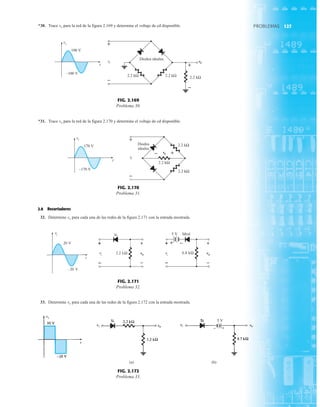
FIG. 2.17
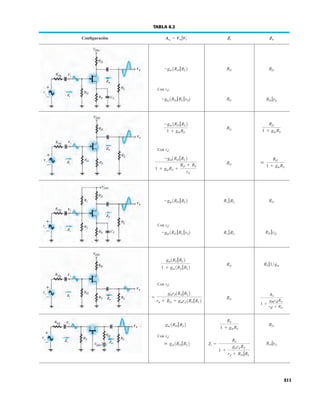
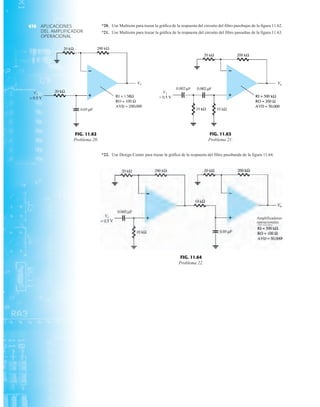
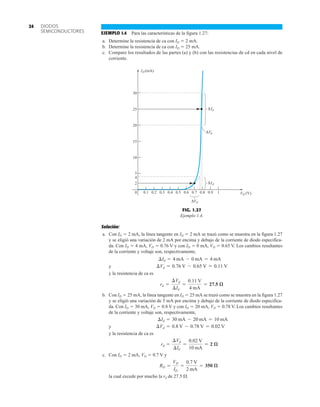
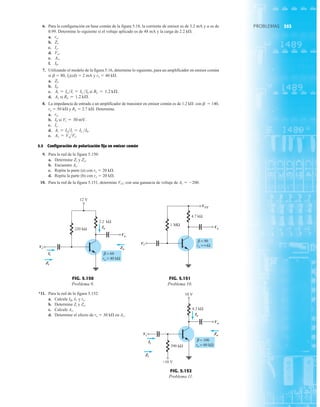
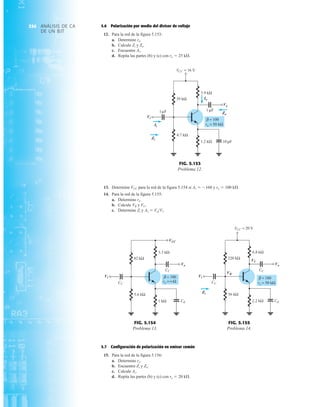
Punto de operación con E 0.5 V.
R
680 Ω
ID
I
2
K
V
1
K
V
12 V Vo
+
–
0.7 V 1.8 V
–
+
E
+ – + –
FIG. 2.20
Determinación de las cantidades
desconocidas del ejemplo 2.7.
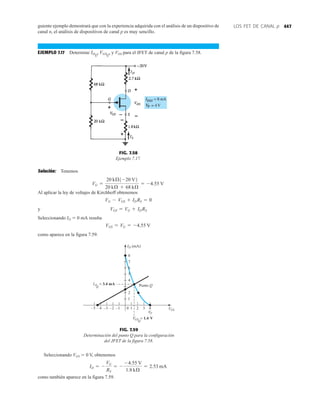
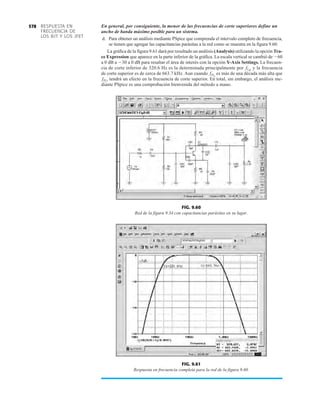
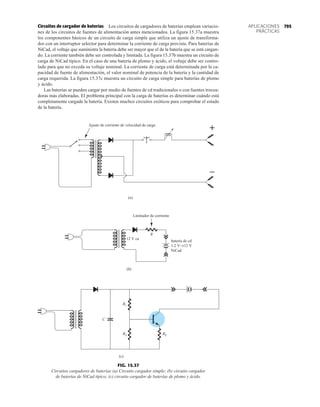
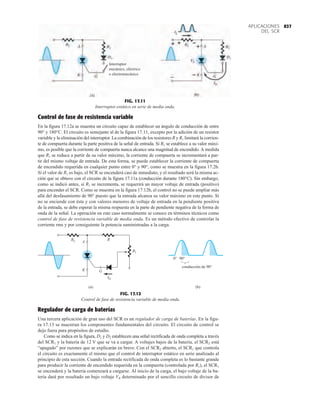
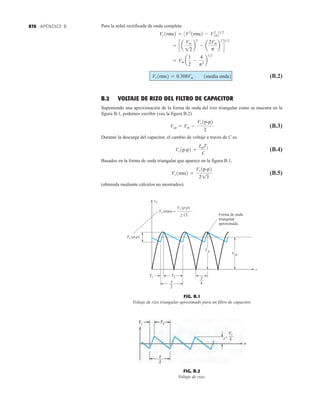
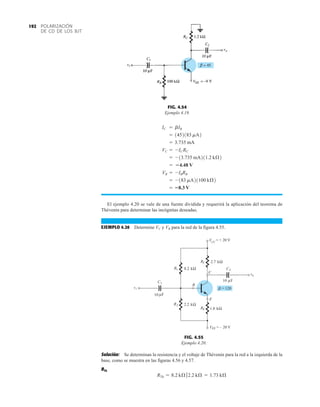
EJEMPLO 2.7 Determine Vo e ID para el circuito en serie de la figura 2.19.
Solución: Una forma igual de abordar el ejemplo 2.4 revelará que la dirección de la corriente
resultante coincide con la de las flechas de los símbolos de ambos diodos y se obtiene la red de
la figura 2.20 porque E 12 V (0.7 V 1.8 V [tabla 1.8]) 2.5 V. Observe la fuente de 12 V
vuelta a trazar y la polaridad de Vo a través del resistor de 680 . El voltaje resultante es
y ID = IR =
VR
R
=
Vo
R
=
9.5 V
680 Æ
= 13.97 mA
Vo = E - VK1
- VK2
= 12 V - 2.5 V = 9.5 V
FIG. 2.19
Circuito del ejemplo 2.7
rojo
ID
Vo
VD2
+ –
R
+20 V
kΩ
5.6
Si
ID
I
Si
Vo
FIG. 2.21
Circuito del ejemplo 2.8.
FIG. 2.22
Determinación del estado de los
diodos de la figura 2.21.
I
R 5.6 kΩ o
V
+
–
–
+
E
I = 0
+
–
FIG. 2.23
Sustitución del estado equivalente
por el diodo abierto.
FIG. 2.18
Determinación de ID, VR y Vo
para el circuito de la figura 2.16.
R
+0.5 V
–
+
VD
–
+
ID = 0 mA
VR = 0 V
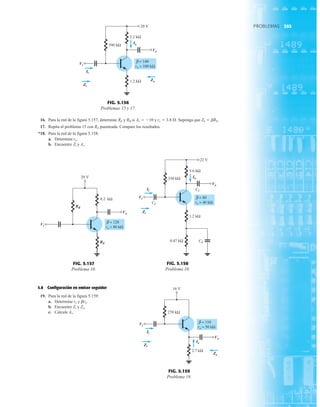
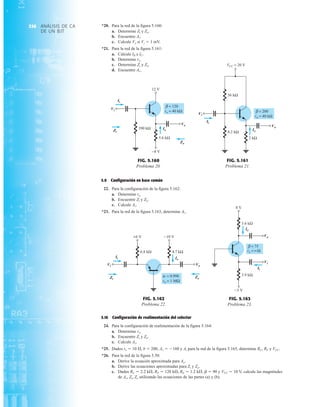
EJEMPLO 2.8 Determine ID, y Vo para el circuito de la figura 2.21.
Solución: Eliminar los diodos y determinar la dirección de la corriente resultante I da como resul-
tado el circuito de la figura 2.22. La dirección de la corriente en el diodo de silicio coincide pero
no en el de germanio. La combinación de un corto circuito en serie con un circuito abierto siem-
pre da por resultado un circuito abierto e ID 0 A, como se muestra en la figura 2.23.
VD2](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-88-320.jpg)







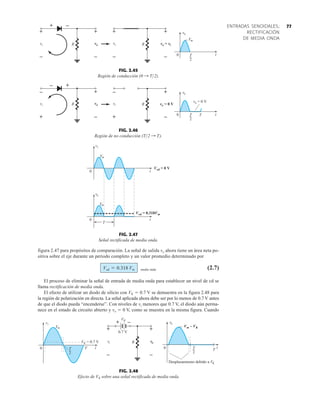

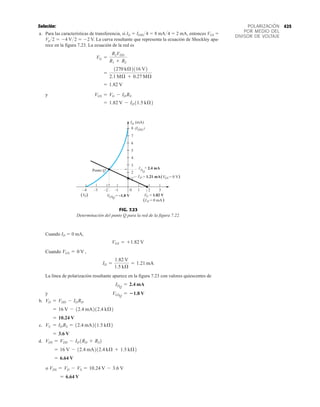
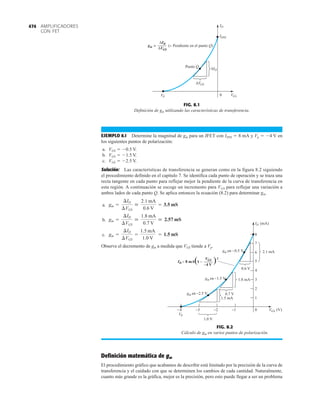
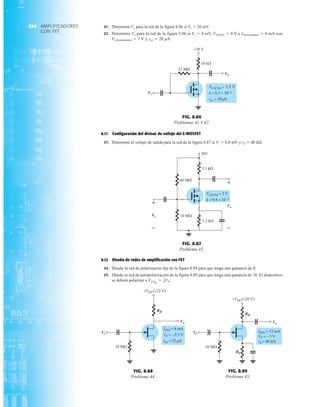
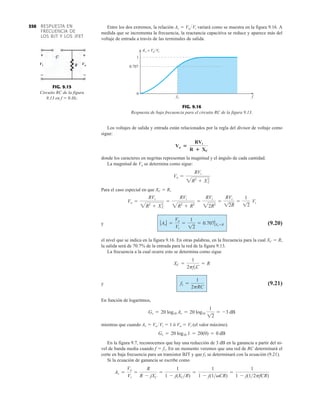
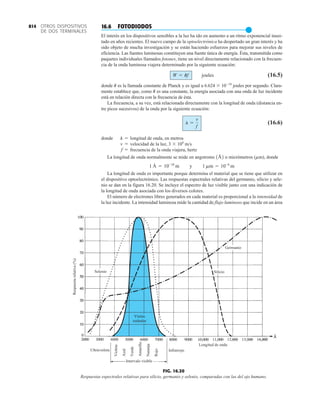
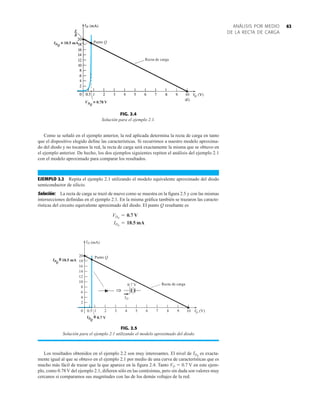
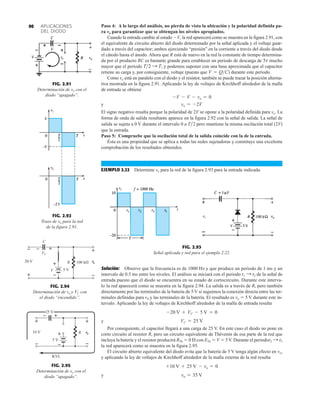
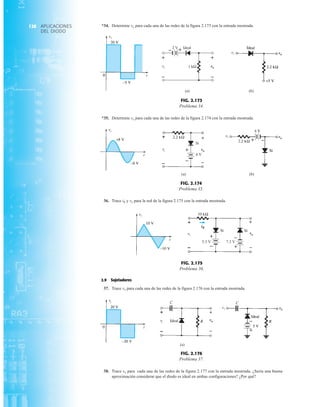
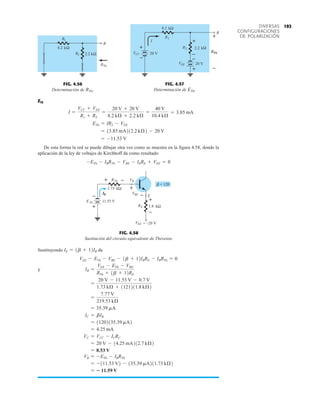
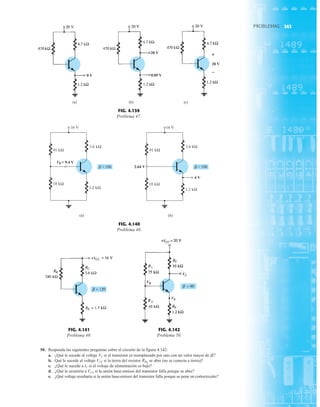
![79
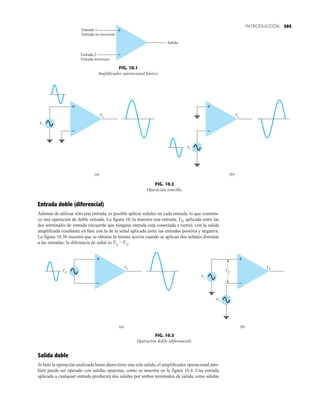
RECTIFICACIÓN DE
ONDA COMPLETA
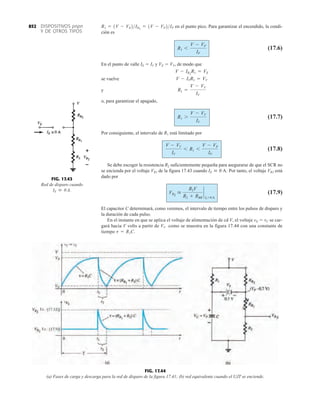
PIV (PRV)
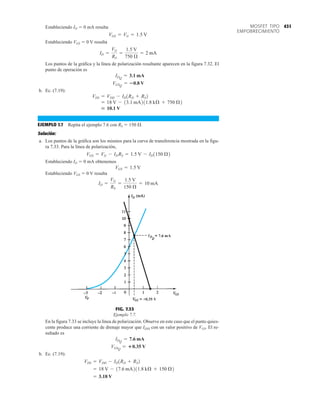
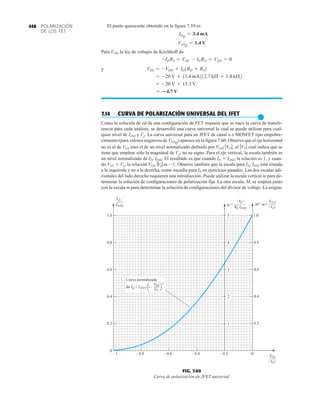
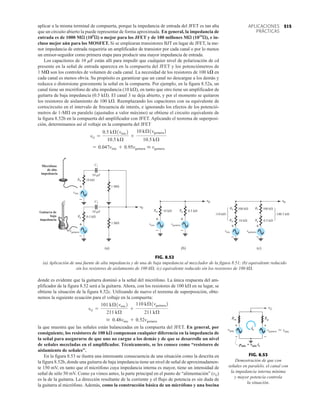
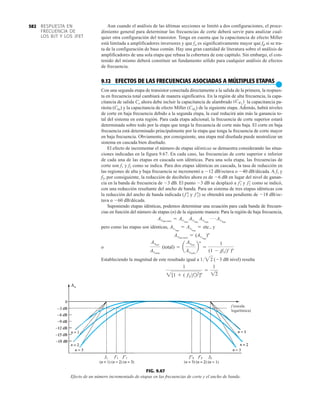
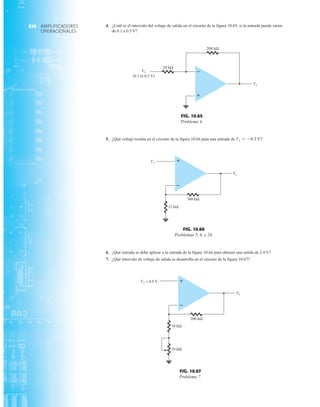
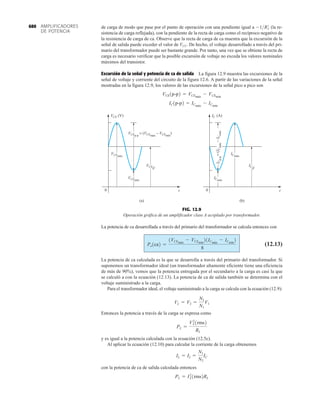
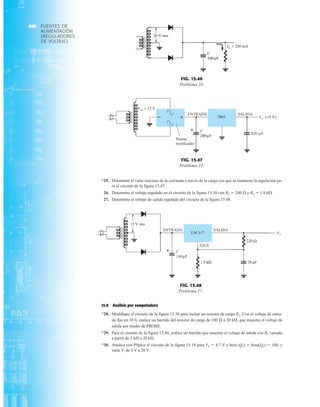
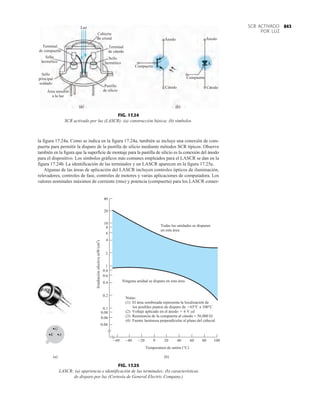
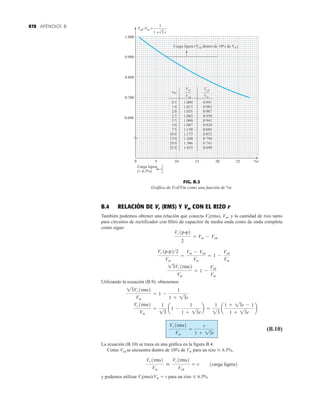
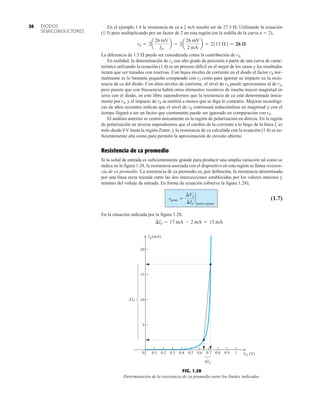
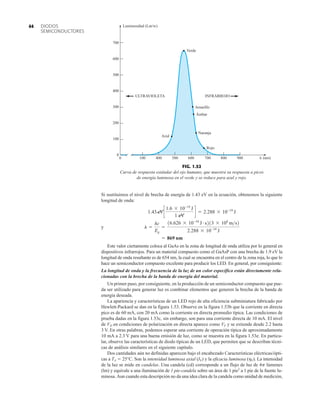
La capacidad de voltaje inverso pico (PIV) [o PRV (voltaje reverso pico )] del diodo es de primor-
dial importancia en el diseño de sistemas de rectificación. Recuerde que no se debe exceder el
valor nominal de voltaje en la región de polarización en inversa o el diodo entrará a la región de
avalancha Zener. El valor nominal de PIV requerido para el rectificador de media onda se deter-
mina con la figura 2.52, la cual muestra el diodo polarizado en inversa de la figura 2.44 con un
voltaje máximo aplicado. Aplicando la ley de voltajes de Kirchhoff, es obvio que el valor nominal
de PIV del diodo debe ser igual a o exceder el valor pico del voltaje aplicado. Por consiguiente,
(2.9)
PIV nominal G Vm Rectificador de media onda
R
+ + +
+ +
– – –
– –
ap.
ap.
enc.
enc.
o
v
i
v
+
–
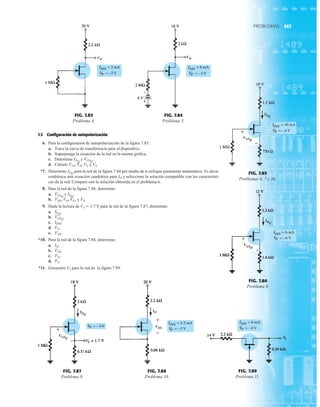
FIG. 2.54
Red de la figura 2.53 durante
el periodo del
voltaje de entrada vi.
0 : T2
FIG. 2.52
Determinación del valor nominal del PIV
requerida para el rectificador de media onda.
Vm R
V (PIV)
– +
I = 0
–
+
Vo = IR = (0)R = 0 V
–
+
FIG. 2.53
Rectificador de onda completa en configuración de puente.
T
T
2
i
v
0 R
+
–
o
v
i
v
+
–
D1
D3 D4
D2
t
Vm
FIG. 2.55
Ruta de conducción en la región positiva de vi.
R
+
–
o
v
i
v
– +
0 T
2
t
i
v
Vm
0 T
2
t
o
v
Vm
2.7 RECTIFICACIÓN DE ONDA COMPLETA
●
Rectificador de puente
El nivel de cd obtenido a partir de una entrada senoidal se puede mejorar 100% mediante un
proceso llamado rectificación de onda completa. La red más conocida para realizar tal función
aparece en la figura 2.53 con sus cuatro diodos en una configuración de puente. Durante el
periodo t 0 para la polaridad de la entrada es como se muestra en la figura 2.54. Las po-
laridades resultantes a través de los diodos ideales también se muestran en la figura 2.54 para
revelar que D2 y D3 están conduciendo, mientras que D1 y D4 están “apagados”. El resultado
neto es la configuración de la figura 2.55 con su corriente y polaridad indicadas a través de R.
Como los diodos son ideales, el voltaje de carga es vo vi, como se muestra en la misma fi-
gura.
T2](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-98-320.jpg)
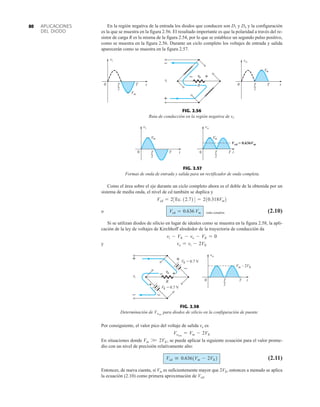


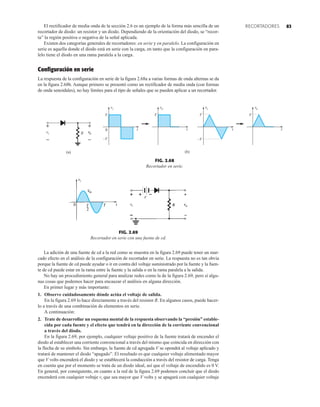

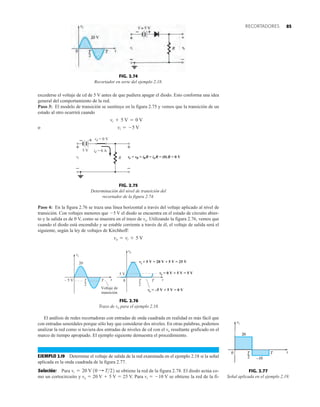




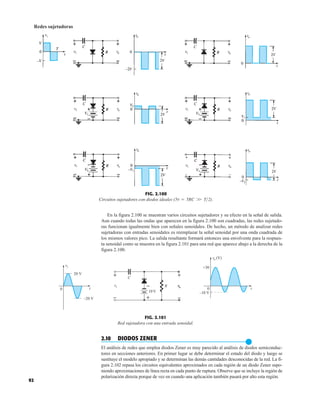






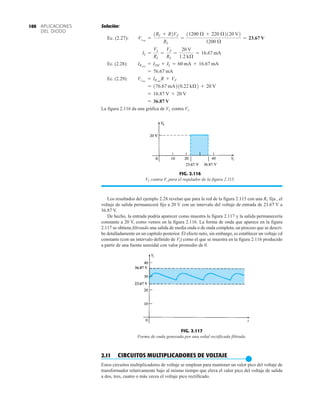





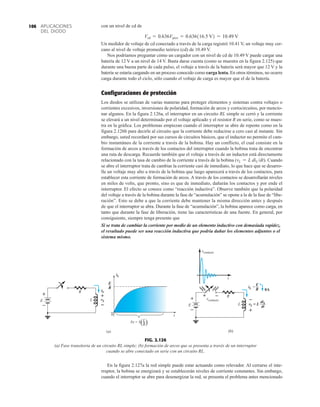

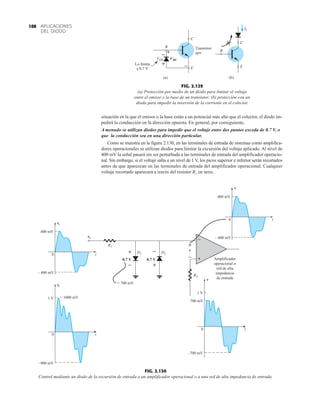




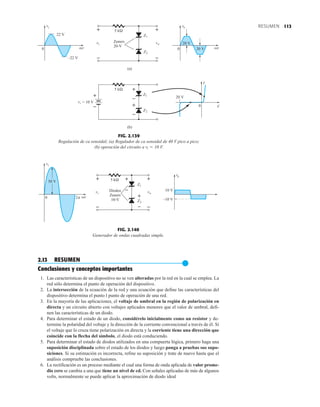












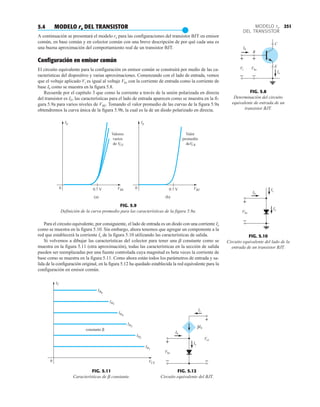
![133
OPERACIÓN
DEL TRANSISTOR
E
+ Portadores mayoritarios
VEE
B
Región de
empobrecimiento
+ –
+ –
+ +
+
+
+
+ + +
+ +
+
+
–
–
–
–
–
–
–
–
–
– –
–
p n
FIG. 3.3
Unión polarizada en directa de un transistor pnp.
–
+ +
+
+
++
+
+
+
+ – –
–
–
–
–
–
p
n
+
++ –
–
–
–
–
VCC
B
Región de
empobrecimiento
+ –
+ Portadores minoritarios
C
+ –
FIG. 3.4
Unión polarizada en inversa de un transistor pnp.
VCC
E
B
VEE
Región de
empobrecimiento
+ Portadores minoritarios
C
+ Portadores mayoritarios
IE
IB
IC
p p
n
+ – + –
FIG. 3.5
Flujo de portadores mayoritarios y minoritarios
de un transistor pnp.
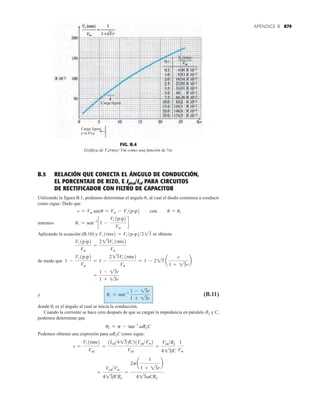
En la figura 3.5 se aplicaron ambos potenciales de polarización a un transistor pnp, con los
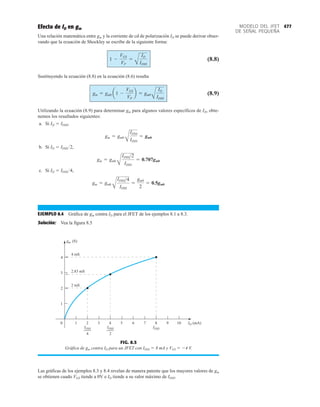
flujos de portadores mayoritarios y minoritarios resultantes indicados. Observe en la figura 3.5
los anchos de las regiones de empobrecimiento donde se ve con claridad cuál unión es polarizada
en directa y cual lo está polarizada en inversa. Como se indica en la figura 3.5, una gran canti-
dad de portadores mayoritarios se difundirá a través de la unión p–n polarizada en directa hacia
el material tipo n. La pregunta es entonces si estos portadores contribuirán directamente con la
corriente de base IB o si pasarán directamente al material tipo p. Como el material tipo n empa-
redado es muy delgado y su conductividad es baja, un número muy pequeño de estos portado-
res tomarán esta ruta de alta resistencia hacia la base. La magnitud de la corriente de base es por
lo general del orden de microamperes, en comparación con los miliamperes de las corrientes del
emisor y el colector. El mayor número de estos portadores mayoritarios se difundirá a través
de la unión polarizada en inversa hacia el material tipo n conectado al colector como se indica
en la figura 3.5. La razón de la facilidad relativa con que los portadores mayoritarios pueden
atravesar la unión polarizada en inversa es fácil de entender si consideramos que en el caso del
diodo polarizado en inversa los portadores mayoritarios inyectados aparecerán como portadores
minoritarios en el material tipo p. En otras palabras, ha habido una inyección de portadores mi-
noritarios en el material tipo n de la región de la base. Si se combina esto con el hecho de que
todos los portadores minoritarios de la región de empobrecimiento atravesarán la unión polari-
zada en inversa de un diodo explica el flujo indicado en la figura 3.5.
Aplicando la ley de las corrientes de Kirchhoff al transistor de la figura 3.5 como si fuera un
nodo único obtenemos
(3.1)
y hallamos que la corriente en el emisor es la suma de las corrientes en el colector y la base. La
corriente del colector, sin embargo, consta de dos componentes, los portadores mayoritarios y los
minoritarios como se indica en la figura 3.5. El componente de corriente de portadores minorita-
rios se llama corriente de fuga y se le da el símbolo ICO [corriente IC con el emisor abierto Abier-
to (Open)]. La corriente del colector, por consiguiente, está determinada en su totalidad por
(3.2)
IC = ICmayoritarios + ICOminoritarios
IE = IC + IB](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-152-320.jpg)



















![159
PROBLEMAS
11. Utilizando las características de la figura 3.7 determine VBE con IE 5 mA y VCB 1.10 y 20 V. ¿Es
razonable suponer de una forma aproximada que VCB tiene sólo un efecto leve en la relación entre
VBE e IE?
12. a. Determine la resistencia de ca promedio para las características de la figura 3.10b.
b. Para redes en las que la magnitud de los elementos resistivos es por lo general de kilohms, ¿es vá-
lida la aproximación de la figura 3.10c [basada en los resultados de la parte (a)]?
13. a. Con las características de la figura 3.8, determine la corriente en el colector si IE 4.5 mA y
VCB 4 V.
b. Repita la parte (a) con IE 4.5 mA y VCB 16 V.
c. ¿Cómo han afectado los cambios en VCB el nivel resultante de IC?
d. De una forma aproximada, ¿Cómo se relacionan IE e IC con base en los resultados anteriores?
14. a. Utilizando las características de las figuras 3.7 y 3.8, determine IC si VCB 10 V y VBE 800 mV.
b. Determine VBE si IC 5 mA y VCB 10 V.
c. Repita la parte (b) usando las características de la figura 3.10b.
d. Repita la parte (b) usando las características de la figura 3.10c.
e. Compare las soluciones de VBE para las partes (b) a (d). ¿Se puede ignorar la diferencia si por lo
general se presentan niveles de voltaje de más de algunos volts?
15. a. Dada acd de 0.998, determine IC si IE 4 mA.
b. Determine acd si IE 28 mA e IB 20 mA.
c. Encuentre IE si IB 40 mA y acd 0.98.
16. De memoria, trace la configuración de un transistor BJT en base común (npn y pnp) e indique la po-
laridad de la polarización aplicada y las direcciones de la corriente resultante.
3.5 Acción amplificadora del transistor
17. Calcule la ganancia de voltaje (Av VLVi) para la red de la figura 3.8 si Vi 500 mV y R 1 kÆ.
(Los demás valores del circuito no cambian.)
18. Calcule la ganancia de voltaje (Av VLVi) para la red de la figura 3.12 si la resistencia interna de la
fuente es de 100 Æ en serie con Vi.
3.6 Configuración en emisor común
19. Defina ICBO e ICEO. ¿En qué son diferentes? ¿Cómo están relacionadas? ¿Son en general de magnitud
parecida?
20. Utilizando las características de la figura 3.14:
a. Determine el valor de IC correspondiente a VBE +750 mV y VCE +5 V.
b. Determine el valor de VCE y VBE correspondiente a IC 3 mA e IB 30 mA.
*21. a. Para las características en emisor común de la figura 3.14, determine la beta de cd en un punto de
operación de VCE +8 V e IC 2 mA.
b. Determine el valor de a correspondiente a este punto de operación.
c. En VCE +8 V, determine el valor correspondiente de ICEO.
d. Calcule el valor aproximado de ICBO con el valor de beta de cd obtenido en la parte (a).
*22. a. Utilizando las características de la figura 3.14a, determine ICEO en VCE 10 V.
b. Determine bcd en IB 10 mA y VCE 10 V.
c. Utilizando la bcd determinada en la parte (b) calcule ICBO.
23. a. Con base en las características de la figura 3.14a, determine bcd con IB 80 mA y VCE 5 V.
b. Repita la parte (a) en IB 5 mA y VCE 15 V.
c. Repita la parte (a) en IB 30 mA y VCE 10 V.
d. Revisando los resultados de las partes (a) a (c), ¿cambia el valor de bcd de punto a punto sobre la
curva de las características? ¿Dónde se encontraron los valores más altos? ¿Puede llegar a algu-
na conclusión general sobre el valor de bcd con las características de la figura 3.14a?
*24. a. Utilizando las características de la figura 3.14a, determine bca en IB 80 mA y VCE 5 V.
b. Repita la parte (a) en IB 5 mA y VCE 15 V.
c. Repita la parte (a) en IB 30 mA y VCE 10 V.
d. Revisando los resultados de las partes (a) a (c), ¿cambia el valor de bca de un punto a otro sobre
la curva de las características? ¿Dónde se localizan los valores más altos? ¿Puede llegar a alguna
conclusión general sobre el valor de bca sobre un conjunto de las características del colector?
e. Los puntos seleccionados en este ejercicio son los mismos que se emplearon en el problema 23.
Si éste se efectuó, compare los niveles de bcd y bca en cada punto y comente sobre la tendencia de
la magnitud para cada cantidad.
25. Utilizando las características de la figura 3.14a, determine bcd en IB 25 µA y VCE 10 V. Luego
calcule acd y el nivel resultante de IE. (Use el nivel de IC determinado por IC bcdIB.)](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-178-320.jpg)



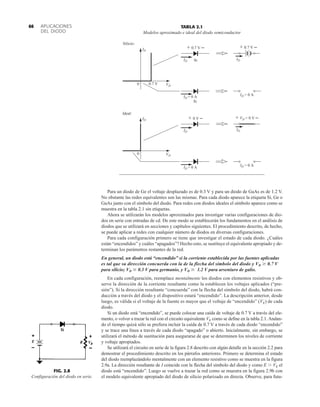
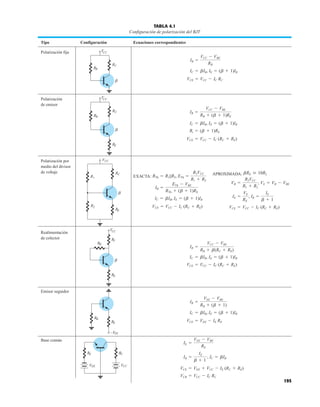
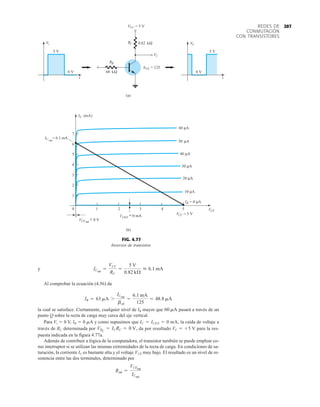
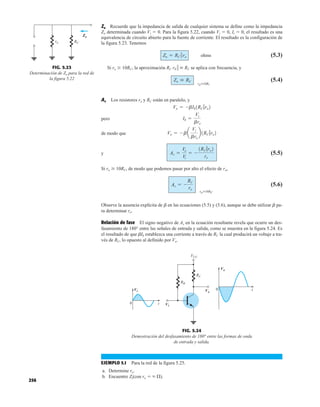
![163
PUNTO DE OPERACIÓN
5
IC máx
Saturación
IC (mA)
VCE
0
5
10
15
20
25
10 15
80 μA
60 μA
50 μA
40 μA
30 μA
20 μA
10 μA
Corte
VCEmáx
VCEsat
B
D
C
PC máx
70 μA
20 (V)
A
0 μA
IB =
FIG. 4.1
Varios puntos de operación dentro de los límites de operación de un transistor.
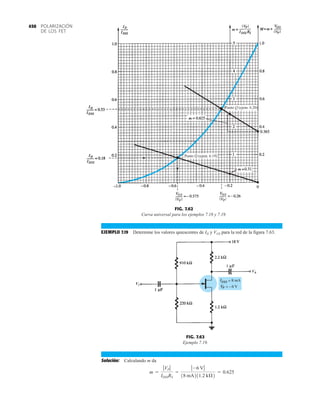
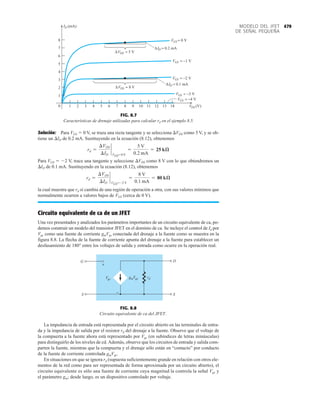
con rapidez en esta región. En general, es preferible operar donde la ganancia del dispositivo es
bastante constante (o lineal) para garantizar que la amplificación a lo largo de toda la excursión
de la señal de entrada sea la misma. El punto B es una región de más separación lineal, y por
consiguiente de más operación lineal, como se muestra en la figura 4.1. El punto D sitúa el pun-
to de operación cerca del nivel máximo de voltaje y potencia. El voltaje de salida excursiona en
la dirección positiva, y por lo tanto se limita si no se excede el voltaje máximo. Por consiguien-
te, parece que el punto B es el mejor punto de operación en función de ganancia lineal y máxi-
ma excursión posible de voltaje y de corriente. En realidad, ésta es la condición deseada para
amplificadores de señal pequeña (capítulo 5) aunque no necesariamente para amplificadores de
potencia, los cuales se considerarán en el capítulo 12. En este análisis nos concentraremos prin-
cipalmente en polarizar el transistor para operación de amplificación de señal pequeña.
Hay que considerar otro factor de polarización muy importante. Habiendo seleccionado y pola-
rizado el BJT en un punto de operación deseado, también debemos tomar en cuenta el efecto de
la temperatura. La temperatura cambia los parámetros del dispositivo al igual que la ganancia
de corriente del transistor y su corriente de fuga (ICEO). Las altas temperaturas incremen-
tan las corrientes de fuga en el dispositivo, y cambian por lo tanto las condiciones de operación
establecidas por la red de polarización. El resultado es que el diseño de la red también debe pro-
porcionar un grado de estabilidad de temperatura, de modo que los cambios ambientales produz-
can cambios mínimos en el punto de operación. Este mantenimiento del punto de operación puede
ser especificado por un factor de estabilidad S, el cual indica el grado de cambio del punto
de operación provocado por una variación de la temperatura. Es deseable un circuito altamente
estable, y se comparará la estabilidad de algunos circuitos de polarización básicos.
Para que el BJT se polarice en su región de operación lineal o activa lo siguiente debe ser cierto:
1. La unión base-emisor debe polarizarse en directa (voltaje más positivo en la región p),
con el voltaje de polarización en directa resultante de cerca de 0.6 a 0.7 V.
2. La unión base-colector debe polarizarse en inversa (más positivo en la región n), con el
voltaje de polarización en inversa de cualquier valor dentro de los límites del dispositivo.
[Observe que para la polarización en directa el voltaje a través de la unión p-n es p positivo, en
tanto que para la polarización en inversa es opuesto (inverso) con n positiva. Este énfasis en la
letra inicial deberá servir para memorizar la polaridad necesaria del voltaje.]
La operación en las regiones de corte, saturación y lineal de la característica BJT se da como
sigue:
1bca2](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-182-320.jpg)


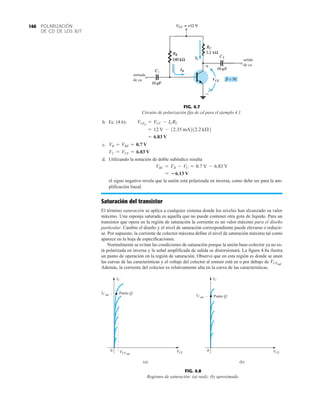

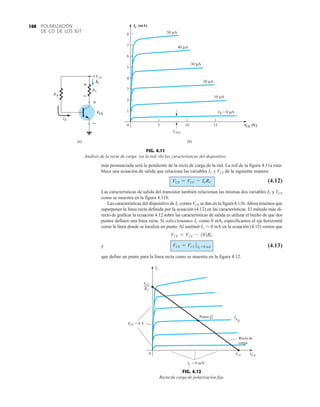


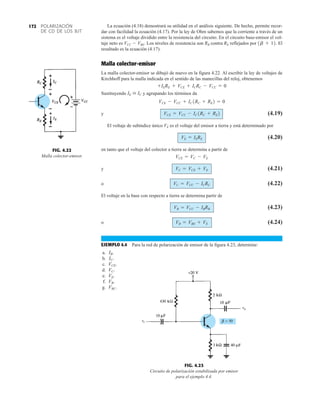

















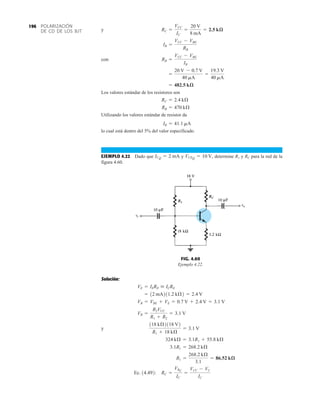

















































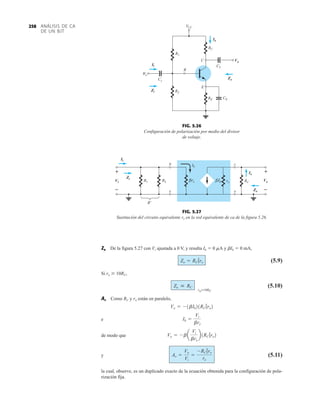





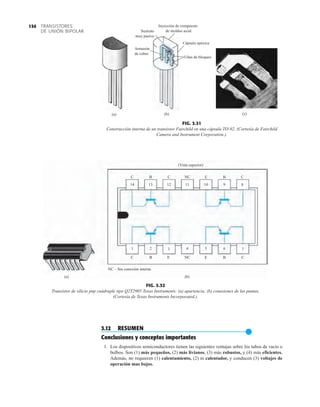
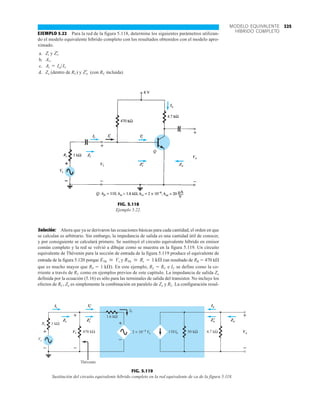
![ANÁLISIS DE CA
DE UN BJT
264 c.
d. se satisface. Por consiguiente,
comparado con 3.93 utilizando la ecuación (5.20): Av RCRE
Mathcad
Las extensas ecuaciones que resultan del análisis de la configuración de polarización en emisor
común demuestran el valor de ser experto en el uso del paquete de software Mathcad.
Las prioridades no permiten una descripción en detalle de cada paso del proceso, pero pode-
mos hacer algunos comentarios. En primer lugar, todos los parámetros de la red que aparecerán
en las ecuaciones deben definirse como se muestra en la figura 5.33. A continuación, se ingre-
san las ecuaciones para cada una de las cantidades deseadas como se muestra en la figura 5.33.
A continuación se ingresan las ecuaciones para cada una de las cantidades deseadas, teniendo
gran cuidado de incluir paréntesis en los lugares apropiados para asegurarse de que la ecuación
resultante sea la correcta. En realidad, aparecen más paréntesis de los necesarios, pero son el re-
sultado de un esfuerzo para que las ecuaciones se parezcan lo más posible a las que aparecen
en el texto. Una vez que se ha definido cada ecuación, su valor se determina con sólo ingresar
otra vez el nombre de la variable y hacer clic en el signo igual. Éste se muestra a la derecha de
3.89
Av =
Vo
Vi
-
bRC
Zb
= -
1120212.2 kÆ2
67.92 kÆ
ro Ú 10RC
Zo = RC = 2.2 kæ
VCC := 20.V VBE := 0.7.V Bf := 120
RB := 470.kΩ RC := 2.2.kΩ RE := 0.56.kΩ ro := 40.kΩ
IB :=
IE := (Bf + 1).IB
re := 26.
Zb := Bf.re +
Zi := RB.
Z := ro +
Zo :=
Av :=
(VCC - VBE)
RB + (Bf + 1).RE
(RC – Z)
(RC + Z)
mV
IE
(Bf + 1) +
RC
ro
(RC + RE)
ro
1 +
.RE
Zb
(RB + Zb)
[Bf.(ro + re)]
(Bf.re)
RE
1 +
Bf.RC
Z
1 + +
re
ro
RC
ro
RC
ro
1 +
.
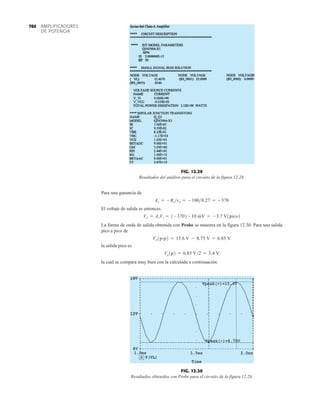
( (
(
( (
(
IB = 3.589 x 10-5
A
IE = 4.343 x 10-3
A
re = 5.987Ω
Zi = 5.643 x 104
Ω
Zo = 2.198 x 103
Ω
Av = –3.995
Ex. 5.6 re=5.99ohms
Ex. 5.6 Zi=59.34kilohms
Ex. 5.6 Zo=2.2kilohms
Ex. 5.6 Av=-3.89
FIG. 5.33
Parámetros y ecuaciones de red para el ejemplo 5.3.](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-283-320.jpg)






























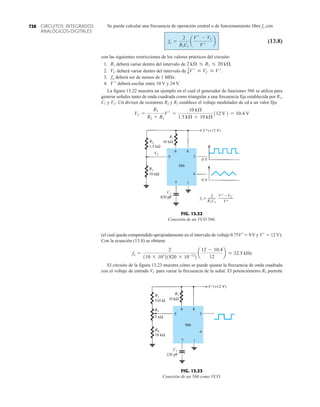
![FIG. 5.82
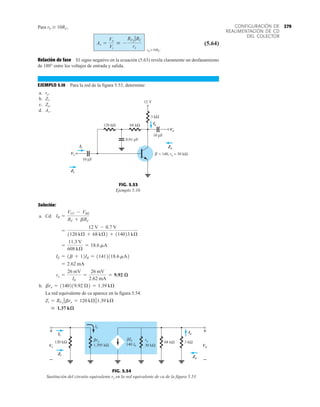
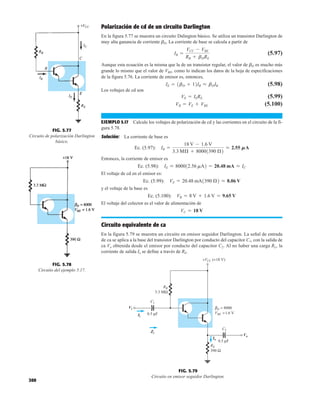
Determinación de Zo.
Impedancia de salida
La impedancia de salida se determinará regresando a la figura 5.81 y estableciendo Vi igual a
cero volts como se muestra en la figura 5.82. El resistor está “en cortocircuito” y el resultado es
la configuración de la figura 5.83. Observe en las figuras 5.82 y 5.83 que la corriente de salida
se redefinió para que concordara con la nomenclatura estándar y Zo correctamente definida.
303
CONEXIÓN
DARLINGTON
En el punto a la ley de la corriente de Kirchhoff dará
Al aplicar la ley de voltajes de Kirchhoff alrededor de toda la malla externa obtendremos
y
Sustituyendo
y
con
de modo que
Regresando
o Io =
Vo
RE
+
(b1 + 1)(b2 + 1)Vo
b1re1
+ (b1 + 1)b2re2
Io = Ie - (b2 + 1)Ib2
= Ie - (b2 + 1)a -
(b1 + 1)Vo
b1re1
+ (b1 + 1)b2re2
b
Ib2
= - c
b1 + 1
b1re1
+ (b1 + 1)b2re2
dVo
Ib2
= (b1 + 1)Ib1
= (b1 + 1)c -
Vo
b1re1
+ (b1 + 1)b2re2
d
Ib1
= -
Vo
b1re1
+ (b1 + 1)b2re2
= -Ib1
[b1re1
+ (b1 + 1)b2re2
]
Vo = -Ib1
b1re1
- (b1 + 1)Ib1
b2re2
Ib2
= (b1 + 1)Ib1
Vo = Ib1
b1re1
+ Ib2
b2re2
-Ib1
b1re1
- Ib2
b2re2
- Vo = 0
Io = Ie - (b2 + 1)Ib2
Io + (b2 + 1)Ib2
= Ie
RB RE Vo
Vi 0 V
Io
Ib1
Ib2
+
–
1re1
β 2re2
β
2Ib2
β
1Ib1
β
Zo
FIG. 5.83
Red de la figura 5.83 vuelta a dibujar.
RE Vo
Ib1
Ib2 Io
Ie
a
+
+
+
–
–
– 2re2
1re1 1Ib1 2Ib2
Zo](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-322-320.jpg)

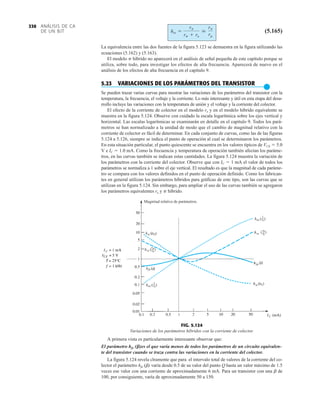
![y la terminal emisor del circuito Darlington está conectada a tierra cuando las condiciones son
de ca. Como se observa en la figura 5.85, se da la beta de cada transistor junto con el voltaje re-
sultante de la base al emisor.
El análisis de cd puede proseguir como sigue:
Utilizando los resultados precedentes se pueden determinar los valores y :
y
Impedancia de entrada
El equivalente de ca de la figura 5.85 aparece como la figura 5.86. Los resistores R1 y R2 están
en paralelo con la impedancia de entrada hacia el par Darlington, suponiendo que el segundo
transistor actúe como una carga RE sobre el primero, como se muestra en la figura 5.86.
Es decir, Zi¿ = b1re1
+ b1(b2re2
)
re1
=
26 mV
IE1
=
26 mV
0.095 mA
= 273.7 Æ
IE1
= IB2
=
IE2
b2
=
10.46 mA
110
= 0.095 mA
re2
=
26 mV
IE2
=
26 mV
10.46 mA
= 2.49 æ
re1
re2
IB =
IE
bD
=
10.46 mA
12,100
= 0.864 mA
IE =
VE
RE
=
7.11 V
680 Æ
= 10.46 mA
VE = VB - VBE = 8.61 V - 1.5 V = 7.11 V
VB =
R2
R2 + R1
VCC =
220 kÆ (27 V)
220 kÆ + 470 kÆ
= 8.61 V
FIG. 5.86
Definición de .
Zi¿ y Zi
Vi
Vo
Io
R1 R2
2re2
RC
Ii
Q1
Q2
Zi
Zi
'
2re2
Q1
Vi
Zi
Ii
Vo
Io
y (5.107)
Para la red de la figura 5.85:
y
42.97 kæ
= 149.86 kÆ || 60.24 kÆ
= 470 kÆ || 220 kÆ || 60.24 kÆ
Zi = R1 || R2 || Zi¿
60.24 kæ
= 110[547.6 Æ]
= 110[273.7 Æ + 273.9 Æ]
Zi¿ = 110[273.7 Æ + (110)(2.49 Æ)]
Zi¿ = b1[re1
+ b2re2
]
CONEXIÓN
DARLINGTON
305](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-324-320.jpg)















































![TRANSISTORES DE
EFECTO DE CAMPO
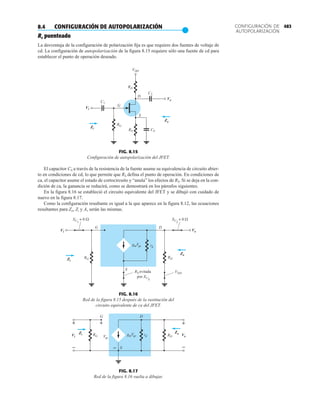
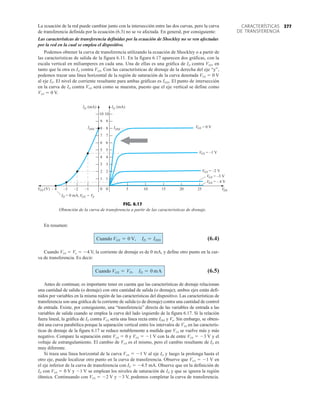
378 La curva de transferencia de ID contra VGS es la que se utilizará con frecuencia en el análisis del
capítulo 7 y no las características de la figura 6.17. En los párrafos siguientes presentaremos
un método rápido y eficiente de graficar ID contra VGS dados sólo los niveles de IDSS y la ecua-
ción de Shockley.
Aplicación de la ecuación de Shockley
La curva de transferencia de la figura 6.17 también se puede obtener de forma directa con la
ecuación de Shockley (6.3) dados simplemente los valores de IDSS y Vp. Los niveles de IDSS y Vp
definen los límites de la curva en ambos ejes y sólo se requiere localizar algunos puntos inter-
medios en la gráfica. La validez de la ecuación (6.3) como origen de la curva de transferencia
de la figura 6.17 se demuestra mejor examinando algunos niveles específicos de una variable
y determinando el nivel resultante de los demás como sigue:
Sustituyendo VGS 0 V da
y (6.6)
Sustituyendo VGS Vp tenemos
(6.7)
Para las características de drenaje de la figura 6.17, si sustituimos VGS 1 V
como se muestra en la figura 6.17. Observe el cuidado que se tuvo con los signos negativos para
VGS y Vp en los cálculos anteriores. La pérdida de un signo daría lugar a un resultado totalmente
erróneo.
Sería obvio que dados IDSS y Vp (como normalmente de dan en las hojas de especificaciones),
el nivel de ID se pudiera calcular para cualquier nivel de VGS. A la inversa, utilizando álgebra
básica podemos obtener [a partir de la ec. (6.3)] una ecuación para el nivel resultante de VGS
para un nivel dado de ID. La derivación es bastante directa y resulta
(6.8)
Comprobemos la ecuación (6.8) determinando el nivel de VGS que produzca una corriente de
drenaje de 4.5 mA para el dispositivo con las características de la figura 6.17. Encontramos
como se sustituyó en el cálculo anterior y se verificó en la figura 6.17.
= 1 V
= -4 V10.252
= -4 V11 - 10.56252 = -4 V11 - 0.752
VGS = -4 Va1 -
A
4.5 mA
8 mA
b
VGS = VP a1 -
A
ID
IDSS
b
= 4.5 mA
= 8 mA10.56252
= 8 mA a1 -
-1 V
-4 V
b
2
= 8 mA a1 -
1
4
b
2
= 8 mA10.7522
ID = IDSS a1 -
VGS
VP
b
2
ID = 0 AƒVGS =VP
= IDSS 11 - 122
= IDSS 102
ID = IDSS a1 -
VP
VP
b
2
ID = IDSS ƒ VGS =0 V
= IDSS a1 -
0
VP
b
2
= IDSS11 - 022
Ec. (6.3): ID = IDSS a1 -
VGS
VP
b
2](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-397-320.jpg)










![393
MOSFET TIPO
ENRIQUECIMIENTO
cargas semejantes se repelen) en el sustrato p a lo largo del borde de la capa de SiO3 para que
abandonen el área y lleguen a regiones más profundas del sustrato p, como se muestra en la
figura. El resultado es una región de empobrecimiento cerca de la capa aislante de SiO2 libre
de huecos. Sin embargo, los electrones en el sustrato tipo p (los portadores minoritarios del
material) serán atraídos a la compuerta positiva y se acumularán en la región cercana a la su-
perficie de la capa de SiO2. Ésta y sus propiedades aislantes impedirán que los portadores ne-
gativos sean absorbidos en la compuerta. Conforme VGS se incrementa, la concentración de
electrones cerca de la superficie de SiO3 se incrementa y con el tiempo la región tipo n indu-
cida puede soportar un flujo mensurable entra el drenaje y la fuente. El nivel de VGS que pro-
duce el incremento significativo de la corriente de drenaje se llama voltaje de umbral y está
dado por el símbolo VT. En las hojas de especificaciones se conoce como VGS(Th), aun cuando
VT es más difícil de manejar se utilizará en el análisis siguiente. Como el canal no existe con
VGS 0 V y está “mejorado” por la aplicación de un voltaje positivo de la compuerta a la
fuente, este tipo de MOSFET se llama MOSFET tipo enriquecimiento. Los MOSFET tipo
empobrecimiento –y enriquecimiento– tienen regiones tipo enriquecimiento, pero la etique-
ta se aplicó al segundo, puesto que es el único modo de operación.
Conforme VGS se incrementa más allá del nivel de umbral, la densidad de los electrones libres
en el canal inducido aumentará y el resultado es el nivel incrementado de la corriente de drenaje.
Sin embargo, si mantenemos VGS constante y aumentamos el nivel de VDS, la corriente de drenaje
con el tiempo alcanzará un nivel de saturación como ocurrió para el JFET y el MOSFET tipo
empobrecimiento. La nivelación de ID se debe a un proceso de estrangulamiento ilustrado por el
canal más angosto en el extremo de drenaje del canal inducido como se muestra en la figura 6.37.
Al aplicar la ley de voltajes de Kirchhoff a los voltajes en las terminales del MOSFET de la
figura 6.37, encontramos que
(6.13)
Si VGS se mantiene fijo a algún valor como 8 V y VDS se incrementa de 2 V a 5 V, el voltaje
VDG [de acuerdo con la ec. (6.31)] se reducirá de 6 V a 3 V y la compuerta se volverá cada
vez más negativa con respecto al drenaje. Esta reducción del voltaje de la compuerta al drenaje,
a su vez, reducirá las fuerzas de atracción para los portadores libres (electrones) en esta región del
canal inducido, provocando una reducción en el ancho efectivo del canal. A la larga, el canal se
reducirá hasta el punto de estrangulamiento y se establecerá una condición de saturación como
VDG = VDS - VGS
n
p
SS
S
D
+
I = 0 A
G
ID
+
+
+
+
+
+
+
+
+
+
+
+
Huecos repelidos por
la compuerta positiva.
Capa aislante
G
I = I
S D
e
e
e
e
e
e
e
n
Electrones atraídos a la compuerta
positiva (canal n inducido)
Región sin portadores
tipo p (huecos)
e
–
+
S
VG
–
+
S
VD
FIG. 6.36
Formación de un canal en un MOSFET tipo enriqueci-
miento de canal n.](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-412-320.jpg)

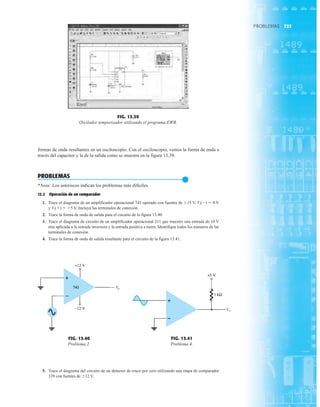
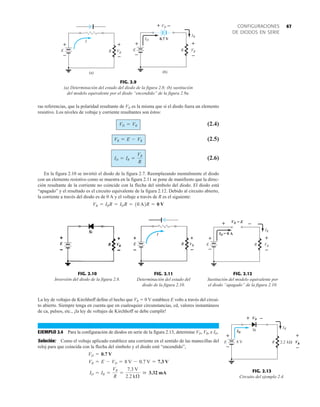
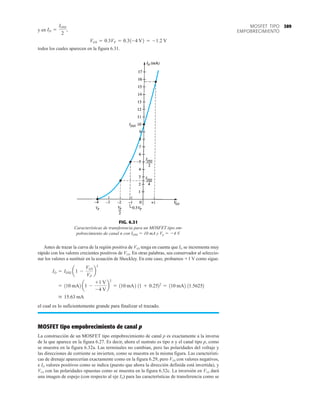
![395
MOSFET TIPO
ENRIQUECIMIENTO
VT
1 2 3 4 5 6
1
2
3
4
5
6
7
8
9
VGS
ID (mA)
VDS
0 7 8
10
2
3
4
5
6
8
9
0 5 10 15 20 25
VGS = +8 V
VGS = +7 V
VGS = +6 V
VGS = +5 V
VGS = +4 V
VGS = +3 V
ID (mA)
VGS = V = 2 V
T
10
7
1
FIG. 6.39
Trazo de las características de transferencia de un MOSFET tipo enriquecimiento de canal n a partir de las características de drenaje.
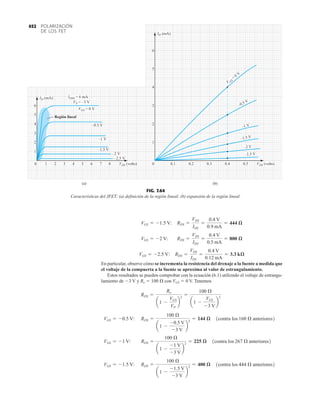
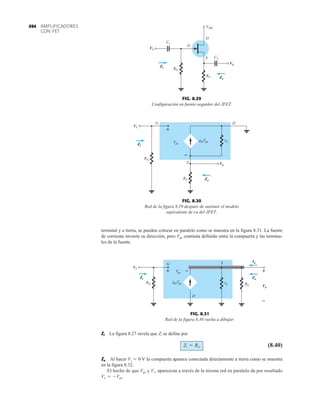
Para las características de la figura 6.37, el nivel de VT es de 2 V, como lo revela el hecho de
que la corriente de drenaje se redujo a 0 mA. En general, por consiguiente:
Para valores de VGS menores que el nivel de umbral, la corriente de drenaje de un MOSFET
tipo enriquecimiento es de 0 mA.
La figura 6.38 revela con claridad que a medida que el nivel de VGS se incrementa de VT
a 8 V, el nivel de saturación resultante de ID también se incrementa desde un nivel de 0 mA
hasta 10 mA. Además, es muy notable que la separación entre los niveles de VGS se incrementa
a medida que la magnitud de VGS lo hace, y el resultado son incrementos cada vez mayores de
la corriente de drenaje.
Para niveles de VGS VT, la corriente de drenaje está relacionada con el voltaje de la com-
puerta a la fuente aplicado por la siguiente relación no lineal:
(6.15)
De nueva cuenta, el término al cuadrado es el que produce la relación no lineal (curva) entre ID
y VGS. El término k es una constante que es una función de la construcción del dispositivo. El
valor de k se determina a partir de la siguiente ecuación [derivada de la ec. (6.15)], donde
ID(encenido) y VGS(encendido) son los valores de cada uno en un punto particular de las características
del dispositivo.
(6.16)
Sustituyendo ID(encendido) 10 mA cuando VGS(encendido) 8 V tomado de las características de la
figura 6.38 resulta
y una ecuación general para ID con las características de la figura 6.38 da como resultado
Sustituyendo VGS 4 V, encontramos que
comprobado por la figura 6.38. Con VGS VT, el término al cuadrado es 0, e ID 0 mA.
Para el análisis de los MOSFET tipo enriquecimiento que aparecerá en el capítulo 7, las carac-
terísticas de transferencia de nuevo serán las características que se emplearán en la solución gráfi-
ca. En la figura 6.39, las características de drenaje y transferencia se pusieron una al lado de otra
= 0.278 * 10-3
142 = 1.11 mA
ID = 0.278 * 10-3
14 V - 2 V22
= 0.278 * 10-3
1222
ID = 0.278 * 10-3
1VGS - 2 V22
= 0.278 : 10-3
A/V2
k =
10 mA
18 V - 2 V22 =
10 mA
16 V22 =
10 mA
36 V2
k =
ID1encendido2
1VGS1encendido2 - VT22
ID = k1VGS - VT22](https://image.slidesharecdn.com/semana10-230526154235-279e2c6b/85/semana-N-10-414-320.jpg)