Este documento describe el análisis semántico en los procesadores de lenguaje. Explica que el análisis semántico detecta errores que no fueron detectados sintácticamente y obtiene un árbol de sintaxis abstracta decorado con información. También utiliza esquemas de traducción dirigidos por la sintaxis que asocian acciones a las reglas gramaticales para realizar comprobaciones y construir el árbol.

1. 4o Ingenier´ Inform´tica
ıa a
II26 Procesadores de lenguaje
An´lisis sem´ntico
a a
Esquema del tema
1. Introducci´n
o
2. Esquemas de traducci´n dirigidos por la sintaxis
o
3. El ´rbol de sintaxis abstracta
a
4. Comprobaciones sem´nticas
a
5. Interpretaci´n
o
6. Introducci´n a metacomp
o
7. Algunas aplicaciones
8. Resumen del tema
1. Introducci´n
o
Hay determinadas caracter´ ısticas de los lenguajes de programaci´n que no pueden ser mode-
o
ladas mediante gram´ticas incontextuales y que es necesario comprobar en una fase posterior al
a
an´lisis sint´ctico. Por otro lado, las fases posteriores de la compilaci´n o interpretaci´n necesitan
a a o o
una representaci´n de la entrada que les permita llevar a cabo sus funciones de manera adecuada.
o
Estas dos vertientes —detecci´n de errores y representaci´n de la informaci´n— est´n muy
o o o a
relacionadas y se solapan en la pr´ctica. Supongamos, por ejemplo, que nuestro lenguaje permite
a
asignaciones seg´n la regla
u
Asignaci´n → id:= Expresi´n ;
o o
Es habitual que se impongan ciertas restricciones. En nuestro caso, estas podr´ ser:
ıan
El identificador de la parte izquierda debe estar declarado previamente.
El tipo de la expresi´n debe ser compatible con el del identificador.
o
El analizador sem´ntico deber´ comprobar que estas dos restricciones se cumplen antes de decla-
a a
rar que la sentencia de asignaci´n est´ bien formada. Pero sucede que la informaci´n necesaria
o a o
para comprobarlas es util tambi´n para generar c´digo. Esto quiere decir que si tuvi´ramos una
´ e o e
separaci´n estricta entre las fases del compilador, para generar c´digo deber´
o o ıamos volver a mirar
el identificador para saber a qu´ objeto (variable, funci´n, constante, etc.) corresponde y qu´ tipo
e o e
tiene y tambi´n deber´
e ıamos volver a comprobar los tipos de la expresi´n para generar el c´digo
o o
adecuado.
Por otro lado, aunque en teor´ el arbol de an´lisis ser´ suficiente para fases posteriores de la
ıa ´ a ıa
compilaci´n o interpretaci´n, es una representaci´n que contiene mucha informaci´n redundante.
o o o o
As´ el ´rbol correspondiente a a:= b+c; bien podr´ tener el aspecto del ´rbol de la izquierda,
ı, a ıa a
cuando el de la derecha contiene esencialmente la misma informaci´n y resulta m´s c´modo para
o a o

2. 2 II26 Procesadores de lenguaje
trabajar:
Asignaci´n
o
ida := Expresi´n
o ;
asignaci´n
o
Expresi´n
o + T´rmino
e
variablea suma
T´rmino
e Factor
variableb constantec
Factor idc
idb
El segundo ´rbol se conoce como ´rbol de sintaxis abstracta (o AST, de las iniciales en ingl´s).
a a e
Como hemos comentado, durante el an´lisis sem´ntico se recoge una serie de informaciones que
a a
resultan de utilidad para fases posteriores. Estas informaciones se pueden almacenar en el ´rbol,
a
“decor´ndolo”:
a
asignaci´n
o
variable suma
nombre: a tipo: entero
tipo: entero
variable constante
nombre: b nombre: c
tipo: entero tipo: entero
valor: 5
As´ el objetivo de la fase de an´lisis sem´ntico ser´ doble: por un lado detectaremos errores que
ı a a a
no se han detectado en fases previas y por otro lado obtendremos el AST decorado de la entrada.
Para ello utilizaremos esquemas de traducci´n dirigidos por la sintaxis, que permitir´n asociar
o a
acciones a las reglas de la gram´tica. Estas acciones realizar´n comprobaciones y construir´n el
a a a
AST que despu´s se recorrer´ para terminar las comprobaciones y ser´ la base para la interpreta-
e a a
ci´n o la generaci´n de c´digo.
o o o
2. Esquemas de traducci´n dirigidos por la sintaxis
o
Nuestro objetivo es especificar una serie de acciones que se realizar´n durante el an´lisis de
a a
la entrada y tener un mecanismo que nos permita obtener la informaci´n necesaria para realizar
o
estas acciones. Para esto a˜adimos a las gram´ticas dos elementos nuevos:
n a
Acciones intercaladas en las reglas.
Atributos asociados a los no terminales de la gram´tica.
a
2.1. Acciones intercaladas en las reglas
Supongamos que tenemos el no terminal A que deriva dos partes diferenciadas y queremos
que se escriba el mensaje “Cambio de parte” tras analizarse la primera. Podemos describir esto

3. An´lisis sem´ntico
a a 3
de forma sencilla si aumentamos nuestra gram´tica incluyendo la acci´n en la parte derecha de la
a o
regla de A :
A → Parte1 {escribe(“Cambio de parte”);} Parte2
Podemos entender esta regla extendida como la receta: “analiza la primera parte, una vez
encontrada, escribe el mensaje y despu´s analiza la segunda parte”.
e
2.2. Atributos asociados a los no terminales
Si nuestras acciones se limitaran a escribir mensajes que indicaran la fase del an´lisis en la que
a
nos encontramos, no necesitar´ ıamos mucho m´s. En general, querremos que las acciones respondan
a
al contenido de los programas que escribimos. Para ello, vamos a a˜adir a los no terminales una serie
n
de atributos. Estos no son m´s que una generalizaci´n de los atributos que tienen los terminales.
a o
Vamos a ver un ejemplo.
Supongamos que en un lenguaje de programaci´n se exige que en las subrutinas aparezca un
o
identificador en la cabecera que debe coincidir con el que aparece al final. Tenemos el siguiente
fragmento de la gram´tica del lenguaje:
a
Subrutina → Cabecera Cuerpo Fin
Cabecera → subrutina id( Par´metros );
a
Fin → fin id
En la regla correspondiente a Fin querremos comprobar que el identificador es el mismo que
en la cabecera. Vamos a definir un atributo del no terminal Fin que ser´ el que nos diga el nombre
a
de la funci´n:
o
Fin → fin id {si id.lexema = Fin .nombre entonces error fin si}
El atributo nombre es lo que se conoce como un atributo heredado: su valor se calcular´ en las
a
reglas en las que Fin aparezca en la parte derecha y se podr´ utilizar en las reglas en las que Fin
a
aparezca en la izquierda; ser´ informaci´n que “heredar´” de su entorno. F´
a o a ıjate en c´mo hemos
o
empleado un atributo de id para hacer comprobaciones. El analizador sem´ntico es el que emplea
a
la informaci´n contenida en los atributos de los componentes l´xicos. Recuerda que el sint´ctico
o e a
s´lo ve las etiquetas de las categor´ En cuanto a error, suponemos que representa las acciones
o ıas.
necesarias para tratar el error.
Ahora tenemos que completar las acciones de modo que Fin tenga alg´n valor para el nombre.
u
Podemos a˜adir una acci´n a la regla de Subrutina para calcular el valor de Fin .nombre:
n o
Subrutina → Cabecera Cuerpo { Fin .nombre:= Cabecera .nombre} Fin
Lo que hacemos es copiar el atributo nombre que nos “devolver´” Cabecera . No debes confundir
a
el atributo nombre de Fin con el de Cabecera , son completamente independientes. De hecho, el
atributo nombre de Cabecera es un atributo sintetizado: su valor se calcular´ en las reglas en las
a
que Cabecera aparezca en la parte izquierda y se utilizar´ en las reglas donde Cabecera aparezca
a
en la parte derecha; es informaci´n que Cabecera “sintetiza” para su entorno. Debemos calcular
o
el valor de nombre en la regla de Cabecera :
Cabecera → subrutina id( Par´metros ); { Cabecera .nombre:= id.lexema}
a
2.3. Otros elementos de las acciones
Como habr´s comprobado, no hemos definido ning´n lenguaje formal para escribir las acciones.
a u
Asumiremos que se emplean construcciones corrientes de los algoritmos tales como condicionales
c Universitat Jaume I 2006-2007

4. 4 II26 Procesadores de lenguaje
o bucles. Tambi´n haremos referencia en ellos a subrutinas y a variables. Las variables las inter-
e
pretaremos como variables locales a la regla que estamos analizando o como variables globales si
lo indicamos expl´
ıcitamente. As´ en:
ı,
Valor → opsum {si opsum.lexema=“+” entonces signo:= 1 si no signo:= -1 fin si}
Valor 1 { Valor .v:= signo* Valor 1 .v}
no hay ninguna “interferencia” entre las distintas variables signo que se puedan utilizar en un mo-
mento dado. F´ ıjate tambi´n en c´mo hemos distinguido mediante un sub´
e o ındice las dos apariciones
del no terminal Valor .
Un recurso muy util son los atributos que contienen listas. Por ejemplo, para una declaraci´n
´ o
de variables del tipo:
DeclVariables → ListaIds : Tipo
ListaIds → id, ListaIds |id
podemos hacer lo siguiente:
DeclVariables → ListaIds : Tipo
{para v en ListaIds .l hacer: declara_var(v, Tipo .t) fin para}
ListaIds → id, ListaIds 1 { ListaIds .l:= concat( [id.lexema], ListaIds 1 .l)}
ListaIds → id { ListaIds .l:= [id.lexema]}
2.4. Recopilaci´n
o
Con lo que hemos visto, podemos decir que un esquema de traducci´n consta de:
o
Una gram´tica incontextual que le sirve de soporte.
a
Un conjunto de atributos asociados a los s´
ımbolos terminales y no terminales.
Un conjunto de acciones asociadas a las partes derechas de las reglas.
Dividimos los atributos en dos grupos:
Atributos heredados.
Atributos sintetizados.
Sea A → X1 . . . Xn una producci´n de nuestra gram´tica. Exigiremos que:
o a
Las acciones de la regla calculen todos los atributos sintetizados de A .
Las acciones situadas a la izquierda de Xi calculen todos los atributos heredados de Xi .
Ninguna acci´n haga referencia a los atributos sintetizados de los no terminales situados a
o
su derecha en la producci´n.
o
Las dos ultimas reglas nos permitir´n integrar las acciones sem´nticas en los analizadores descen-
´ a a
dentes recursivos. Cuando se emplean, se dice que el esquema de traducci´n est´ basado en una
o a
gram´tica L-atribuida. La L indica que el an´lisis y evaluaci´n de los atributos se pueden hacer de
a a o
izquierda a derecha.

5. An´lisis sem´ntico
a a 5
Ejercicio 1
Las siguientes reglas representan parte de las sentencias estructuradas de un lenguaje de pro-
gramaci´n:
o
Programa → Sentencias
Sentencias → Sentencia Sentencias | Sentencia
Sentencia → mientras Expresi´n hacer Sentencias finmientras
o
Sentencia → si Expresi´n entonces Sentencias sino Sentencias finsi
o
Sentencia → interrumpir
Sentencia → otros
A˜ade las reglas necesarias para comprobar que la instrucci´n interrumpir aparece unicamente
n o ´
dentro de un bucle.
Ejercicio 2
Sea G la siguiente gram´tica:
a
A → B C |a
B → A a B b| C a
C → a C C |aba C |a
A˜ade a G las reglas sem´nticas necesarias para que el atributo ia de A contenga el n´mero
n a u
de aes al inicio de la cadena generada. Por ejemplo, dadas las cadenas aaaaba, abaaaa y aaa, los
valores de ia ser´ 4, 1 y 3, respectivamente.
ıan
Puedes utilizar los atributos adicionales que consideres necesarios, pero ninguna variable global.
Adem´s, los atributos que a˜adas deben ser de tipo entero o l´gico.
a n o
2.5. Algunas cuestiones formales
Una pregunta razonable es si puede el s´ ımbolo inicial tener atributos heredados y, si esto es
as´ de d´nde proceden. La respuesta var´ seg´n los textos. Los que se oponen, defienden que el
ı, o ıa u
significado del programa debe depender unicamente de ´l. Los que est´n a favor de los atributos
´ e a
heredados, sostienen que permiten formalizar la entrada de informaci´n acerca de, por ejemplo, el
o
entorno donde se ejecutar´ el programa o las opciones de compilaci´n.
a o
Una situaci´n similar se da con los s´
o ımbolos terminales: hay autores que piensan que no deber´ıan
tener atributos en absoluto; otros defienden que s´lo deben tener atributos sintetizados; y los hay
o
que opinan que pueden tener tanto atributos heredados como sintetizados.
Otro aspecto sobre el que hay diferencias de interpretaci´n es el de los efectos laterales de las
o
reglas. En algunos textos, las reglas de evaluaci´n de los atributos no pueden tener efectos laterales.
o
Otros autores defienden que esta distinci´n no es m´s que un problema de implementaci´n ya que
o a o
es posible a˜adir un nuevo atributo que represente el entorno e ir actualiz´ndolo adecuadamente.
n a
Esto unicamente supone una incomodidad, pero no un problema formal. Esta es la posici´n que
´ o
seguiremos nosotros, permitiendo que haya efectos laterales en el c´lculo de atributos.
a
Quiz´ los ejemplos m´s claros de existencia de efectos laterales sean el manejo de la tabla de
a a
s´
ımbolos y el control de errores. Cuando se encuentra una declaraci´n en un programa es necesario
o
actualizar la tabla de s´ ımbolos de modo que sea posible reconocer ocurrencias posteriores del
identificador. Podemos suponer que existe una tabla de s´ ımbolos global o tener un atributo que
lleve copias de la tabla de un sitio a otro.
Por otro lado, en caso de que se encuentre un error, es necesario tomar medidas como detener
la generaci´n de c´digo. Una manera sencilla de marcar esta circunstancia es tener una variable
o o
c Universitat Jaume I 2006-2007

6. 6 II26 Procesadores de lenguaje
global de tipo l´gico que indique si se ha encontrado alg´n error. Nuevamente, ser´ posible, pero
o u ıa
no necesario, tener un atributo que transporte esa informaci´n.
o
2.6. Eliminaci´n de recursividad por la izquierda y atributos
o
En el tema de an´lisis sint´ctico vimos c´mo se pueden modificar las producciones con recursivi-
a a o
dad por la izquierda para lograr que la gram´tica sea LL(1). El problema con las transformaciones
a
es que dejan una gram´tica que tiene muy poca relaci´n con la original, lo que hace que escribir los
a o
atributos y las reglas correspondientes sea dif´ sobre la gram´tica transformada. Sin embargo,
ıcil a
se pueden escribir los atributos sobre la gram´tica original y despu´s convertirlos de una manera
a e
bastante mec´nica.
a
Como las GPDRs no suelen necesitar recursividad por la izquierda, es f´cil que no tengas que
a
utilizar esta transformaci´n. Pese a todo, vamos a ver c´mo se hace la transformaci´n sobre un
o o o
ejemplo. Partimos del siguiente esquema de traducci´n:o
E → E 1 + T { E .v:= E 1 .v+ T .v}
E → T { E .v:= T .v}
T → num { T .v:= num.v}
Comenzamos por transformar la gram´tica:
a
E → T E’
E’ → + T E’
E’ → λ
T → num
Como vemos, el problema es que cuando vemos el sumando derecho en E’ , no tenemos acceso
al izquierdo. La idea ser´ crear un atributo heredado que nos diga el valor del sumando izquierdo.
a
En la primera regla lo podemos calcular directamente. En la segunda regla, realizamos la suma y
la transmitimos:
E → T { E’ .h:= T .v} E’
E’ → + T { E’ 1 .h:= E’ .h+ T .v} E’ 1
Con esto, el atributo h contendr´ siempre la suma, que es el valor que tenemos que devolver
a
finalmente. Por eso hay que “transmitir” el nuevo valor al atributo v:
E → T { E’ .h:= T .v } E’ { E .v:= E’ .v}
E’ → + T { E’ 1 .h:= E’ .h+ T .v} E’ 1 { E’ .v:= E’ 1 .v}
¿Qu´ hacemos cuando E’ se reescribe como la cadena vac´ En este caso, basta con devolver
e ıa?
como sintetizado el valor que se hereda. El esquema de traducci´n completo queda:
o
E → T { E’ .h:= T .v} E’ { E .v:= E’ .v}
E’ → + T { E’ 1 .h:= E’ .h+ T .v} E’ 1 { E’ .v:= E’ 1 .v}
E’ → λ { E’ .v:= E’ .h}
T → num { T .v:= num.v}
Ejercicio 3
Escribe el ´rbol de an´lisis de 3+4 con el esquema original y el transformado. Dec´ralos.
a a o

7. An´lisis sem´ntico
a a 7
Ejercicio 4
Transforma el siguiente esquema de traducci´n para eliminar la recursividad por la izquierda:
o
E → E 1 + T { E .v:= E 1 .v+ T .v}
E → T { E .v:= T .v}
T → T 1 * F { T .v:= T 1 .v* F .v}
T → F { T .v:= F .v}
F → ( E ) { F .v:= E .v}
F → num { F .v:= num.v}
El siguiente ejercicio presenta la transformaci´n de una manera m´s general.
o a
Ejercicio* 5
Si tenemos las siguientes reglas en un esquema de traducci´n
o
A → A 1 Y { A .a:= g( A 1 .a, Y .y)}
A → X { A .a:= f( X .x)}
podemos transformarlas en
A → X { A’ .h:= f( X .x)} A’ { A .a:= A’ .s}
A’ → Y { A’ 1 .h:= g( A’ .h, Y .y)} A’ 1 { A’ .s:= A’ 1 .s}
A’ → λ { A’ .s:= A’ .h}
Comprueba que la transformaci´n es correcta analizando X Y 1 Y 2 mediante las dos versiones y
o
comparando el valor de a.
2.7. Implementaci´n de los esquemas de traducci´n
o o
La interpretaci´n de las acciones como sentencias que se ejecutan al pasar el an´lisis por ellas
o a
permite implementar los esquemas de traducci´n de manera sencilla. Para ello se modifica la
o
implementaci´n del analizador recursivo descendente correspondiente a la gram´tica original de la
o a
siguiente manera:
Los atributos heredados del no terminal A se interpretan como par´metros de entrada de
a
la funci´n Analiza_A.
o
Los atributos sintetizados del no terminal A se interpretan como par´metros de salida de
a
la funci´n Analiza_A.
o
Las acciones sem´nticas, una vez traducidas al lenguaje de programaci´n correspondiente, se
a o
insertan en la posici´n correspondiente seg´n su orden en la parte derecha donde aparecen.
o u
En la pr´ctica, es frecuente que, si el lenguaje de programaci´n (como C) no permite devolver
a o
m´s de un valor, los atributos sintetizados del no terminal se pasen por referencia.
a
En Python existe una soluci´n bastante c´moda. Comenzamos por definir una clase vac´
o o ıa:
class Atributos:
pass
Antes de llamar a una funci´n o m´todo de an´lisis, creamos un objeto de esta clase y le
o e a
a˜adimos los atributos heredados del no terminal. La correspondiente funci´n de an´lisis crear´
n o a a
los atributos sintetizados. Este es el unico par´metro que se pasa. As´ la traducci´n de la regla:
´ a ı, o
c Universitat Jaume I 2006-2007

8. 8 II26 Procesadores de lenguaje
E → T { R .h:= T .v} R { E .v:= R .v}
es la siguiente:
def analiza_E(E):
T= Atributos() # Atributos de T
R= Atributos() # Atributos de R
analiza_T(T)
R.h= T.v # Creamos un atributo heredado de R
analiza_R(R)
E.v= R.v # Creamos un atributo sintetizado de E
L´gicamente, tendr´
o ıamos que haber a˜adido el c´digo de control de errores.
n o
2.8. Atributos en GPDR
La interpretaci´n que hemos hecho de los esquemas de traducci´n se traslada de forma natural
o o
a las GPDR. Por ejemplo, la traducci´n de:
o
E → T 1 { E .v:= T 1 .v}(+ T 2 { E .v:= E .v+ T 2 .v})∗
es simplemente:
def analiza_E(E):
T1= Atributos() # Atributos de T1
T2= Atributos() # Atributos de T2
analiza_T(T1)
E.v= T1.v
while token.cat=="suma":
token= alex.siguiente()
analiza_T(T2)
E.v= E.v+T2.v
Como antes, habr´ que a˜adir el correspondiente c´digo para controlar errores.
ıa n o
3. El ´rbol de sintaxis abstracta
a
Como hemos comentado en la introducci´n, una de las posibles representaciones sem´nticas de
o a
la entrada es el ´rbol de sintaxis abstracta o AST.
a
Aunque es similar a los ´rboles de an´lisis sint´ctico, tiene algunas diferencias importantes:
a a a
No aparecen todos los componentes l´xicos del programa. Por ejemplo:
e
• No es necesario incluir los par´ntesis de las expresiones.
e
• No se necesitan los separadores o terminadores de las sentencias.
• ...
Pueden aparecer otros componentes no estrictamente sint´cticos, como acciones de coerci´n
a o
de tipos.

9. An´lisis sem´ntico
a a 9
3.1. Construcci´n
o
Para construir los ´rboles, debemos comenzar por definir qu´ elementos emplearemos para cada
a e
estructura:
Estructura Representaci´n
o Estructura Representaci´n
o
si sentencias
if E then LS end begin S 1 . . . S n end
E LS S 1 ... Sn
mientras asignaci´n
o
while C do LS end id:= E ;
C LS id E
repetir suma
repeat LS until C ; E 1+ E 2
LS C E1 E2
... ... ... ...
F´
ıjate que el ´rbol resultante puede representar programas en diversos lenguajes de programa-
a
ci´n del estilo C, Pascal, etc.
o
Ahora debemos utilizar los atributos para construir el ´rbol. Utilizando el atributo arb para
a
devolver el ´rbol que construye cada no terminal, podemos hacer algo parecido a:
a
Sentencia → if Expresi´n then Sentencias end
o
{ Sentencia .arb:= NodoSi( Expresi´n .arb, Sentencias .arb)}
o
Sentencia → while Expresi´n do Sentencias end
o
{ Sentencia .arb:= NodoMientras( Expresi´n .arb, Sentencias .arb)}
o
Sentencia → repeat Sentencias until Expresi´n ;
o
{ Sentencia .arb:= NodoRepetir( Sentencias .arb, Expresi´n .arb)}
o
Sentencia → id:= Expresi´n ;
o
{ Sentencia .arb:= NodoAsignaci´n(id.lexema, Expresi´n .arb)}
o o
Para la implementaci´n hay dos opciones principales:
o
Utilizar funciones (NodoSi, NodoMientras, . . . ) que devuelvan una estructura de datos ade-
cuada.
Utilizar objetos (NodoSi, NodoMientras, . . . ) para cada uno de los nodos.
Probablemente, la segunda opci´n sea la m´s c´moda para el trabajo posterior con el ´rbol.
o a o a
En cuanto a la lista de sentencias, podemos utilizar nodos que tengan un grado variable, para
eso almacenamos una lista con los hijos:
Sentencias → {l:=λ} ( Sentencia {l:=l+ Sentencia .arb})∗
{ Sentencias .arb:= NodoSentencias(l)}
El tratamiento de las expresiones es sencillo. Por ejemplo, para la suma podemos hacer:
Expresi´n
o → T´rmino 1 {arb:= T´rmino 1 .arb}
e e
( + T´rmino 2 {arb:=NodoSuma(arb, T´rmino 2 .arb)})∗
e e
{ Expresi´n .arb:= arb}
o
c Universitat Jaume I 2006-2007

10. 10 II26 Procesadores de lenguaje
Las restas, productos, etc, se tratar´ de forma similar. Puedes comprobar que de esta manera
ıan
el AST resultante respeta la asociatividad por la izquierda.
Ejercicio* 6
En el caso de la asociatividad por la derecha tenemos dos opciones: crear una lista de operandos
y recorrerla en orden inverso para construir el ´rbol o utilizar recursividad por la derecha, que
a
no da problemas para el an´lisis LL(1). Utiliza ambas posibilidades para escribir sendos esque-
a
mas de traducci´n que construyan los AST para expresiones formadas por sumas y potencias de
o
identificadores siguiendo las reglas habituales de prioridad y asociatividad.
3.2. Evaluaci´n de atributos sobre el AST
o
Un aspecto interesante del AST es que se puede utilizar para evaluar los atributos sobre ´l, ene
lugar de sobre la gram´tica inicial. Si reflexionas sobre ello, es l´gico. Todo el proceso de evaluaci´n
a o o
de los atributos se puede ver como el etiquetado de un ´rbol (el ´rbol de an´lisis), pero no hay
a a a
nada que impida que el ´rbol sobre el que se realiza la evaluaci´n sea el AST.
a o
Un ejemplo ser´ el c´lculo de tipos. Si tenemos la expresi´n (2+3.5)*4, podemos calcular los
ıa a o
tipos sobre el ´rbol de an´lisis:
a a
Expresi´n
o
t: real
T´rmino
e
t: real
Factor * Factor
t: real t: entero
( Expresi´n
o ) num
t: real v: 4
t: entero
T´rmino
e + T´rmino
e
t: entero t: real
Factor Factor
t: entero t: real
num num
v: 2 v: 3.5
t: entero t: real

11. An´lisis sem´ntico
a a 11
o ıamos utilizar una gram´tica similar a la siguiente1 :
Para realizar esta evaluaci´n, podr´ a
Expresi´n
o → T´rmino 1 {t:= T´rmino 1 .t}(+ T´rmino 2 {t:= m´sgeneral(t, T´rmino 2 .t)})∗
e e e a e
{ Expresi´n .t:= t}
o
...
T´rmino
e → Factor 1 {t:= Factor 1 .t}(* Factor 2 {t:= m´sgeneral(t, Factor 2 .t)})∗
a
{ T´rmino .t:= t}
e
...
Factor → num { Factor .t:= num.t}
Factor → ( Expresi´n ) { Factor .t:= Expresi´n .t}
o o
...
Tambi´n podemos realizar el c´lculo sobre el AST:
e a
producto
t: real
suma num
t: real v: 4
t: entero
num num
v: 2 v: 3.5
t: entero t: real
Esto se har´ junto con el resto de comprobaciones sem´nticas.
ıa a
La elecci´n acerca de si evaluar atributos en el AST o durante el an´lisis descendente es b´si-
o a a
camente una cuesti´n de simplicidad. Generalmente, podemos decir que los atributos sintetizados
o
tienen una dificultad similar en ambos casos. Sin embargo, cuando la gram´tica ha sufrido trans-
a
formaciones o hay muchos atributos heredados, suele ser m´s f´cil evaluarlos sobre el AST.
a a
Otro aspecto interesante a la hora de decidir qu´ atributos evaluar sobre el ´rbol de an´lisis y
e a a
cu´les sobre el AST est´ en los propios nodos del ´rbol. Supongamos que queremos tener nodos
a a a
diferentes para la suma entera y la suma real. En este caso, tendremos que comprobar los tipos
directamente sobre el ´rbol de an´lisis (o crear un AST y despu´s modificarlo, pero esto puede ser
a a e
forzarlo demasiado).
4. Comprobaciones sem´nticas
a
Los atributos nos permitir´n llevar a cabo las comprobaciones sem´nticas que necesite el len-
a a
guaje. En algunos casos, utilizaremos los atributos directamente (posiblemente evaluados sobre el
AST), por ejemplo en la comprobaci´n que hac´
o ıamos de que el identificador al final de la funci´n
o
era el mismo que al principio.
En otros casos, los atributos se utilizan indirectamente mediante estructuras globales, por
ejemplo la tabla de s´
ımbolos. Un ejemplo ser´ la comprobaci´n de que un identificador no se ha
ıa o
declarado dos veces. Si hemos utilizado un nodo similar a:
1 Utilizamos la funci´n m´sgeneral que devuelve el tipo m´s general de los que se le pasan como par´metros (el
o a a a
tipo real se considera m´s general que el entero).
a
c Universitat Jaume I 2006-2007

12. 12 II26 Procesadores de lenguaje
declaraci´n
o
Tipo Listaids
el m´todo de comprobaci´n ser´
e o ıa:
Objeto NodoDeclaraci´n: o
...
M´todo compsem´nticas()
e a
...
para i ∈ listaids hacer
si TablaS´ımbolos.existe(i) entonces
error
si no
TablaS´ ımbolos.inserta(i, tipo)
fin si
fin para
...
fin compsem´nticas
a
...
fin NodoDeclaraci´no
Utilizando directamente el esquema de traducci´n habr´ que duplicar parte del c´digo:
o ıa o
Declaraci´n
o → Tipo { Listaids .t:= Tipo .t } Listaids
Listaids → id, { Listaids 1 .t:= Listaids .t} Listaids 1
{si TablaS´
ımbolos.existe(id.lexema)
entonces error
si no TablaS´
ımbolos.inserta(id.lexema, Listaids .t)}
Listaids → id
{si TablaS´
ımbolos.existe(id.lexema)
entonces error
si no TablaS´
ımbolos.inserta(id.lexema, Listaids .t)}
4.1. La tabla de s´
ımbolos
Durante la construcci´n del AST, las comprobaciones sem´nticas y, probablemente, durante la
o a
interpretaci´n y la generaci´n de c´digo necesitaremos obtener informaci´n asociada a los distintos
o o o o
identificadores presentes en el programa. La estructura de datos que permite almacenar y recuperar
esta informaci´n es la tabla de s´
o ımbolos.
En principio, la tabla debe ofrecer operaciones para:
Insertar informaci´n relativa a un identificador.
o
Recuperar la informaci´n a partir del identificador.
o
La estructura que puede realizar estas operaciones de manera eficiente es la tabla hash (que
en Python est´ disponible mediante los diccionarios). La implementaci´n habitual es una tabla
a o
que asocia cada identificador a informaci´n tal como su naturaleza (constante, variable, nombre de
o
funci´n, etc.), su tipo (entero, real, booleano, etc.), su valor (en el caso de constantes), su direcci´n
o o
(en el caso de variables y funciones), etc.
Es importante tener unicamente una tabla; si tenemos varias, por ejemplo, una para constantes
´
y otra para variables, el acceso se hace m´s dif´ ya que para comprobar las propiedades de un
a ıcil
identificador hay que hacer varias consultas en lugar de una.

13. An´lisis sem´ntico
a a 13
Una cuesti´n importante es c´mo se relacionan la tabla y el AST. Tenemos distintas posibili-
o o
dades, que explicaremos sobre el siguiente ´rbol, correspondiente a la sentencia a= a+c:
a
asignaci´n
o
variable suma
nombre: a tipo: entero
variable variable
nombre: a nombre: c
La primera posibilidad es dejar el ´rbol tal cual y cada vez que necesitemos alguna informaci´n,
a o
por ejemplo el valor de a, consultar la tabla. Esta opci´n ser´ la m´s adecuada para situaciones
o ıa a
en las que se vaya a recorrer el ´rbol pocas veces, por ejemplo en una calculadora donde se eval´e
a u
cada expresi´n una sola vez.
o
Otra posibilidad es ir decorando cada una de las hojas con toda la informaci´n que se vaya
o
recopilando. Por ejemplo, si durante el an´lisis averiguamos el tipo y direcci´n de las variables,
a o
pasar´ıamos a almacenar la nueva informaci´n: o
Tabla de s´
ımbolos
asignaci´n
o a: {tipo:entero, dir:1000}
...
variable suma c: {tipo:entero, dir:1008}
nombre: a tipo: entero
tipo: entero ...
dir: 1000
variable variable
nombre: a nombre: c
tipo: entero tipo: entero
dir: 1000 dir: 1008
Esto tiene costes muy elevados en tiempo —tendremos que actualizar repetidamente un n´mero
u
de nodos que puede ser elevado— y espacio —hay mucha informaci´n que se almacena repetida—.
o
Podemos reducir estos costes guardando en cada nodo un puntero a la entrada correspondiente en
la tabla:
Tabla de s´
ımbolos
a: {tipo:entero, dir:1000}
asignaci´n
o ...
c: {tipo:entero, dir:1008}
variable suma
...
tipo: entero
variable variable
Finalmente, la opci´n m´s adecuada cuando tenemos lenguajes que presenten ´mbitos anidados
o a a
(veremos en otro tema c´mo representar los ´mbitos en la tabla) es guardar la informaci´n sobre
o a o
c Universitat Jaume I 2006-2007

14. 14 II26 Procesadores de lenguaje
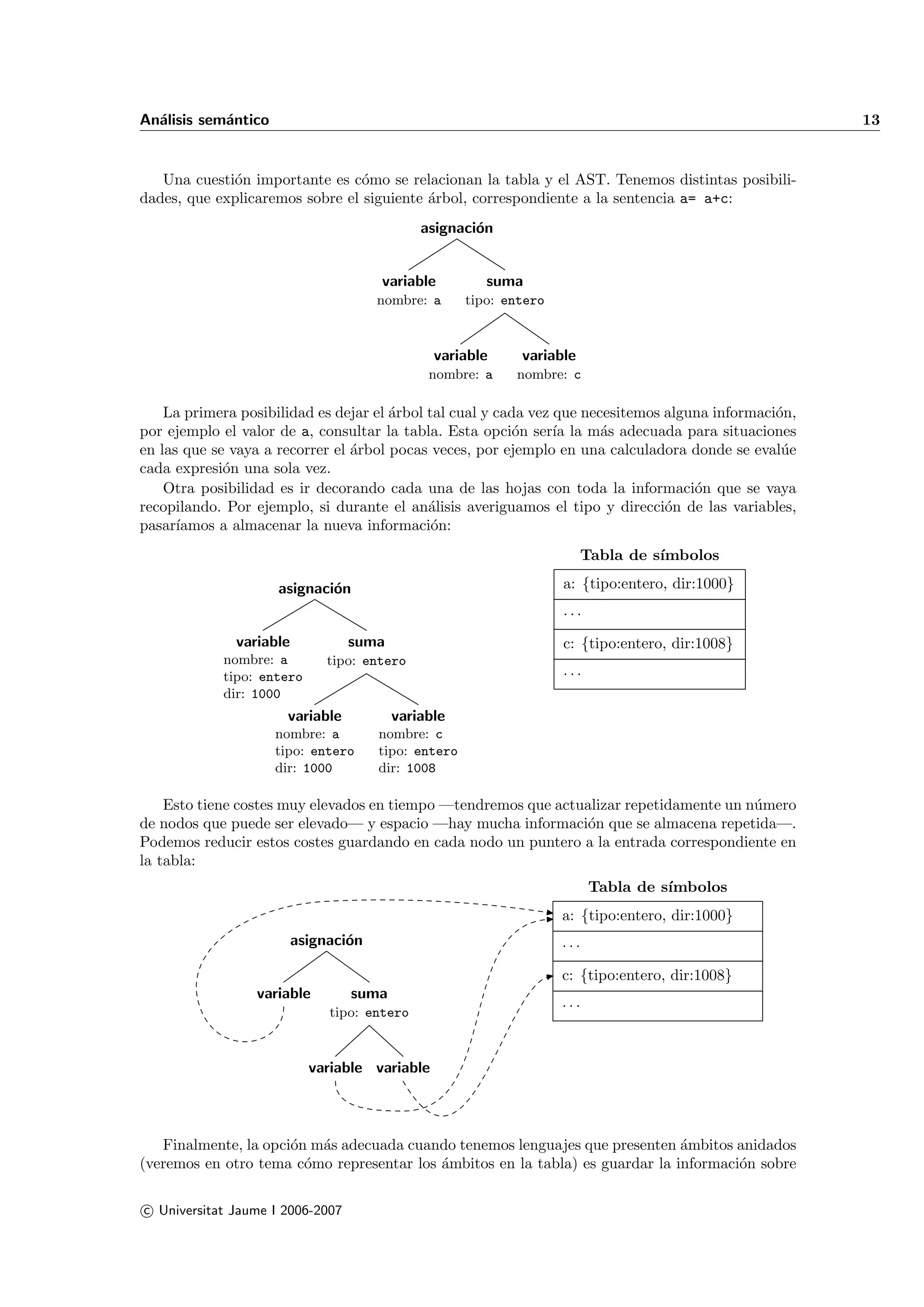
los objetos en otra estructura de datos a la que apunta tanto la tabla como los nodos del ´rbol:
a
Informaci´n objetos
o
{tipo:entero, dir:1000}
asignaci´n
o ...
{tipo:entero, dir:1008}
variable suma
...
tipo: entero
Tabla de s´
ımbolos
variable variable
a
c
...
4.2. Comprobaciones de tipos
Un aspecto importante del an´lisis sem´ntico es la comprobaci´n de los tipos de las expresiones.
a a o
Esta comprobaci´n se hace con un doble objetivo:
o
Detectar posibles errores.
Averiguar el operador o funci´n correcto en casos de sobrecarga y polimorfismo.
o
Para representar los tipos en el compilador, se emplean lo que se denominan expresiones de
tipo (ET). La definici´n de estas expresiones es generalmente recursiva. Un ejemplo ser´
o ıa:
Los tipos b´sicos: real, entero,. . . , adem´s de los tipos especiales error de tipo y ausencia de
a a
tipo (void) son ETs.
Si n1 y n2 son enteros, rango(n1 , n2 ) es una ET.
Si T es una ET, tambi´n lo es puntero(T ).
e
Si T1 y T2 son ETs, tambi´n lo es T1 → T2 .
e
Si T1 y T2 son ETs, tambi´n lo es vector(T1 , T2 ).
e
Si T1 y T2 son ETs, tambi´n lo es T1 × T2 .
e
Si T1 ,. . . ,Tk son ETs y N1 ,. . . ,Nk son nombres de campos, registro((N1 , T1 ), . . . , (Nk , Tk ))
es una ET.
Ten en cuenta que seg´n los lenguajes, estas definiciones cambian. Es m´s, los lenguajes pueden
u a
restringir qu´ expresiones realmente resultan en tipos v´lidos para los programas (por ejemplo, en
e a
Pascal no se puede definir un vector de funciones).
Algunos ejemplos de declaraciones y sus expresiones correspondientes ser´ ıan:
Declaraci´n
o Expresi´n de tipo
o
int v[10]; vector(rango(0, 9),entero)
struct { registro((a,entero), (b,real))
int a;
float b;
} st;
int *p; puntero(entero)
int f(int, char); entero × car´cter → entero
a
void f2(float); real → void

15. An´lisis sem´ntico
a a 15
4.2.1. Equivalencia de tipos
Comprobar si dos expresiones de tipo, T1 y T2 , son equivalentes es muy sencillo. Si ambas
corresponden a tipos elementales, son equivalentes si son iguales. En caso de que correspondan a
tipos estructurados, hay que comprobar si son el mismo tipo y si los componentes son equivalentes.
En muchos lenguajes se permite dar nombre a los tipos. Esto introduce una sutileza a la hora
de comprobar la equivalencia. La cuesti´n es, dada una declaraci´n como
o o
typedef int a;
typedef int b;
¿son equivalentes a y b? La respuesta depende del lenguaje (o, en casos como el Pascal, de la
implementaci´n). Existen dos criterios para la equivalencia:
o
Equivalencia de nombre: dos expresiones de tipo con nombre son equivalentes si y s´lo si tienen
o
el mismo nombre.
Equivalencia estructural: dos expresiones de tipo son equivalentes si y s´lo si tienen la misma
o
estructura.
Hay argumentos a favor de uno y otro criterio. En cualquier caso, hay que tener en cuenta que
para comprobar la equivalencia estructural ya no sirve el m´todo trivial presentado antes. En este
e
caso, puede haber ciclos, lo que obliga a utilizar algoritmos m´s complicados.
a
4.2.2. Comprobaci´n de tipos en expresiones
o
Para comprobar los tipos en las expresiones podemos utilizar un atributo que indique el tipo
de la expresi´n. Este tipo se infiere a partir de los distintos componentes de la expresi´n y de las
o o
reglas de tipos del lenguaje.
A la hora de calcular el tipo hay varias opciones: podemos calcularlo sobre la gram´tica, sobre
a
el AST o al construir el AST. En cualquier caso, puede ser util tener una funci´n similar a la de
´ o
la secci´n 3.2 que refleje las peculiaridades de los tipos del lenguaje. Por ejemplo, si tenemos tipos
o
entero y real con las reglas habituales de promoci´n, esta funci´n devolver´ los resultados seg´n
o o ıa u
esta tabla:
Primero Segundo Resultado
entero entero entero
entero real real
real entero real
real real real
otros error tipo
El c´lculo de atributos de tipo deber´ ser trivial sobre la gram´tica o sobre el AST. En cuanto
a ıa a
al c´lculo al construir el AST, se puede, por ejemplo, hacer que el constructor compruebe los tipos
a
de los componentes que recibe. En este caso, si es necesario, se puede a˜adir un nodo de promoci´n
n o
de tipos. Por ejemplo, si vamos a crear un nodo suma a partir de los ´rboles:
a
producto suma
t: entero t: real
y ,
variable num variable num
t: entero t: entero t: real t: real
nombre: a valor: 3 nombre: z valor: 3.14
podemos a˜adir un nodo intermedio para indicar la promoci´n:
n o
c Universitat Jaume I 2006-2007

16. 16 II26 Procesadores de lenguaje
suma
t: real
enteroAreal suma
t: real
producto
t: entero variable num
t: real t: real
nombre: z valor: 3.14
variable num
t: entero t: entero
nombre: a valor: 3
Respecto a la propagaci´n de los errores de tipo, hay que intentar evitar un exceso de mensajes
o
de error. Para ello se pueden utilizar distintas estrategias:
Se puede hacer que error tipo sea compatible con cualquier otro tipo.
Se puede intentar inferir cu´l ser´ el tipo en caso de no haber error. Por ejemplo: si el
a ıa
operador en que se ha detectado el error es el y-l´gico, se puede devolver como tipo el tipo
o
l´gico.
o
5. Interpretaci´n
o
La utilizaci´n del AST hace que la interpretaci´n sea bastante sencilla. Una vez lo hemos
o o
construido, tenemos dos aproximaciones para la interpretaci´n:
o
Podemos representar la entrada mediante una serie de instrucciones similares a un lenguaje
m´quina con algunas caracter´
a ısticas de alto nivel. Este es el caso, por ejemplo, de Java y el
Java bytecode. Esta aproximaci´n representa pr´cticamente una compilaci´n.
o a o
La otra alternativa es representar la entrada de manera similar al AST y recorrerlo para
ejecutar el programa.
Utilizaremos la segunda opci´n. Los nodos correspondientes a las expresiones tendr´n un m´-
o a e
todo al que llamaremos eval´a y que devolver´ el resultado de evaluar el sub´rbol correspondiente.
u a a
Por ejemplo, en el nodo de la suma tendr´ ıamos:
Objeto NodoSuma:
...
M´todo eval´a()
e u
devuelve i.eval´a() + d.eval´a(); // i y d son los hijos del nodo
u u
fin eval´a
u
...
fin NodoSuma
Aquellos nodos que representen sentencias tendr´n el m´todo interpreta. Por ejemplo, para un
a e
nodo que represente un mientras, el m´todo correspondiente ser´
e ıa:
Objeto NodoMientras:
...
M´todo interpreta()
e
mientras condici´n.eval´a()=cierto:
o u
sentencias.interpreta()
fin mientras
fin interpreta
...
fin NodoMientras

17. An´lisis sem´ntico
a a 17
Las variables se representar´ mediante entradas en una tabla (que, en casos sencillos, puede
ıan
ser la tabla de s´
ımbolos) que contenga el valor correspondiente en cada momento. Una asignaci´n o
consiste simplemente en evaluar la expresi´n correspondiente y cambiar la entrada de la tabla.
o
La ejecuci´n del programa consistir´ en una llamada al m´todo interpreta del nodo ra´ del
o a e ız
programa. Alternativamente, si hemos guardado el programa como una lista de sentencias, la
ejecuci´n consistir´ en un bucle que recorra la lista haciendo las llamadas correspondientes.
o a
L´gicamente, existen otras maneras de recorrer el ´rbol. En particular, si no lo hemos represen-
o a
tado con objetos, podemos recorrerlo mediante funciones recursivas o de manera iterativa. En este
ultimo caso, podemos emplear una pila auxiliar o ir “enhebrando” el ´rbol durante su construcci´n.
´ a o
Esta es probablemente la opci´n m´s r´pida con una implementaci´n cuidadosa, pero es tambi´n
o a a o e
la que m´s esfuerzo exige (especialmente si hay que recorrer el ´rbol en distintos ´rdenes).
a a o
6. Introducci´n a metacomp
o
Mediante metacomp se pueden traducir esquemas de traducci´n a programas Python que im-
o
plementan los correspondientes analizadores descendentes recursivos.
Un programa metacomp se divide en varias secciones. Cada secci´n se separa de la siguiente
o
por un car´cter “ %” que ocupa la primera posici´n de una l´
a o ınea. La primera secci´n contiene la
o
especificaci´n del analizador l´xico. Las secciones pares contienen c´digo de usuario. La tercera y
o e o
sucesivas secciones impares contienen el esquema de traducci´n. Es decir, un programa metacomp
o
se escribe en un fichero de texto siguiendo este formato:
Especificaci´n l´xica
o e
%
C´digo de usuario
o
%
Esquema de traducci´no
%
C´digo de usuario
o
%
Esquema de traducci´no
.
.
.
Las secciones de “c´digo de usuario” se utilizan para declarar estructuras de datos y variables,
o
definir funciones e importar m´dulos utiles para el procesador de lenguaje que estamos especifican-
o ´
do. Estos elementos deber´n codificarse en Python. La herramienta metacomp copia literalmente
a
estos fragmentos de c´digo en el programa que produce como salida.
o
6.1. Especificaci´n l´xica
o e
La especificaci´n l´xica consiste en una serie de l´
o e ıneas con tres partes cada una:
Un nombre de categor´ o la palabra None si la categor´ se omite.
ıa ıa
Un nombre de funci´n de tratamiento o None si no es necesario ning´n tratamiento.
o u
Una expresi´n regular.
o
Los analizadores l´xicos generados por metacomp dividen la entrada siguiendo la estrategia
e
avariciosa y, en caso de conflicto, prefiriendo las categor´ que aparecen en primer lugar. Por
ıas
cada lexema encontrado en la entrada se llama a la correspondiente funci´n de tratamiento, que
o
normalmente se limita a calcular alg´n atributo adicional a los tres que tienen por defecto todos
u
los componentes: lexema, nlinea y cat, que representan, respectivamente, el lexema, el n´mero de
u
l´
ınea y la etiqueta de categor´ del componente.
ıa
c Universitat Jaume I 2006-2007

18. 18 II26 Procesadores de lenguaje
Un ejemplo de especificaci´n l´xica para una calculadora sencilla ser´
o e ıa:
categor´
ıa expresi´n regular
o acciones atributos
+
num [0–9] calcular valor valor
emitir
sum [-+] copiar lexema lexema
emitir
abre ( emitir
cierra ) emitir
espacio [ t]+ omitir
nl n emitir
En metacomp, lo podemos escribir as´
ı:
num valor [0-9]+
sum None [-+]
abre None (
cierra None )
None None [ t]+
nl None n
Donde valor ser´ una funci´n como la siguiente:
ıa o
def valor(componente):
componente.v= int(componente.lexema)
No necesitamos ning´n tratamiento para sum ya que metacomp a˜ade por defecto el atributo lexema
u n
(que es el que hemos usado para calcular el valor de los enteros).
6.2. Esquema de traducci´n
o
Las secciones de esquema de traducci´n contienen las reglas de la GPDR utilizando una sintaxis
o
muy similar a la de la asignatura. Cada regla tiene una parte izquierda, un s´ımbolo ->, una parte
derecha y un punto y coma. Los no terminales se escriben marcados mediante < y >. Los terminales
tienen que coincidir con los declarados en la especificaci´n l´xica2 . Se pueden emplear los opera-
o e
dores regulares de concatenaci´n (impl´
o ıcita), disyunci´n (mediante |), opcionalidad (mediante ?),
o
clausura (mediante *) y clausura positiva (mediante +). Por ejemplo, la regla
E → T (sum T )∗
se escribir´ en metacomp as´
ıa ı:
<E> -> <T> ( sum <T> )*;
Las acciones de las reglas se escriben encerradas entre arrobas (@) y sin fin de l´ ınea entre
ellas. Para poder referirse a los terminales y no terminales, estos est´n numerados por su orden
a
de aparici´n en la parte derecha de la regla. El no terminal de la izquierda no tiene n´mero y,
o u
si no hay ambig¨edad, la primera aparici´n de cada s´
u o ımbolo no necesita n´mero. Si tenemos las
u
acciones de la regla anterior:
E → T 1 {v:= T 1 .v}
(sum T 2 {si sum.lexema= “+” entonces v:= v+ T 2 .v si no v:= v− T 2 .v fin si})∗
{ E .v:= v}
podemos escribirlas en metacomp as´
ı:
2 Existe tambi´n la posibilidad de utilizar una sintaxis especial para categor´
e ıas con un s´lo lexema, pero no lo
o
comentaremos.

19. An´lisis sem´ntico
a a 19
<E> -> <T> @v= T.v@
( sum <T>
@if sum.lexema=="+":@
@ v+= T2.v@
@else:@
@ v-= T2.v@
)*
@E.v= v@;
7. Algunas aplicaciones
Vamos a aprovechar metacomp para reescribir los ejemplos que vimos en el tema de an´lisis
a
l´xico: la suma de las columnas de un fichero con campos separados por tabuladores y la lectura
e
de ficheros de configuraci´n.
o
7.1. Ficheros organizados por columnas
La representaci´n en metacomp de la especificaci´n l´xica podr´ ser:
o o e ıa
1 numero valor [0-9]+
2 separacion None t
3 nl None n
4 None None [ ]+
La funci´n valor se define en la zona de auxiliares junto con dos funciones para tratamiento
o
de errores:
5 %
6 def valor(componente):
7 componente.v= int(componente.lexema)
8
9 def error(linea, mensaje):
10 sys.stderr.write("Error en l´nea %d: %sn" % (linea, mensaje))
ı
11 sys.exit(1)
12
13 def error_lexico(linea, cadena):
14 if len(cadena)> 1:
15 error(linea, "no he podido analizar la cadena %s." % repr(cadena))
16 else:
17 error(linea, "no he podido analizar el car´cter %s." % repr(cadena))
a
18
19 ncol= 0
La funci´n error la utilizamos para escribir mensajes gen´ricos. La funci´n error_lexico es
o e o
llamada por metacomp cuando encuentra un error l´xico. Los dos par´metros que recibe son la
e a
l´
ınea donde se ha producido el error y el car´cter o caracteres que no se han podido analizar.
a
Podemos emplear el siguiente esquema de traducci´n:o
Fichero → {suma:=0}( L´ ınea .v})∗ { Fichero .suma:= suma}
ınea nl {suma:= suma+ L´
L´
ınea → numero1 {global ncol; col:=1; si col= ncol entonces L´
ınea .v:= numero.v fin si}
(separaci´n n´mero2
o u
{col:= col+1; si col= ncol entonces L´
ınea .v:= numero2 .v fin si}
)∗
c Universitat Jaume I 2006-2007

20. 20 II26 Procesadores de lenguaje
Hemos supuesto que el s´
ımbolo inicial tiene un atributo sintetizado que leer´ el entorno. Ade-
a
m´s, la columna deseada est´ en la variable global ncol. Representamos esto en metacomp as´
a a ı:
20 %
21 <Fichero>-> @suma= 0@
22 ( <Linea> @suma+= Linea.v@ nl )*
23 @Fichero.suma= suma@ ;
24
25 <Fichero>-> error
26 @error(mc_al.linea(), "l´nea mal formada")@
ı
27 ;
28
29 <Linea>-> numero
30 @col= 1@
31 @if col== ncol:@
32 @ Linea.v= numero.v@
33 ( separacion numero
34 @col+= 1@
35 @if col== ncol:@
36 @ Linea.v= numero2.v@
37 )*
38 @if col< ncol:@
39 @ error(numero.nlinea, "no hay suficientes columnas")@
40 ;
41
La regla <Fichero>-> error nos permite capturar los errores que se produzcan durante el an´lisis.
a
Hay varias maneras de tratar los errores, pero hemos optado por abortar el programa. Hemos
utilizado mc_al, que contiene el analizador l´xico, para averiguar el n´mero de l´
e u ınea del error.
Finalmente, hemos decidido que el programa tenga un par´metro que indique qu´ columna
a e
sumar. Si no se especifica ning´n par´metro adicional, se leer´ la entrada est´ndar. En caso de que
u a a a
haya varios par´metros, se sumar´ la columna deseada de cada uno de los ficheros especificados,
a a
escribi´ndose el total. Con esto, el programa principal es:
e
42 %
43 def main():
44 global ncol
45 if len(sys.argv)== 1:
46 sys.stderr.write("Error, necesito un n´mero de columna.n")
u
47 sys.exit(1)
48 try:
49 ncol= int(sys.argv[1])
50 except:
51 sys.stderr.write("Error, n´mero de columna mal formado.n")
u
52 sys.exit(1)
53
54 if len(sys.argv)== 2:
55 A= AnalizadorSintactico(sys.stdin)
56 suma= A.Fichero.suma
57 else:
58 suma= 0
59 for arg in sys.argv[2:]:
60 try:
61 f= open(arg)
62 except:

21. An´lisis sem´ntico
a a 21
63 sys.stderr.write("Error, no he podido abrir el fichero %s.n" % arg)
64 sys.exit(1)
65 A= AnalizadorSintactico(f)
66 suma+= A.Fichero.suma
67 print "La suma es %d." % suma
Por defecto, metacomp genera una funci´n main que analiza sys.stdin. Si queremos modificar ese
o
comportamiento, debemos crear nuestra propia funci´n. Como ves, la mayor parte del c´digo se
o o
dedica a analizar posibles errores en los par´metros. La construcci´n m´s interesante est´ en las
a o a a
dos l´
ıneas que crean el analizador. La asignaci´n
o
A= AnalizadorSintactico(f)
hace que se cree un analizador que inmediatamente analizar´ el fichero f (que debe estar abierto).
a
Cuando termina el an´lisis, el objeto A tiene un atributo con el nombre del s´
a ımbolo inicial y que
tiene sus atributos sintetizados. As´ es como transmitimos el resultado.
ı
7.2. Ficheros de configuraci´n
o
Vamos ahora a programar el m´dulo de lectura de los ficheros de configuraci´n. Haremos que
o o
el resultado del an´lisis sea un diccionario en el que las claves sean las variables y los valores
a
asociados sean los le´ıdos del fichero.
El analizador l´xico se escribir´ as´
e ıa ı:
1 variable None [a-zA-Z][a-zA-Z0-9]*
2 igual None =
3 valor None [0-9]+|"[^"n]*"
4 nl None (#[^n]*)?n
5 None None [ t]+
Los unicos auxiliares que necesitamos son las funciones de tratamiento de errores:
´
6 %
7 def error(linea, mensaje):
8 sys.stderr.write("Error en l´nea %d: %sn" % (linea, mensaje))
ı
9 sys.exit(1)
10
11 def error_lexico(linea, cadena):
12 if len(cadena)> 1:
13 error(linea, "no he podido analizar la cadena %s." % repr(cadena))
14 else:
15 error(linea, "no he podido analizar el car´cter %s." % repr(cadena))
a
Nuestro esquema de traducci´n ser´:
o a
Fichero → {dic:= {}}(( L´
ınea {dic[ L´ ınea .dcha}|λ) nl)∗ { Fichero .dic:= dic}
ınea .izda]:= L´
L´
ınea → variable { L´
ınea .izda:= variable.lexema } igual valor { L´
ınea .dcha:= valor.lexema}
Pasado a metacomp:
16 %
17 <Fichero>-> @dic= {}@
18 ( (<Linea> @dic[Linea.izda]= Linea.dcha@)? nl )*
19 @Fichero.dic= dic@ ;
20
21 <Fichero>-> error
c Universitat Jaume I 2006-2007

22. 22 II26 Procesadores de lenguaje
22 @error(mc_al.linea(), "l´nea mal formada")@
ı
23 ;
24
25 <Linea>-> variable
26 @Linea.izda= variable.lexema@
27 igual valor
28 @Linea.dcha= valor.lexema@
29 ;
30
Como ves, hemos utilizado el operador de opcionalidad para representar la disyunci´n ( Linea |λ).
o
8. Resumen del tema
El analizador sem´ntico tiene dos objetivos:
a
• Hacer comprobaciones que no se hagan durante el an´lisis l´xico o sint´ctico.
a e a
• Crear una representaci´n adecuada para fases posteriores.
o
Implementaremos el an´lisis sem´ntico en dos partes:
a a
• Mediante esquemas de traducci´n dirigidos por la sintaxis.
o
• Recorriendo el AST.
Un esquema de traducci´n dirigido por la sintaxis a˜ade a las gram´ticas:
o n a
• Acciones intercaladas en las partes derechas de las reglas.
• Atributos asociados a los no terminales.
Dos tipos de atributos: heredados y sintetizados.
Las acciones deben garantizar que se eval´an correctamente los atributos.
u
Se pueden implementar los esquemas de traducci´n sobre los analizadores sint´cticos inter-
o a
pretando los atributos como par´metros y a˜adiendo el c´digo de las acciones al c´digo del
a n o o
analizador.
El c´lculo de algunos atributos y algunas comprobaciones sem´nticas son m´s f´ciles sobre
a a a a
el AST.
La tabla de s´
ımbolos se puede implementar eficientemente mediante una tabla hash.
Las comprobaciones de tipos se complican si se introducen nombres. Dos criterios:
• Equivalencia de nombre.
• Equivalencia estructural.
La interpretaci´n se puede realizar mediante recorridos del AST.
o
metacomp permite implementar c´modamente esquemas de traducci´n dirigidos por la sin-
o o
taxis.