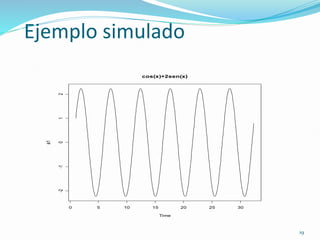
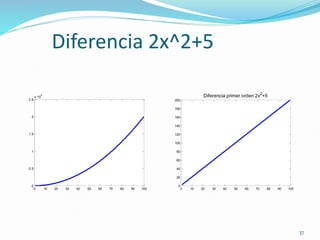
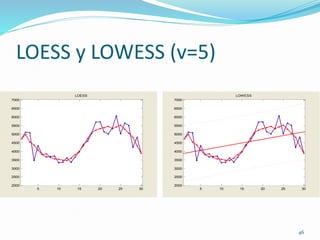
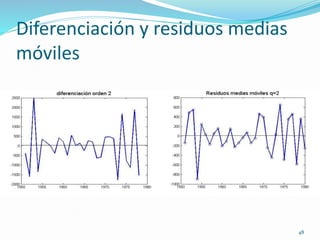
Este documento presenta los conceptos y métodos básicos para el análisis descriptivo y la descomposición de series temporales. Incluye ejemplos de detección de tendencias y estacionalidad en series de tráfico aéreo y niveles del lago Huron a través de tablas, gráficos y ANOVA. También cubre la descomposición de series en componentes de tendencia, estacionalidad y ruido mediante autocorrelaciones y diferenciación.
















![17
Ejemplo Lago Huron:
Otro modelo: t
t
t
t
t r
x
r
bx
x
1
1 791
.
0
6 7 8 9 10 11 12
6
7
8
9
10
11
12
lago[2:98]
lago[1:97]](https://image.slidesharecdn.com/clase2-230501232333-ec83a040/85/Series-de-tiempo-17-320.jpg)